1.14. Повторення незалежних випробувань. Формула Пуассона.

Розглянемо таку задачу: знайти ймовірність того, що подія відбудеться 40 разів у 100 випробуваннях, якщо ймовірність появи події у кожному випробуванні .

Згідно з формулою Бернуллі матимемо:

.

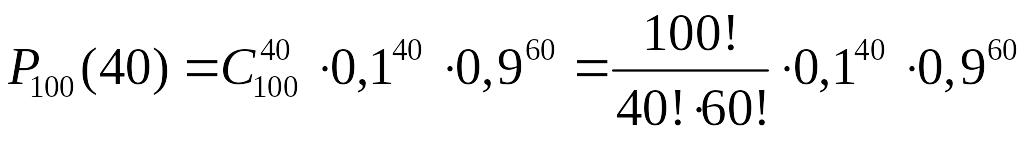Звідси видно, що ми змушені мати справу з величезними числами, практично провести такі обчислення дуже складно, до того ж у процесі обчислення накопичуються похибки, внаслідок яких отриманий результат може значно відрізнятися від правильного.

Таким чином при великих значеннях формулою Бернуллі користуватися практично неможливо, і у таких випадках користуються іншими формулами. Однією з таких формул є формула Пуассона⁴.

Припустимо, що ймовірність дуже мала, . І крім того, добуток зберігає постійне значення : . Знайдемо ймовірність . Оскільки , то це буде означати, що , тобто подія трапляється дуже рідко. Скористаємось спочатку формулою Бернуллі:

.

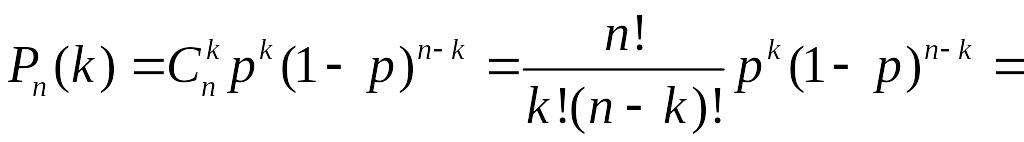
Оскільки , то . Отже:

.

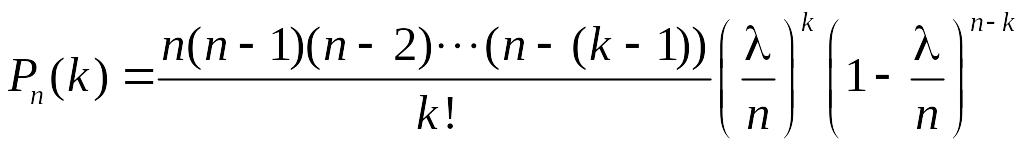Враховуючи, що приймає дуже великі значення, замість знайдемо .

.

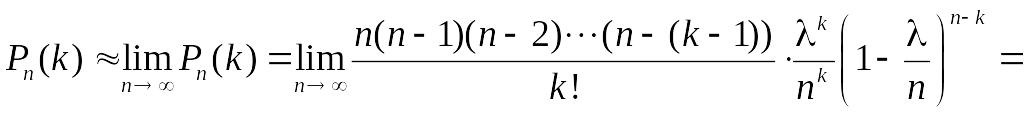
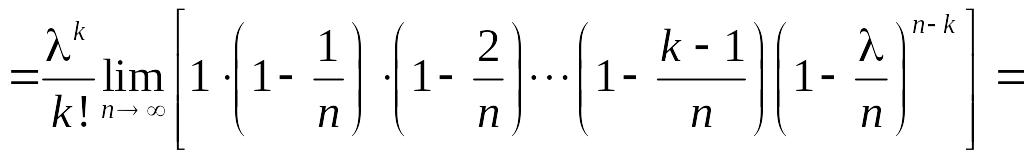
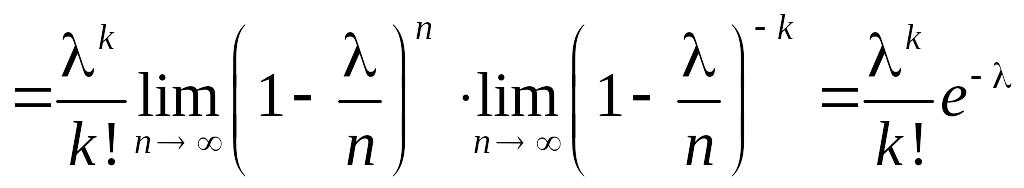Таким чином:

.

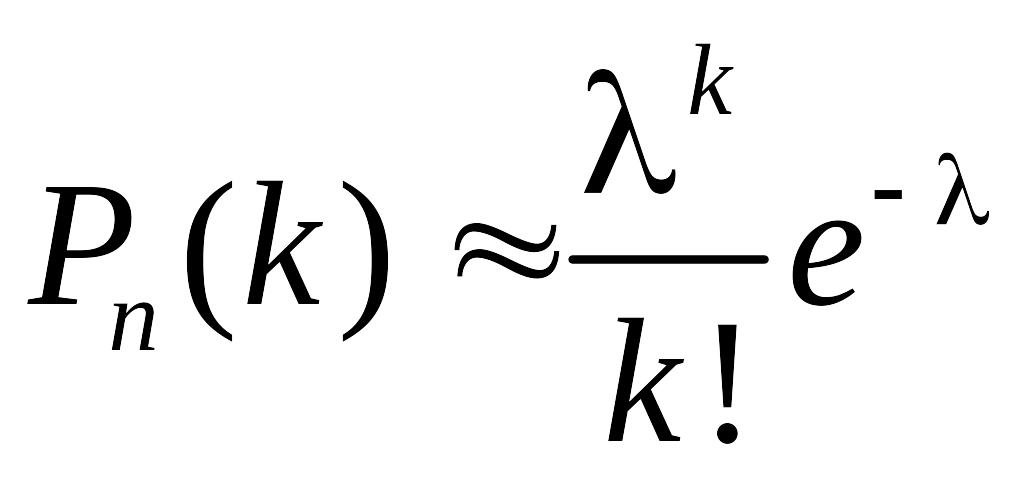Це й є формула Пуассона.

Приклади.

1. Станок-автомат штампує деталі. Ймовірність того, що деталь буде з дефектом, дорівнює 0,01. Знайти ймовірність того, що серед 200 деталей буде рівно 4 з дефектом.

Маємо: .

.

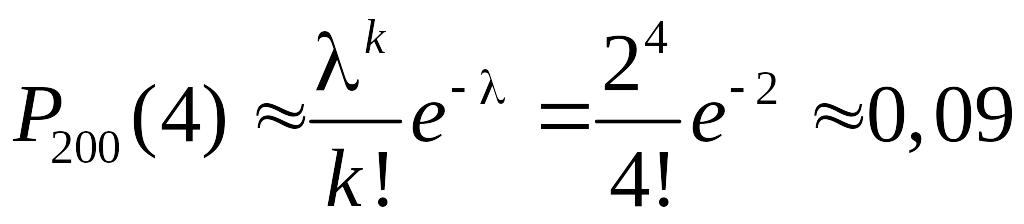2. Здійснюється залп з 100 гармат. Ймовірність влучання в ціль для кожної з гармат дорівнює 0,03. Знайти ймовірність того, що буде не менш, ніж 2 влучання в ціль.

Перейдемо до ймовірності протилежної події – вона полягає в тому, що відбудеться менше 2 влучень, тобто або жодного влучання (подія ), або одне влучання (подія ).

Маємо: .

, .

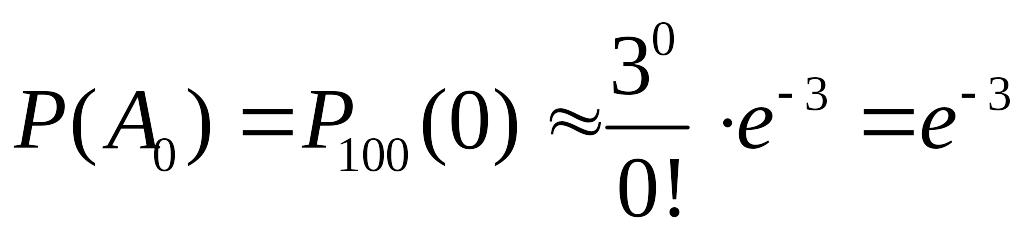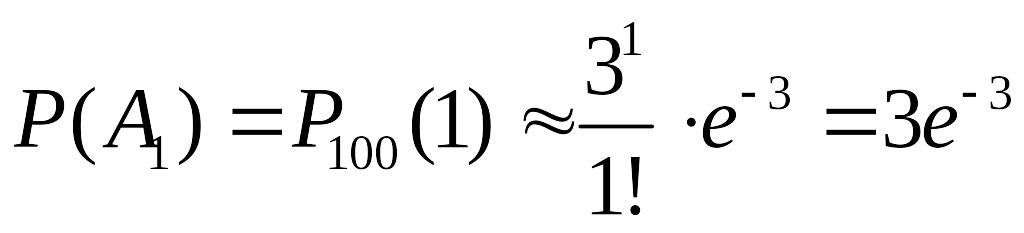Події і несумісні, отже

.

Таким чином, шукана ймовірність:

.

1.15. Повторення незалежних випробувань. Локальна теорема Муавра – Лапласа.

Як відмічалося, формула Пуассона використовується при великих значеннях за умов, що . Якщо ці умови не виконано, то для обчислення ймовірності при великих користуються іншою наближеною формулою, яку ми наводимо без доведення:

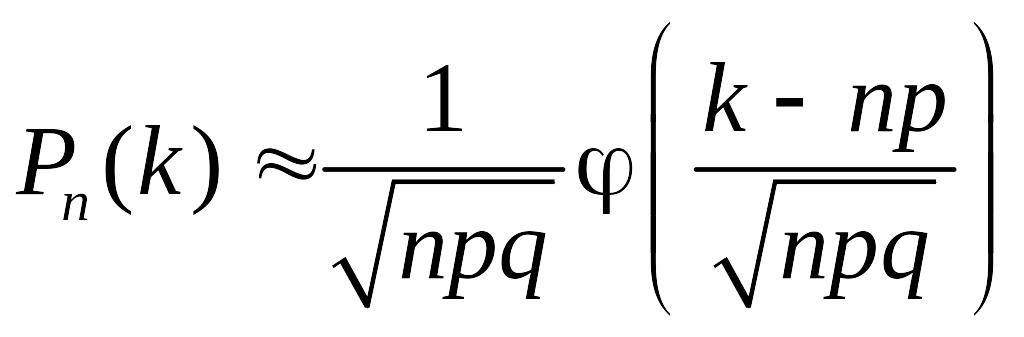, (*) де функція

.

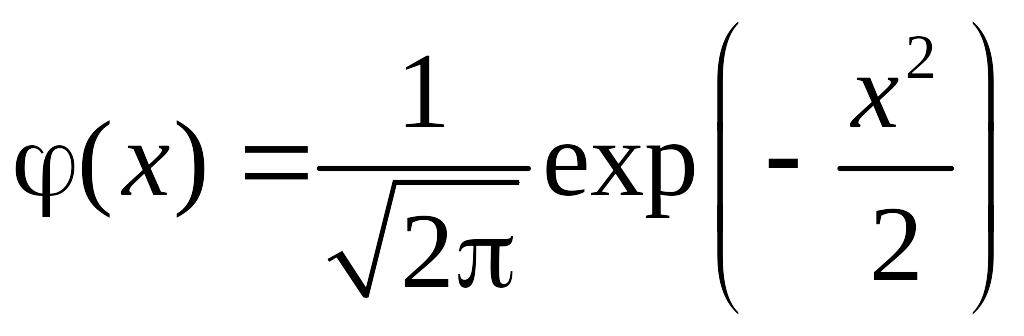Дослідимо деякі важливі властивості цієї функції. Ця функція, очевидно, додатна: ; парна: . Далі , причому прямування до нуля значень функції відбувається досить швидко – на практиці вже при значення функції можна вважати нулем.

Знайдемо проміжки зростання та спадання та точки екстремуму функції :

.

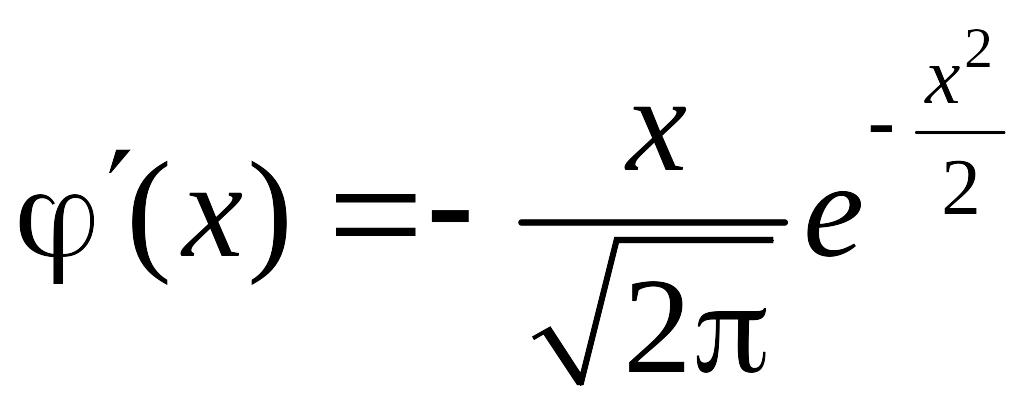Звідси видно, що при , при , при . Тобто при функція зростає, при функція спадає, і в точці має максимум, який дорівнює .

Знайдемо проміжки опуклості та вгнутості та точки перегину функції :

.

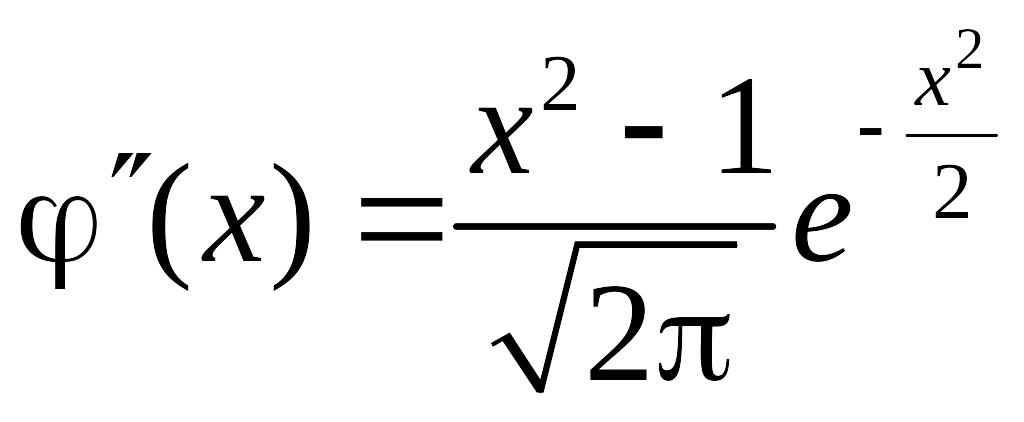Звідси видно, що при , при , при . Тобто проміжки є проміжками вгнутості, а проміжок є проміжком опуклості функції . Схематичний графік функції наведено на рис. 10.

Рис. 10.

Функція затабульована, тобто складено детальні таблиці її значень. На практиці для знаходження значень функції користуються саме цими таблицями. Таку таблицю наведено у Додатку (Таблиця 1). В ній наведено значення функції для сітки значень від 0 до 4. При користуються властивістю парності цієї функції, а при покладається .

Формула (*) називається локальною теоремою Муавра – Лапласа⁵, а функція – диференціальною функцією Лапласа.

Приклади.

1. Ймовірність влучення в ціль при кожному пострілі дорівнює 0,8. Знайти ймовірність того, що при 100 пострілах буде рівно 75 влучень.

За умовою , . Помітимо, що тут велике, а умови не виконано, тому формули Бернуллі та Пуассона ми не можемо використати. Скористаємось локальною теоремою Муавра – Лапласа. Маємо:

.

.

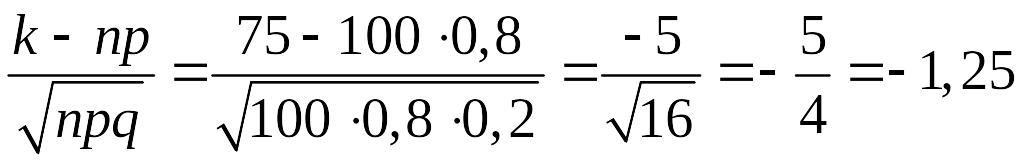2. Монета кидається 4 рази. Знайти ймовірність того, що рівно 2 рази з’явиться «герб».

Хоча тут не є великим ( ) , спробуємо все ж скористатися локальною теоремою Муавра – Лапласа. Маємо: ,

,

.

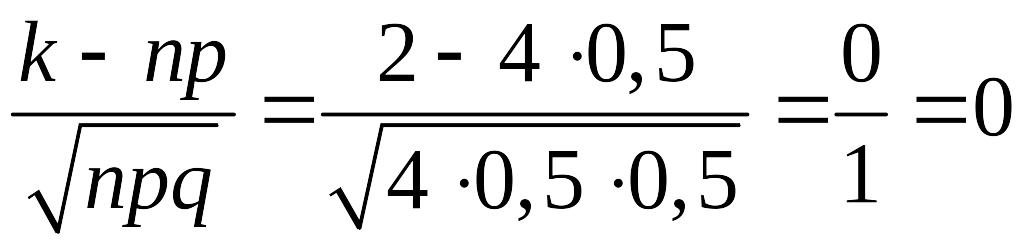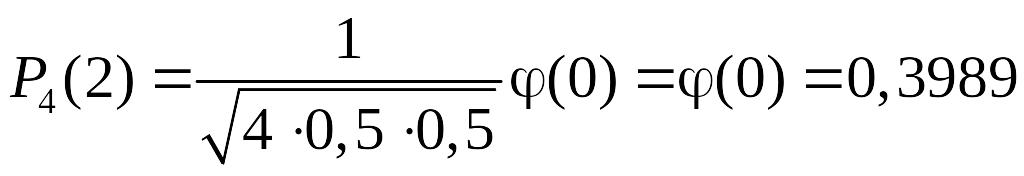А тепер розв’яжемо цю задачу за формулою Бернуллі:

.

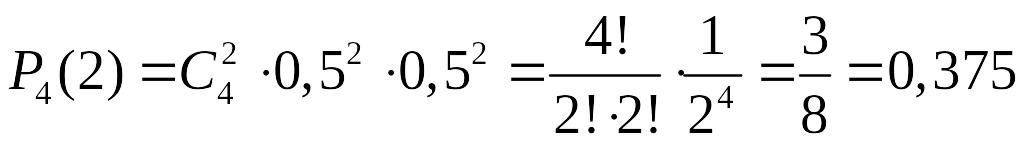Ми бачимо значну розбіжність в результатах. Це відбулося внаслідок того, що не є досить великим числом, тому локальна теорема Муавра – Лапласа дає помітну похибку.