1.12. Формули Байєса.

Розглянемо таку задачу. Є дві урни з кулями, в кожній урні по 10 куль. В першій 9 білих куль і тільки одна чорна, а в другій навпаки – 1 біла і 9 чорних. Навмання вибирається одна з двох урн. Зрозуміло тоді, що ймовірність вибору кожної урни одна й та ж і дорівнює . Тепер припустимо, що з тієї урни, що вибрано, також навмання вибирається одна куля, і ця куля з’являється білою. Тоді питання: з якої урни ймовірніше було взято цю кулю? Зрозуміло, що з першої, адже в ній значно більше можливостей для появи білої кулі. Тобто виходить, що коли ми дістали з урни кулю, і вона з’явилася білою, то ймовірність того, що ми взяли першу урну, не , як раніше, а вже інша. Таким чином, якщо – подія, що з вибраної урни з’явилася біла куля, – гіпотеза, яка полягає в тому, що було вибрано першу урну, – гіпотеза, яка полягає в тому, що було вибрано другу урну, то ми можемо стверджувати, що ймовірності гіпотез, які обчислено до здійснення події , і ймовірності тих самих гіпотез, які обчислено після здійснення події – різні. Отже виникає задача обчислення саме других ймовірностей.

Сформулюємо тепер задачу в загальному випадку. Нехай подія може відбутися при здійсненні однієї з гіпотез . Ймовірності , , … , цих гіпотез назвемо апріорними (від латинського a priori – до випробування). Припустимо, що проведено випробування, внаслідок якого відбулася подія . Треба знайти умовні ймовірності , , … , , які ми назвемо апостеріорними (від латинського a posteriori – після випробування).

Знайдемо спочатку . За формулою для ймовірності добутку подій знайдемо:

, звідки

.

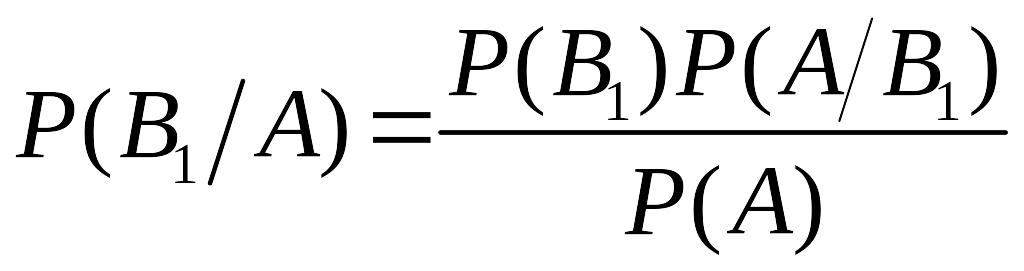Обчислюючи тепер за формулою повної ймовірності, дістанемо:

.

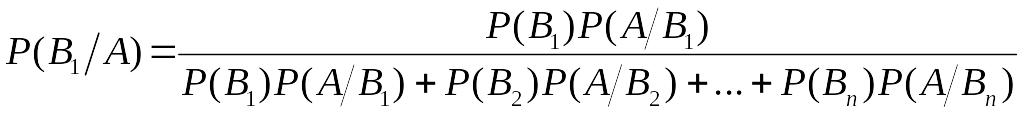Аналогічно отримуються формули і для інших апостеріорних ймовірностей. Таким чином маємо:

.

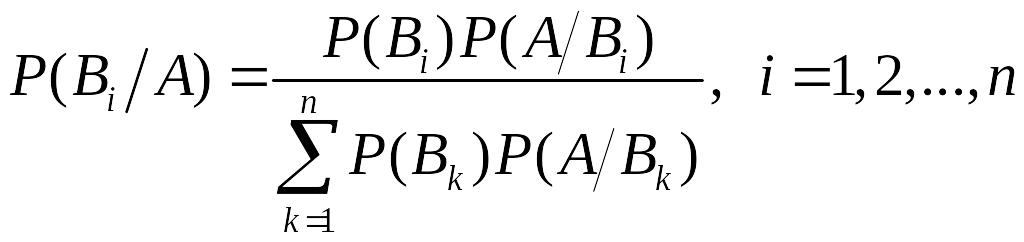Ці формули називаються формулами Байєса¹ .

Приклад. Виріб перевіряється на стандартність одним з двох контролерів. Ймовірність того, що виріб потрапить до 1-го контролера, дорівнює 0,55, а до 2-го – 0,45. Ймовірність того, що стандартний виріб буде визнано стандартним 1-м контролером, дорівнює 0,90, а 2-м – 0,98. Стандартний виріб після перевірки було визнано стандартним. Знайти ймовірність того, що цей виріб перевіряв 2-й контролер.

Нехай подія – виріб визнано стандартним, гіпотеза – виріб перевіряв 1-й контролер, гіпотеза – виріб перевіряв 2-й контролер. Тоді треба знайти . Згідно з формулами Байєса маємо:

1.13. Повторення незалежних випробувань. Формула Бернуллі.

Припустимо, що ми проводимо серію випробувань, у кожному з яких може відбутися подія . Причому ймовірність появи події в кожному випробування не залежить від наслідків інших випробувань. Такі випробування називають незалежними відносно події .

Припустимо також, що у кожному з випробувань ймовірність появи події одна й та ж (хоча, взагалі кажучи, у кожному випробуванні ця ймовірність може бути своя). Позначимо цю ймовірність як . Тоді ймовірність того, що подія не відбудеться, у кожному з випробувань теж одна й та ж і дорівнює .

Поставимо задачу: знайти ймовірність того, що при випробуваннях подія відбудеться рівно разів. Позначимо цю ймовірність як . Наприклад означає ймовірність того, що в 5 випробуваннях подія відбудеться рівно 3 рази.

Розглянемо для спрощення спочатку саме цю ймовірність. Нехай – подія, що полягає в тому, що подія відбулася у -му випробуванні. Тоді подія, що нас цікавить, може бути подана у вигляді:

.

Таким чином отримали суму 10 подій. Помітимо, що число 10 виникло невипадково – це не що інше, як . Оскільки події незалежні в сукупності, і , , то ймовірність, наприклад, події дорівнює:

.

Така ж сама ймовірність і у всієї решти з вищеозначених 10 подій. Ці події є, очевидно, попарно несумісними, тому ймовірність їх суми дорівнює сумі їх ймовірностей, отже:

.

Аналогічно розглядається і загальний випадок, внаслідок чого отримуємо формулу:

.

Ця формула називається формулою Бернуллі².

Приклади.

1. Стрілок 7 разів стріляє по цілі, причому кожного разу він влучає в ціль з ймовірністю 0,8. Знайти ймовірність того, що він влучить в ціль рівно 5 разів.

Згідно з формулою Бернуллі маємо:

.

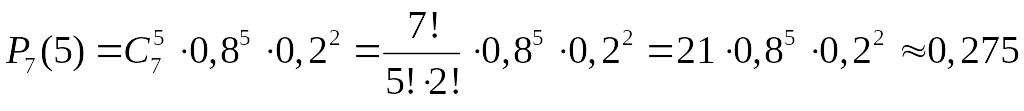2. Дві рівносильні хокейні команди НХЛ проводять серію матчів на Кубок Стенлі. Що більш ймовірно для кожної з них – виграти два матчі з чотирьох, або три матчі з шести? Нічиї, згідно з правилами цих змагань, виключено.

Оскільки команди рівносильні, то кожна з них виграє матч з ймовірністю . Отже ймовірність виграти два матчі з чотирьох:

.

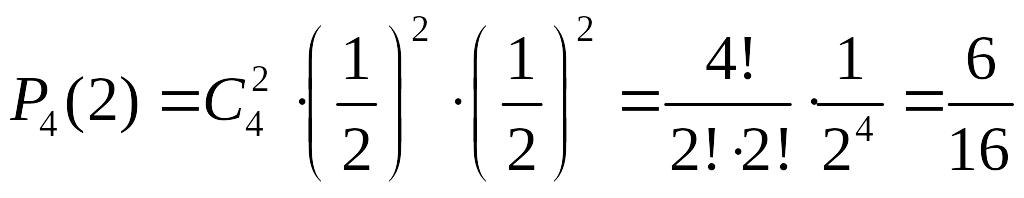А ймовірність виграти три матчі з шести:

.

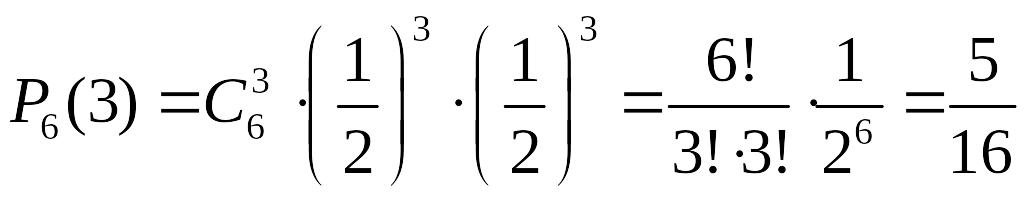Оскільки , то більш ймовірно виграти 2 матчі з 4-х, ніж 3 з 6.

3. Монету кидають 5 разів. Знайти ймовірність того, що «герб» випаде не менш, ніж два рази.

Нехай подія – «герб» випав рівно разів. Тоді подія, що нас цікавить є . А протилежна їй подія – . Знайдемо ймовірність саме цієї події:

.

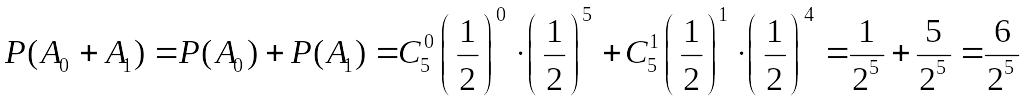Отже шукана ймовірність:

.

4. На відрізок довжиною навмання кинуто 6 точок. Знайти ймовірність того, що 4 точки опиняться від точки на відстані менш, ніж , а 2 точки – на відстані більшій, ніж . Припускається, що ймовірність потрапляння точки на відрізок пропорційна довжині цього відрізку і не залежить від його розташування.

Нехай точка лежить від точки на відстані . Тоді вказані 4 точки мають опинитися на відрізку (рис. 9).

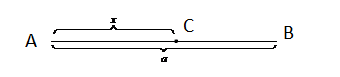
Рис. 9.

Знайдемо ймовірність потрапляння однієї точки на відрізок , якщо вона обов’язково потрапляє на відрізок . Згідно з формулою геометричної ймовірності:

.

Тепер згідно з формулою Бернуллі маємо:

.

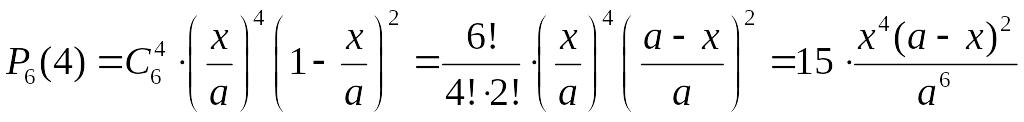Зокрема, якщо, наприклад, , то

.

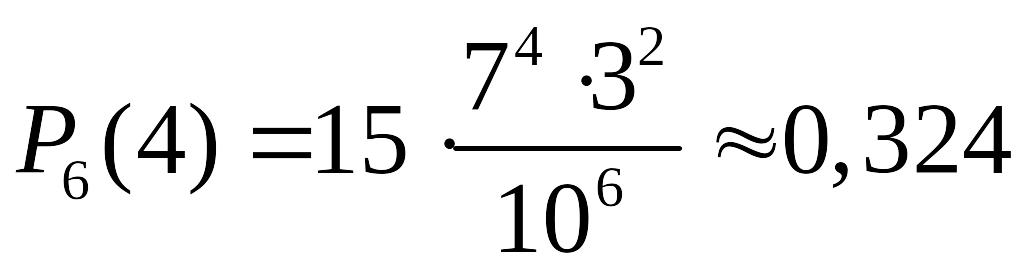5. Задача Банаха³. Математик, що палить, носить з собою 2 коробки сірників. Кожного разу, коли він хоче дістати сірник, він навмання дістає одну з коробок. Знайти ймовірність того, що, коли він першого разу витягне порожню коробку, у другій коробці залишиться рівно сірників, якщо початково у кожній коробці було по сірників .

Позначимо як подію, яка полягає в тому, що сірник дістається з тієї коробки, яка має залишитися порожньою. Ймовірність цієї події в одному випробуванні: . Для того, щоб коробка залишилася порожньою, подія має відбутися разів. А оскільки у другій коробці при цьому залишилося сірників, то це означає, що відбулося рівно діставань сірника. Отже нас цікавить . Згідно з формулою Бернуллі:

.

Якщо, зокрема, , то ця ймовірність дорівнює .