1.10. Задачі на обчислення ймовірностей суми та добутку подій.

Задача 1. В ящику лежать 10 деталей, з яких 4 стандартні. Навмання беруть 6 деталей. Знайти ймовірність того, що серед цих 6 не більше 2 стандартних.

Нехай – подія, яка полягає в тому, що серед 6 деталей, що взято, рівно стандартних. Тоді подія, що нас цікавить: . Події несумісні, отже

.

Маємо (див. задачу про вибірку, п. 1.5):

,

,

.

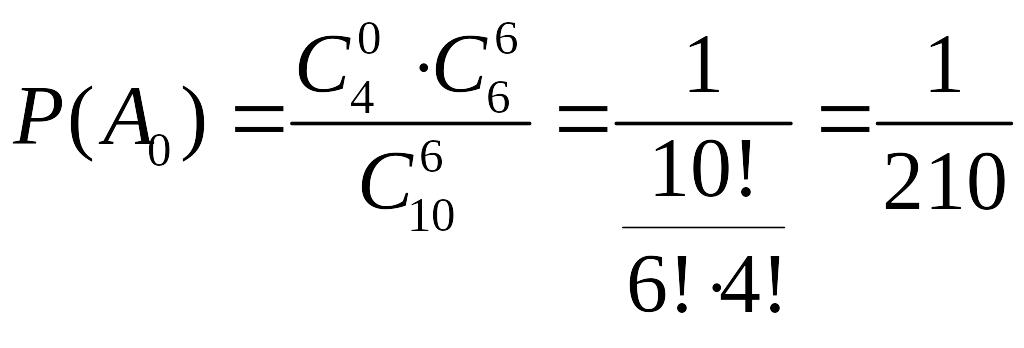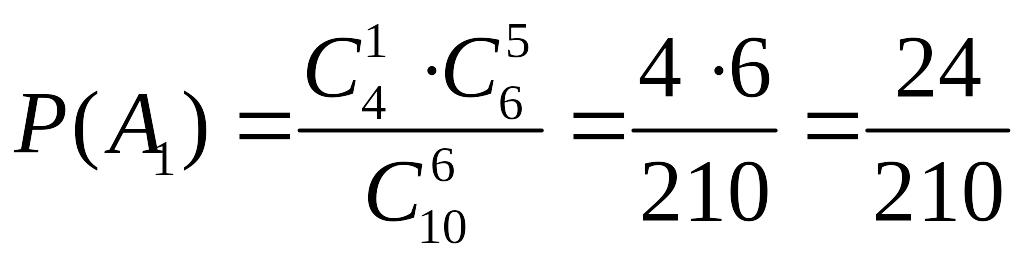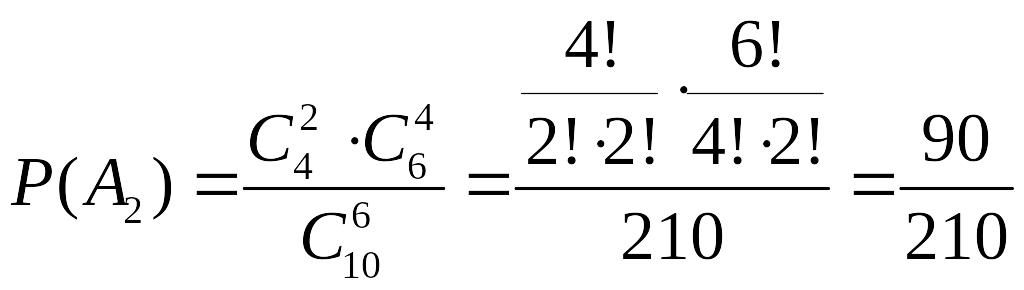Отже

.

Задача 2. В умовах попередньої задачі знайти ймовірність того, що серед 6 деталей, що взято, хоча б одна стандартна.

Очевидно, цього разу нас цікавить подія . І тоді нам треба обчислювати ймовірність суми 6 подій. Але можна зробити інакше. Розглянемо протилежну подію . Очевидно, що (серед 6 деталей, що взято, нема жодної стандартної). Отже

.

Задача 3. Студент вивчив 20 питань з 25, що їх є у програмі заліку. Викладач приймає залік за наступною схемою. Студенту задається питання. Якщо він на нього відповідає правильно, то отримує залік. Якщо правильної відповіді нема, то задається ще одне питання. Якщо на друге питання студент дає правильну відповідь, то отримує залік, а у протилежному випадку – незалік. Знайти ймовірність того, що студент здасть залік.

Нехай подія – студент відповів на перше питання, подія – студент відповів на друге питання. Тоді подія, що полягає в тому, що залік буде отримано, еквівалента події . Події і несумісні, а події і залежні, отже

.

Задача 4. У скриньці є 10 кульок з номерами від 1 до 10. Навмання одна за одною дістаються 3 кульки та назад до скриньки не повертаються. Знайти ймовірність того, що послідовно з’являться кульки з номерами 1, 4, 7.

Нехай подія – перша кулька має номер 1, подія – друга кулька має номер 4, подія – третя кулька має номер 7. Тоді нас цікавить ймовірність події . Маємо:

.

Задача 5. Два стрілка стріляють по одному разу в одну ціль. Перший стрілок влучає в ціль з ймовірністю 0,7, а другий – з ймовірністю 0,9. Знайти ймовірність наступних подій:

– влучили обидва стрілки;

– влучив тільки перший стрілок;

– влучив тільки другий стрілок;

– влучив тільки один стрілок;

– влучив хоча б один стрілок;

– жоден стрілок не влучив.

Нехай подія – влучив перший стрілок, подія – влучив другий стрілок. За умовою: , . Події і сумісні та незалежні. Тому маємо:

;

;

;

;

;

.

Зауважимо, що події і є взаємно протилежними, тому можна було б знайти також за формулою: .

1.11. Формула повної ймовірності.

Розглянемо таку задачу. Нехай для перевірки на якість виріб потрапляє з рівними ймовірностями до одного з двох експертів. А експерти різні за своїми здібностями; і вони по-різному ставляться до своїх обов’язків. Тому ймовірності, що вони визнають виріб якісним, різні. Ймовірність того, що перший експерт визнає виріб якісним, дорівнює 0,4, а відповідна ймовірність для другого експерта – 0,8. Знайти ймовірність того, що виріб буде визнано якісним.

Очевидно, що якби ми наперед знали, до якого саме з двох експертів потрапить виріб, ми б шукану ймовірність одразу ж вказали б – її задано в умові задачі. Але особливістю задачі є як раз те, що ми не знаємо завчасно, який саме експерт буде перевіряти виріб. І ми маємо розв’язувати задачу, так кажучи, в умовах невизначеності. Саме таким ситуаціям і присвячено цей параграф.

Введемо наступне поняття.

Означення. Кажуть, що події утворюють повну групу, якщо вони попарно несумісні, але внаслідок випробування хоча б одна з цих подій обов’язково відбудеться.

З означення випливає, що події несумісні, і, крім того, . Отже

.

Тобто сума ймовірностей подій, що утворюють повну групу, дорівнює одиниці. Фактично внаслідок випробування відбувається не хоча б одна, а точно одна з цих подій. Можна сказати, що події, які утворюють повну групу, це є повний перелік всіх можливих, попарно несумісних наслідків випробування.

Приклад. В ящику 10 куль – 5 білих, 3 чорних та 2 червоних. Навмання дістається одна куля. Події – ця куля біла, – ця куля чорна, – ця куля червона, утворюють повну групу. Дійсно, ці події попарно не сумісні (кожна з куль тільки одного кольору), але внаслідок випробування точно одна з них обов’язково відбудеться (куля, яку дістали, обов’язково буде або білою, або чорною, або червоною). Маємо: .

Нехай деяка подія може відбутися при здійсненні однієї з подій , які утворюють повну групу. Треба знайти ймовірність події , якщо завчасно невідомо, яка саме з подій відбулася. Тобто знайти так звану повну ймовірність події .

Назвемо події гіпотезами. За умови подія може відбутися, якщо здійсниться одна з цих подій. Іншими словами поява події означає здійснення однієї з несумісних подій . Маємо:

.

Отже дістали формулу:

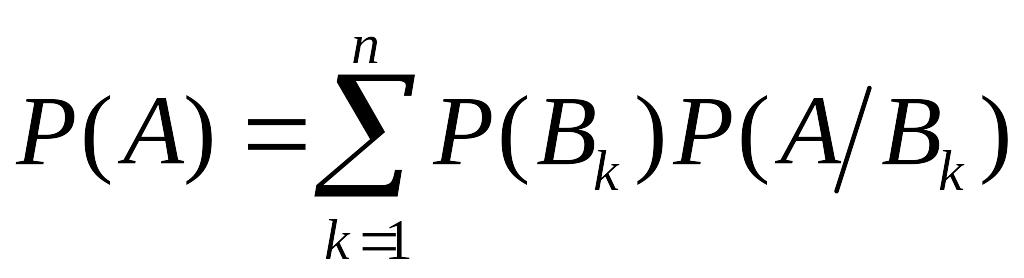, яка називається формулою повної ймовірності.

Розглянемо приклади.

Приклад 1. В двох ящиках є кулі. У першому ящику 3 білих та 5 чорних куль, у другому – 6 білих та 7 чорних. З першого ящику навмання дістали одну кулю і переклали в другий ящик, після чого з другого ящика також навмання вийняли одну кулю. Знайти ймовірність того, що ця куля біла.

Введемо гіпотези: – з першого ящика переклали білу кулю, – з першого ящика переклали чорну кулю. Знаходимо: , . Нехай подія – з другого ящика вийнято білу кулю. Тоді , . Отже за формулою повної ймовірності:

.

Приклад 2. На склад поступає продукція з 3-х заводів. 30% продукції йде з першого заводу, серед цієї продукції 3% браку; 20% продукції йде з другого заводу, серед цієї продукції 5% браку; 50% продукції йде з третього заводу, серед цієї продукції 1% браку. Зі складу навмання береться один виріб. Знайти ймовірність того, що він доброякісний.

Нехай подія – взятий виріб доброякісний. Введемо гіпотези: – цей виріб з 1-го заводу, – цей виріб з 2-го заводу, – цей виріб з 3-го заводу. За умовою: , , . Далі: , , . Згідно з формулою повної ймовірності:

.