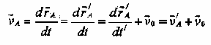- •1.Определение положения точки в пространстве. Вектор перемещения.
- •2. Вектор скорости. Вектор ускорения. Тангенциальное и нормальное ускорение
- •3.Кинематика твердого тела. Число степеней свободы. Поступательное движение твердого тела.
- •Вращательное движение твердого тела.
- •5.Движение отдельных точек вращающегося твердого тела.
- •6.Плоское движение твердого тела
- •7.Сила. Сложение сил и разложение силы на составляющие. Проекции силы на плоскость и ось.
- •8.Статическое и динамическое проявление сил. Законы Ньютона. Принцип независимости действия сил.
- •10.Основной закон динамики
- •12.Основной закон динамики системы материальных точек.
- •13.Уравнения моментов для системы материальных точек относительно произвольного центра, произвольной оси
- •14.Основной закон динамики тела переменной массы (уравнение Мещерского)
- •15.Первое и второе соотношение Циолковского.
- •15.Первое и второе соотношение Циолковского.(продолжение1)
- •16.Относительность механического движения. Галилеевы преобразования координат и закон сложения скоростей.
- •17.Постулаты Эйнштейна. "Радиолокационный" метод (метод коэффициента "k ").
- •17.(Продолжение)Постулаты Эйнштейна. "Радиолокационный" метод (метод коэффициента "k ").
- •18.Замедление" хода времени. Относительная скорость.
- •19.Сравнение поперечных размеров тел. Эффект "сокращения" длин.
- •19.Сравнение поперечных размеров тел. Эффект "сокращения" длин.(продолжение)
- •20. Преобразования Лоренца. Интервал. Инвариантность интервала.
- •Релятивистская масса, релятивистский импульс. Релятивистское уравнение движения.
- •Релятивистская масса, релятивистский импульс.
- •23.Неинерциальные системы отсчёта. Силы инерции. Силы инерции во вращающихся системах отсчета. Силы инерции Кориолиса
- •23.Силы трения. Сухое трение. Силы трения качения
- •23.Силы трения. Сухое трение. Силы трения качения.Силы трения скольжения.(продолжение)
- •24.Вязкое трение. Движение тел в сопротивляющейся среде.
- •25.Упругие силы. Продольное сжатие и растяжение. Закон Гука
- •26.Деформация сдвига и кручения.
- •27.Закон всемирного тяготения.
- •28. Потенциальная энергия гравитационного взаимодействия, гравитационный потенциал. Связь напряжённости и потенциала поля.
- •29.Работа и энергия. Работа силы тяжести. Работа упругих сил
- •30.Работа и кинетическая энергии. Потенциальная энергия. Закон сохранения энергии
- •31. Момент инерции твёрдого тела. Теорема Штейнера. Моменты инерции тел простой формы
- •Вращательное движение
- •34. Гироскопы. Прецессия волчка.
- •Давление покоящейся жидкости
- •Уравнение гидростатики Эйлера.
- •. Уравнение поверхности уровня.
- •Закон Паскаля
- •Сообщающиеся сосуды, заполненные однородной жидкостью.
- •Закон Архимеда.
- •Механика движущихся жидкостей. Расход жидкости. Уравнение неразрывности струи жидкости
- •Определения
- •Уравнение Бернулли. Формула Торричелли.
- •Примеры применения закона бернулли формула торичелли
- •Ламинарное и турбулентное течение жидкости. Число Рейнольдса.
- •43.Колебательное движение. Характеристики колебаний.
- •44.Собственные колебания
- •45. Затухающие колебания.
- •48.Геометрическое представление колебаний
- •49.Сложение одинаково направленных колебаний. Частоты складываемых колебаний одинаковы
- •50.Сложение одинаково направ. Колебаний. Частоты складываемых колебаний различны, одинаковы амплитуды и начальные фазы.
- •51.Сложение взаимно перпендикулярных колебаний.
- •53.Б) Колебания пилообразной формы
- •54.В) Колебания треугольной формы
15.Первое и второе соотношение Циолковского.(продолжение1)
Второе соотношение Циолковского
В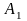
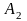 торое
соотношение Циолковского определяет
максимально возможный к.п.д. ракетного
двигателя. По-прежнему считаем, что
ракета движется вне силовых полей, а
относительная скорость продуктов
сгорания топлива постоянна. Кроме того,
полагаем, что потерями на нагрев корпуса
ракеты и на излучение можно пренебречь.
При таких предположениях работа двигателя
определяется изменением кинетической
энергии системы «ракета ― отделившиеся
продукты сгорания топлива». При этом
полезная работа определяется
изменением кинетической энергии только
корпуса ракеты, а вся затраченная работа
― изменением кинетической энергии
всей системы.
торое
соотношение Циолковского определяет
максимально возможный к.п.д. ракетного
двигателя. По-прежнему считаем, что
ракета движется вне силовых полей, а
относительная скорость продуктов
сгорания топлива постоянна. Кроме того,
полагаем, что потерями на нагрев корпуса
ракеты и на излучение можно пренебречь.
При таких предположениях работа двигателя
определяется изменением кинетической
энергии системы «ракета ― отделившиеся
продукты сгорания топлива». При этом
полезная работа определяется
изменением кинетической энергии только
корпуса ракеты, а вся затраченная работа
― изменением кинетической энергии
всей системы.
П
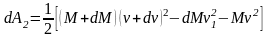 оложим,
что в момент времени t
масса ракеты была М, а скорость её .
В момент времени t+dt
система состояла из одного тела массой
M+dM,
двигавшегося со скоростью
оложим,
что в момент времени t
масса ракеты была М, а скорость её .
В момент времени t+dt
система состояла из одного тела массой
M+dM,
двигавшегося со скоростью
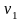 d,
и отделившихся продуктов сгорания
массы –dM,
двигавшихся со скоростью .
d,
и отделившихся продуктов сгорания
массы –dM,
двигавшихся со скоростью .
Полная работа, совершённая двигателем за промежуток времени dt, равна:
Пренебрегая величинами второго и третьего порядка малости, получим:
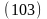
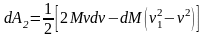
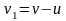 Абсолютная
скорость продуктов сгорания топлива
связана с относительной соотношением:
Абсолютная
скорость продуктов сгорания топлива
связана с относительной соотношением:
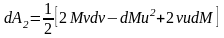
С учётом этого:
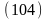
И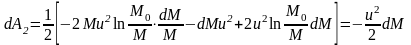 спользуя
соотношение Циолковского и полагая в
нём, что скорость ракеты в начале
активного участка траектории равна
нулю, последнее соотношение приведём
к одной переменной:
спользуя
соотношение Циолковского и полагая в
нём, что скорость ракеты в начале
активного участка траектории равна
нулю, последнее соотношение приведём
к одной переменной:
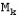
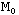
Интегрируя это равенство в пределах изменения массы ракеты (от до ), получим значение полной работы, совершённой двигателем:
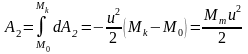
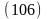
(продолжение 2) 15.Первое и второе соотношение Циолковского.
Полезная работа, совершённая двигателем за промежуток времени dt, равна:
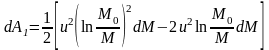
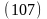
Используя 1-е соотношение Циолковского, последнее равенство можно записать в виде:
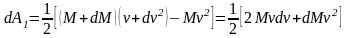
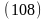
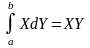
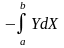
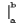 Это дифференциальное
выражение удобно интегрировать методом
интегрирования «по частям», согласно
которому:
Это дифференциальное
выражение удобно интегрировать методом
интегрирования «по частям», согласно
которому:
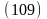
П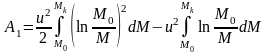
 олезная
работа на всём активном участке траектории
равна:
олезная
работа на всём активном участке траектории
равна:
Первый из интегралов интегрируем «по частям», полагая:
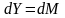
Тогда:
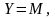
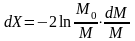
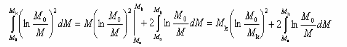
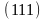 Согласно (109):
Согласно (109):
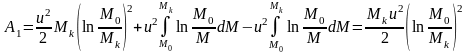
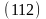 Подставив это
значение в (110) получим:
Подставив это
значение в (110) получим:
П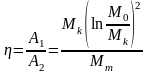 о
определению коэффициент полезного
действия ракетного двигателя равен:
о
определению коэффициент полезного
действия ракетного двигателя равен:
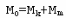
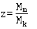
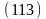
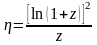
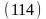 Учитывая, что
и , запишем окончательный
вид второго соотношения Циолковского:
Учитывая, что
и , запишем окончательный
вид второго соотношения Циолковского:
16.Относительность механического движения. Галилеевы преобразования координат и закон сложения скоростей.
Относительность механического движения.
Покой и движение тел относительны и определяются выбором тела отсчета (системы отсчета). Например, сидящий в вагоне движущегося поезда пассажир покоится относительно вагона и движется относительно полотна дороги.
Абсолютным называется движение тела относительно системы, условно принятой за неподвижную.
Система, совершающая движение относительно неподвижной системы, называется движущейся или подвижной.
Относительным называется движение тела относительно подвижной системы. Переносным называется движение подвижной системы относительно неподвижной. Пусть положение т. А определено в двух системах отсчета: неподвижной OXYZ и подвижной O'X'Y'Z'
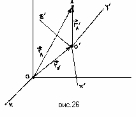
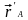
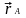
н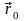 еподвижной
системе положение т. А
определяются радиус-вектором в
подвижной –,
а положение начала подвижной системны
относительно неподвижной определяются
вектором .
еподвижной
системе положение т. А
определяются радиус-вектором в
подвижной –,
а положение начала подвижной системны
относительно неподвижной определяются
вектором .
К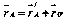 ак
видно из рисунка, связь между
радиус-векторами и ,
определяющими положение точки в обеих
системах отсчета выражается соотношением:
ак
видно из рисунка, связь между
радиус-векторами и ,
определяющими положение точки в обеих
системах отсчета выражается соотношением:
(131)
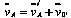 Легко видеть,
что аналогично связаны и векторы скорости
в этих системах (абсолютная и относительная):
Легко видеть,
что аналогично связаны и векторы скорости
в этих системах (абсолютная и относительная):
Но для вектора ускорения при произвольном движении тела и подвижной системы эта связь оказывается более сложной.
Если подвижная система наряду с поступательным совершает и вращательное движение, а тело движется относительно нее, в относительном и переносном ускорениях появляется дополнительный член, одинаковый и для относительного, и для переносного ускорения, обусловленный движением тела во вращающейся системе отсчета. Это происходит даже при равномерном движении тела относительно подвижной системы. Следовательно, с точки зрения наблюдателя подвижного, нарушается основной закон динамики (т.е. подвижная система не попадает в круг систем, определенный первым законом Ньютона).
Системы, в которых выполняется законы Ньютона, называют инерциальными. Инерциальные - это такие системы отсчета, в которых ускорение вызывается только действием сил, а сами силы появляется только в результате взаимодействий тел.
(продолжение 1) 16 .Относительность механического движения. Галилеевы преобразования координат и закон сложения скоростей.
Галилеевы преобразования координат и закон сложения скоростей.
Предположим, что одна из систем отсчета неподвижна, а другая - движется относительно первой с постоянной скоростью, так что оси ОХ,O’Х' и OY ,0'Y' остается параллельными, а ось 0'Y' скользит вдоль OY со скоростью (рис.30).
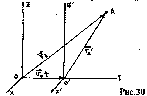
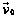
П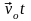 оложение
т. А
можно задать векторным и координатным
способами в обеих системах отсчета.
Будем считать, что в исходный момент
времени системы полностью совпадают.
Тогда к моменту времени t,
измеренному в неподвижной системе,
подвижная система совершит перемещение
. Координаты т. А
в двух системах отсчета связаны
соотношениями:
оложение
т. А
можно задать векторным и координатным
способами в обеих системах отсчета.
Будем считать, что в исходный момент
времени системы полностью совпадают.
Тогда к моменту времени t,
измеренному в неподвижной системе,
подвижная система совершит перемещение
. Координаты т. А
в двух системах отсчета связаны
соотношениями:
х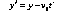 '
= х
(133)
'
= х
(133)
z'=z (135)
Опыт показывает, что течение времени в обеих системах одинаково:
t'=t (136)
Совокупность соотношений (133, 134, 135, 136) и представляет собой преобразования Галилея в координатной форме.
Б
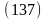 олее
компактную форму принимают преобразования
Галилея, если положение т. А
определять
векторным способом:
олее
компактную форму принимают преобразования
Галилея, если положение т. А
определять
векторным способом:
t' = t (138)
Справедливы и преобразования Галилея для обратного перехода:
х = х' (139)
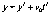 (140)
(140)
z=z' ( 141)
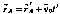 t=t’
(142)
или
t=t’
(142)
или
(143)
t = t' (144)
Скорость т. А в двух системах отсчета связана соотношением: