
- •1.Определение положения точки в пространстве. Вектор перемещения.
- •2. Вектор скорости. Вектор ускорения. Тангенциальное и нормальное ускорение
- •3.Кинематика твердого тела. Число степеней свободы. Поступательное движение твердого тела.
- •Вращательное движение твердого тела.
- •5.Движение отдельных точек вращающегося твердого тела.
- •6.Плоское движение твердого тела
- •7.Сила. Сложение сил и разложение силы на составляющие. Проекции силы на плоскость и ось.
- •8.Статическое и динамическое проявление сил. Законы Ньютона. Принцип независимости действия сил.
- •10.Основной закон динамики
- •12.Основной закон динамики системы материальных точек.
- •13.Уравнения моментов для системы материальных точек относительно произвольного центра, произвольной оси
- •14.Основной закон динамики тела переменной массы (уравнение Мещерского)
- •15.Первое и второе соотношение Циолковского.
- •15.Первое и второе соотношение Циолковского.(продолжение1)
- •16.Относительность механического движения. Галилеевы преобразования координат и закон сложения скоростей.
- •17.Постулаты Эйнштейна. "Радиолокационный" метод (метод коэффициента "k ").
- •17.(Продолжение)Постулаты Эйнштейна. "Радиолокационный" метод (метод коэффициента "k ").
- •18.Замедление" хода времени. Относительная скорость.
- •19.Сравнение поперечных размеров тел. Эффект "сокращения" длин.
- •19.Сравнение поперечных размеров тел. Эффект "сокращения" длин.(продолжение)
- •20. Преобразования Лоренца. Интервал. Инвариантность интервала.
- •Релятивистская масса, релятивистский импульс. Релятивистское уравнение движения.
- •Релятивистская масса, релятивистский импульс.
- •23.Неинерциальные системы отсчёта. Силы инерции. Силы инерции во вращающихся системах отсчета. Силы инерции Кориолиса
- •23.Силы трения. Сухое трение. Силы трения качения
- •23.Силы трения. Сухое трение. Силы трения качения.Силы трения скольжения.(продолжение)
- •24.Вязкое трение. Движение тел в сопротивляющейся среде.
- •25.Упругие силы. Продольное сжатие и растяжение. Закон Гука
- •26.Деформация сдвига и кручения.
- •27.Закон всемирного тяготения.
- •28. Потенциальная энергия гравитационного взаимодействия, гравитационный потенциал. Связь напряжённости и потенциала поля.
- •29.Работа и энергия. Работа силы тяжести. Работа упругих сил
- •30.Работа и кинетическая энергии. Потенциальная энергия. Закон сохранения энергии
- •31. Момент инерции твёрдого тела. Теорема Штейнера. Моменты инерции тел простой формы
- •Вращательное движение
- •34. Гироскопы. Прецессия волчка.
- •Давление покоящейся жидкости
- •Уравнение гидростатики Эйлера.
- •. Уравнение поверхности уровня.
- •Закон Паскаля
- •Сообщающиеся сосуды, заполненные однородной жидкостью.
- •Закон Архимеда.
- •Механика движущихся жидкостей. Расход жидкости. Уравнение неразрывности струи жидкости
- •Определения
- •Уравнение Бернулли. Формула Торричелли.
- •Примеры применения закона бернулли формула торичелли
- •Ламинарное и турбулентное течение жидкости. Число Рейнольдса.
- •43.Колебательное движение. Характеристики колебаний.
- •44.Собственные колебания
- •45. Затухающие колебания.
- •48.Геометрическое представление колебаний
- •49.Сложение одинаково направленных колебаний. Частоты складываемых колебаний одинаковы
- •50.Сложение одинаково направ. Колебаний. Частоты складываемых колебаний различны, одинаковы амплитуды и начальные фазы.
- •51.Сложение взаимно перпендикулярных колебаний.
- •53.Б) Колебания пилообразной формы
- •54.В) Колебания треугольной формы
13.Уравнения моментов для системы материальных точек относительно произвольного центра, произвольной оси
П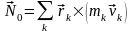 о
определению моментом импульса системы
точек относительно центра называют
векторную сумму моментов импульса всех
точек системы относительно того же
центра:
о
определению моментом импульса системы
точек относительно центра называют
векторную сумму моментов импульса всех
точек системы относительно того же
центра:
Д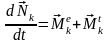 ля
каждой точки системы можно записать
уравнение моментов в виде:
ля
каждой точки системы можно записать
уравнение моментов в виде:

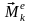
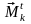
где: ― сумма моментов внешних сил, приложенных к k-й точке, а ― сумма моментов внутренних сил, приложенных к k-й точке.
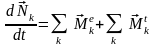
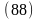 Суммируя уравнения
моментов для всех точек системы, получим:
Суммируя уравнения
моментов для всех точек системы, получим:
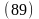 Учитывая, что
векторная сумма моментов всех сил равна
нулю,
Учитывая, что
векторная сумма моментов всех сил равна
нулю,
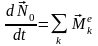 Совершенно
аналогично выводится уравнение моментов
относительно произвольной оси:
Совершенно
аналогично выводится уравнение моментов
относительно произвольной оси:

где: ― сумма моментов внешних сил относительно произвольной оси Z.
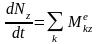

14.Основной закон динамики тела переменной массы (уравнение Мещерского)
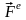 Предположим,
что в момент времени t
основное тело (корпус ракеты) имело
массу М, двигалось со скоростью ,
а равнодействующая внешних приложенных
к нему сил
Предположим,
что в момент времени t
основное тело (корпус ракеты) имело
массу М, двигалось со скоростью ,
а равнодействующая внешних приложенных
к нему сил
р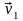 авнялась
. Через малый промежуток времени
dt,
т.е. в момент времени t+dt
от основного тела отделилась масса –dM
(dM<0),
движущаяся со скоростью .
авнялась
. Через малый промежуток времени
dt,
т.е. в момент времени t+dt
от основного тела отделилась масса –dM
(dM<0),
движущаяся со скоростью .
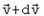 Основное тело в
этот момент имеет массу M+dМ
и движется со скоростью .
Основное тело в
этот момент имеет массу M+dМ
и движется со скоростью .
П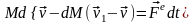 рименим
к системе «основное тело ― отделяющаяся
масса» основной закон динамики для
системы точек:
рименим
к системе «основное тело ― отделяющаяся
масса» основной закон динамики для
системы точек:

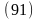
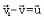
 Пренебрегая
величинами второго порядка малости,
можем записать:
Пренебрегая
величинами второго порядка малости,
можем записать:
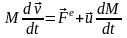 Обозначив
(скорость продуктов сгорания топлива
относительно корпуса ракеты), получим
основной закон динамики для тела с
убывающей массой:
Обозначив
(скорость продуктов сгорания топлива
относительно корпуса ракеты), получим
основной закон динамики для тела с
убывающей массой:
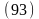

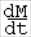 От второго закона
Ньютона выражение (93) отличается величиной
, имеющей размерность силы.
Учитывая, что dM<0,
отметим,
От второго закона
Ньютона выражение (93) отличается величиной
, имеющей размерность силы.
Учитывая, что dM<0,
отметим,
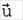 что
при отделении массы от основного тела
на него действует
что
при отделении массы от основного тела
на него действует
дополнительная сила, равная произведению массового расхода на относительную скорость ,
а направлена эта сила противоположно относительной скорости. Такую силу называют реактивной.
15.Первое и второе соотношение Циолковского.
Первое соотношение Циолковского
Первое соотношение Циолковского определяет скорость ракеты в конце активного участка траектории (того участка, на котором работает двигатель). Соотношение получим в предположении, что относительная скорость продуктов сгорания топлива u постоянная (1-я гипотеза Циолковского). Кроме того, будем считать, что ракета движется вне силовых полей.
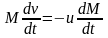
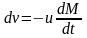

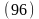
 .Тогда в
проекциях на направление движения
ракеты уравнение Мещерского можно
представить в виде (96 или 97)
.Тогда в
проекциях на направление движения
ракеты уравнение Мещерского можно
представить в виде (96 или 97)
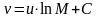
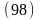 Интегрируя,
получим:
Интегрируя,
получим:

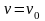
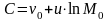
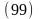 Постоянную
интегрирования С определим из условий
для начала активного участка , когда
,а . Тогда:
Постоянную
интегрирования С определим из условий
для начала активного участка , когда
,а . Тогда:
 Подставив в (98)
найденное значение постоянной
интегрирования, получаем:
Подставив в (98)
найденное значение постоянной
интегрирования, получаем:
 Таким образом, в
любой точке активного участка траектории
можно определить скорость
Таким образом, в
любой точке активного участка траектории
можно определить скорость

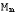
 ракеты
v,
зная её массу в этот момент. Отметим,
что начальная масса ракеты состоит из
массы корпуса и массы топлива
, содержащегося в нём: .
ракеты
v,
зная её массу в этот момент. Отметим,
что начальная масса ракеты состоит из
массы корпуса и массы топлива
, содержащегося в нём: .
В конце активного участка топливо полностью
сгорает, и масса ракеты определяется
только массой её корпуса.
конце активного участка топливо полностью
сгорает, и масса ракеты определяется
только массой её корпуса.
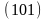 Тогда скорость
ракеты в конце активного участка
траектории равна:
Тогда скорость
ракеты в конце активного участка
траектории равна:
Анализ полученного соотношения позволяет указать пути повышения скорости ракеты.
