
- •1.Определение положения точки в пространстве. Вектор перемещения.
- •2. Вектор скорости. Вектор ускорения. Тангенциальное и нормальное ускорение
- •3.Кинематика твердого тела. Число степеней свободы. Поступательное движение твердого тела.
- •Вращательное движение твердого тела.
- •5.Движение отдельных точек вращающегося твердого тела.
- •6.Плоское движение твердого тела
- •7.Сила. Сложение сил и разложение силы на составляющие. Проекции силы на плоскость и ось.
- •8.Статическое и динамическое проявление сил. Законы Ньютона. Принцип независимости действия сил.
- •10.Основной закон динамики
- •12.Основной закон динамики системы материальных точек.
- •13.Уравнения моментов для системы материальных точек относительно произвольного центра, произвольной оси
- •14.Основной закон динамики тела переменной массы (уравнение Мещерского)
- •15.Первое и второе соотношение Циолковского.
- •15.Первое и второе соотношение Циолковского.(продолжение1)
- •16.Относительность механического движения. Галилеевы преобразования координат и закон сложения скоростей.
- •17.Постулаты Эйнштейна. "Радиолокационный" метод (метод коэффициента "k ").
- •17.(Продолжение)Постулаты Эйнштейна. "Радиолокационный" метод (метод коэффициента "k ").
- •18.Замедление" хода времени. Относительная скорость.
- •19.Сравнение поперечных размеров тел. Эффект "сокращения" длин.
- •19.Сравнение поперечных размеров тел. Эффект "сокращения" длин.(продолжение)
- •20. Преобразования Лоренца. Интервал. Инвариантность интервала.
- •Релятивистская масса, релятивистский импульс. Релятивистское уравнение движения.
- •Релятивистская масса, релятивистский импульс.
- •23.Неинерциальные системы отсчёта. Силы инерции. Силы инерции во вращающихся системах отсчета. Силы инерции Кориолиса
- •23.Силы трения. Сухое трение. Силы трения качения
- •23.Силы трения. Сухое трение. Силы трения качения.Силы трения скольжения.(продолжение)
- •24.Вязкое трение. Движение тел в сопротивляющейся среде.
- •25.Упругие силы. Продольное сжатие и растяжение. Закон Гука
- •26.Деформация сдвига и кручения.
- •27.Закон всемирного тяготения.
- •28. Потенциальная энергия гравитационного взаимодействия, гравитационный потенциал. Связь напряжённости и потенциала поля.
- •29.Работа и энергия. Работа силы тяжести. Работа упругих сил
- •30.Работа и кинетическая энергии. Потенциальная энергия. Закон сохранения энергии
- •31. Момент инерции твёрдого тела. Теорема Штейнера. Моменты инерции тел простой формы
- •Вращательное движение
- •34. Гироскопы. Прецессия волчка.
- •Давление покоящейся жидкости
- •Уравнение гидростатики Эйлера.
- •. Уравнение поверхности уровня.
- •Закон Паскаля
- •Сообщающиеся сосуды, заполненные однородной жидкостью.
- •Закон Архимеда.
- •Механика движущихся жидкостей. Расход жидкости. Уравнение неразрывности струи жидкости
- •Определения
- •Уравнение Бернулли. Формула Торричелли.
- •Примеры применения закона бернулли формула торичелли
- •Ламинарное и турбулентное течение жидкости. Число Рейнольдса.
- •43.Колебательное движение. Характеристики колебаний.
- •44.Собственные колебания
- •45. Затухающие колебания.
- •48.Геометрическое представление колебаний
- •49.Сложение одинаково направленных колебаний. Частоты складываемых колебаний одинаковы
- •50.Сложение одинаково направ. Колебаний. Частоты складываемых колебаний различны, одинаковы амплитуды и начальные фазы.
- •51.Сложение взаимно перпендикулярных колебаний.
- •53.Б) Колебания пилообразной формы
- •54.В) Колебания треугольной формы
Вращательное движение твердого тела.
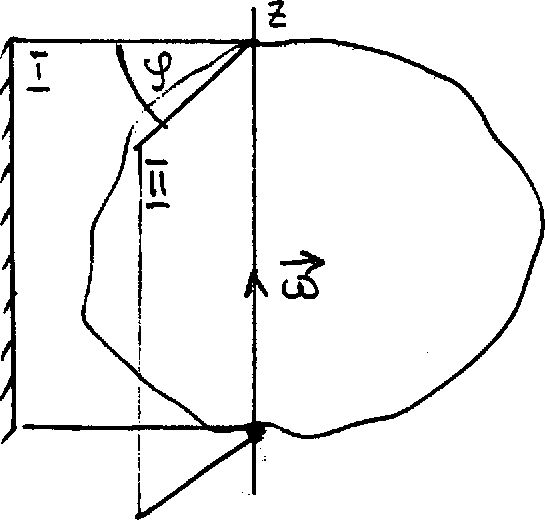 Рис.
10
Рис.
10
Вращательным называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными в пространстве. Прямая, проходящая через неподвижные точки тела, называются осью вращения. При вращательном движении все точки тела движутся в параллельных плоскостях, описывая концентрические окружности, центры которых лежат на оси вращения.
Пусть тело вращается вокруг неподвижной оси Z (рис. 10). Для определения положения этого тела в пространстве через ось вращения проведем две плоскости: 1 - неподвижную и 2 - связанную с телом и вращающуюся вместе с ним. Положение тела задается углом между плоскостями (угловой координатой). Изменение угловой координаты задает угловое перемещение . Кинематический закон движения тела задан, если известна угловая координата в любой момент времени: = (t).
Б ыстрота
вращения определяется угловой скоростью.
ыстрота
вращения определяется угловой скоростью.
С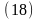
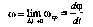
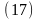 редней
угловой скоростью называют величину:
(17). А мгновенной (18)
редней
угловой скоростью называют величину:
(17). А мгновенной (18)
д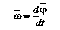
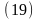 ля
определения
как вектора необходимо угол поворота
(угловое перемещение) также определять
как вектор. Вектором углового
перемещения называют вектор, направленный
вдоль оси вращения в ту сторону, откуда
вращение тела видно происходящим против
хода часовых стрелок. По такому определению
вектор угловой скорости равен:
ля
определения
как вектора необходимо угол поворота
(угловое перемещение) также определять
как вектор. Вектором углового
перемещения называют вектор, направленный
вдоль оси вращения в ту сторону, откуда
вращение тела видно происходящим против
хода часовых стрелок. По такому определению
вектор угловой скорости равен:
В случае вращения тела, показанном на рис. 10, вектор угловой скорости направлен вверх вдоль оси вращения.
В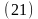
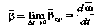
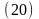
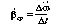 ектором
среднего углового ускорения называют
вектор (20)_а мгновенного(21)
ектором
среднего углового ускорения называют
вектор (20)_а мгновенного(21)
Легко видеть, что при ускоренном вращении твердого тела вектор углового ускорения направлен вдоль оси вращения в ту же сторону, что и вектор угловой скорости, а при замедленном - вдоль оси вращения противоположно вектору угловой скорости.
5.Движение отдельных точек вращающегося твердого тела.
Х

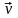 отя
все точки вращающегося тела имеют
одинаковые и кинематические
отя
все точки вращающегося тела имеют
одинаковые и кинематические
х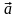 арактеристики
их движения ( и ) различаются.
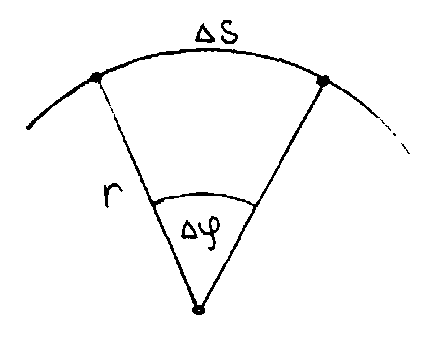
Предположим, что произвольная точка
вращающегося тела находится на расстоянии
г от оси вращения (рис.11).
арактеристики
их движения ( и ) различаются.
Предположим, что произвольная точка
вращающегося тела находится на расстоянии
г от оси вращения (рис.11).
З
 а
промежуток времени t
проходит по своей траектории путь S
. Средняя скорость точки при этом равна:
21 и мгновенная(22)
а
промежуток времени t
проходит по своей траектории путь S
. Средняя скорость точки при этом равна:
21 и мгновенная(22)
С учетом направлений векторов угловой и
линейной скорости, а также радиус-вектора
рассматриваемой точки, получим:
учетом направлений векторов угловой и
линейной скорости, а также радиус-вектора
рассматриваемой точки, получим:

У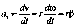
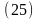

 скорение
отдельных точек вращающегося твердого
тела удобно определять по отдельным
его составляющим
at,
an:
скорение
отдельных точек вращающегося твердого
тела удобно определять по отдельным
его составляющим
at,
an:
П
 олное
ускорение точки равно
олное
ускорение точки равно
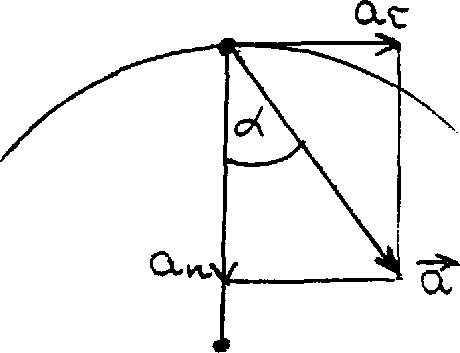 рис 12
рис 12
К
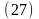 ак
видно из приведенных соотношений, полное
ускорение и отдельные его составляющие
зависят от расстояния r до оси вращения.
Направление вектора ускорения при таком
представлении определяется углом
отклонения
вектора ускорения от радиуса вращения
(рис. 12).
ак
видно из приведенных соотношений, полное
ускорение и отдельные его составляющие
зависят от расстояния r до оси вращения.
Направление вектора ускорения при таком
представлении определяется углом
отклонения
вектора ускорения от радиуса вращения
(рис. 12).
Из рис. 12 видно, что
Таким образом, угол отклонения вектора полного ускорения от радиуса вращения одинаков для всех точек тела.
