Примеры применения закона бернулли формула торичелли

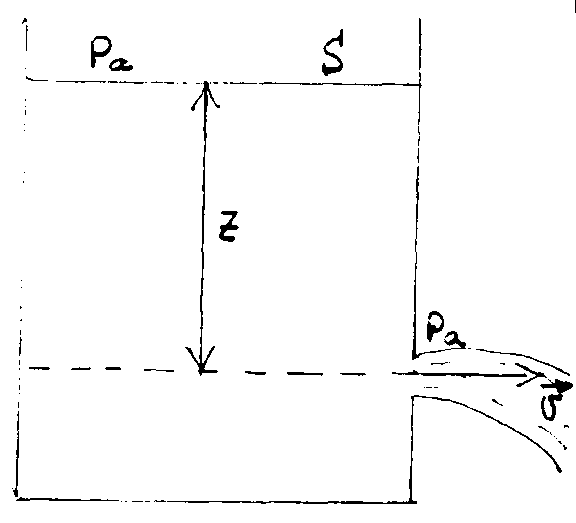
(рис. 76)

формула Торричелли позволяет определить скорость истечения жидкости из отверстия в сосуде. Предположим, что в широкий сосуд площади сечения S налита жидкость, свободная поверхность которой находится на высоте Z над центром малого отверстия площади в боковой стенке сосуда (рис.76). Давление на свободной поверхности жидкости н в вытекающей струе непосредственно за отверстием равно атмосферному Р_а. Пусть скорость истечения жидкости равна , а скорость понижения уровня жидкости в сосуде - . Жидкость будем считать несжимаемой.

Запишем уравнение Бернулли, сравнивая сечение для свободной поверхности жидкости с сечением отверстия:

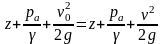
Т.к. площадь сечения отверстия мала по сравнению с сечением сосуда, а жидкость несжимаема, то:

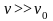
откуда следует формула Торричелли:

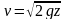
37. Ламинарное и турбулентное течение жидкости. Число Рейнольдса.

Ламинарным называют упорядоченное, слоистое течение жидкости. Моделью такого течения является относительное движение звеньев телескопической антенны. Ламинарное течение возможно в жидкостях при относительно малых скоростях потока, если же скорость потока увеличивать, то в нем возникают вихри. Когда вихри занимают весь объем потока, последний называется вихревым или турбулентным. Образование вихрей связано с взаимодействием частиц слоев жидкости и переносом импульса из слоя в слой. Переносу содействуют силы инерции, а препятствуют - силы вязкого тре­ния. Поэтому критерием перехода от ламинарного течения к турбу­лентному может служить отношение этих сил. В общем случае, не­зависимо от формы потока, следует рассматривать некоторые харак­теристические параметры потока, например, характеристические размеры и т.д. Силу вязкого трения можно выражать из закона Ньютона для вязкого трения, а силу инерции - по определению:

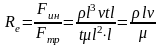(301)

П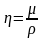 олученное выражение называется числом (критерием) Рейнольдса. Вводя понятие кинематической вязкости, число Рейнольдса можно записать и так: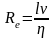

где - кинематическая вязкость жидкости.

Формула Пуайзеля

(рис. 80)

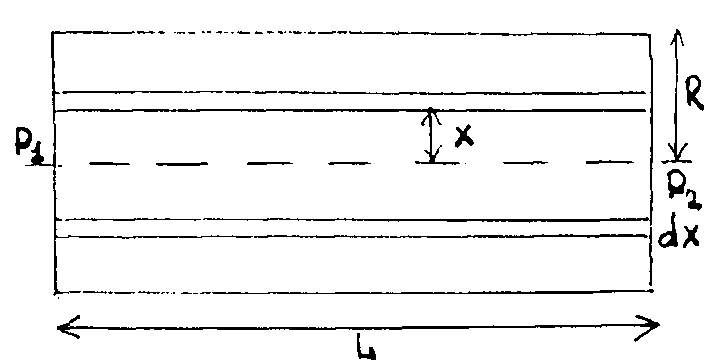
Формула Пуазейля дает величину объемного расхода жидкости при ламинарном течении жидкости по цилиндрическим трубам. Рассмотрим установившийся поток жидкости по цилиндрической трубе радиуса R и длины L , ось которой горизонтальна (рис.80). давление в левом сечении трубы равно P₁ , а в правом Р₂ , причем P₁>P₂ . Скорость потока максимальна вдоль оси трубы и равна ну ли у стенок, выделим в трубе тонкий цилиндрический слой радиуса х и толщины dx , в пределах которого скорость жидкости можно считать одинаковой. На торцы выделенного слоя действует силы давления, равнодействующая которых равна: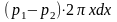

На внутреннюю и внешнюю поверхности слоя действуют силы вязкого трения. По закону Ньютона для вязкого трения на внутреннюю поверхность слоя действует сила:

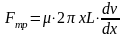
(продолжение) 43. Ламинарное и турбулентное теч-е жидк- ти. Число Рейнольдса.

а равнодействующая сил вязкого трения, приложенных к внутренней и внешней поверхностям, соответственно равна:

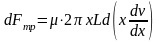
Так как жидкость движется с постоянной скоростью, сумма приложенных к слою сил равна нулю, т.е.:

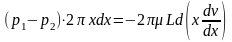. Интегрируя , получим: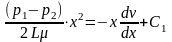

Постоянную интегрирования С₁ можно получить из условия, что вдоль оси трубы скорость максимальна:

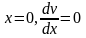
следовательно С₁=0. С учетом этого:

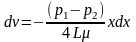(304)

Интегрируя (304), получим:

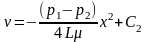Постоянную интегрирования С₂ получим из условия, что у стенок трубы скорость жидкости равна нулю x=R, , V=0, поэтому:

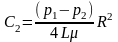
Подставив найденное значение постоянной интегрирования в общее решение, получим зависимость скорости жидкости от расстояния до оси трубы:

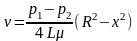(305)

Для определения объемного расхода запишем сначала элементарный объемный расход по выделенному цилиндрическому слою:

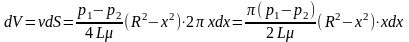(306)

Полный объемный расход по всей трубе получим интегрированием (306) по всем слоям:

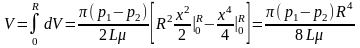(307)

Выражение (287) называет формулой Пуазейля.