34. Давление покоящейся жидкости

(рис.68 )

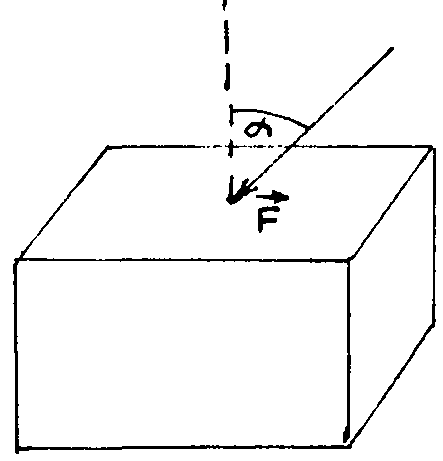
Выделим в объеме покоящейся жидкости небольшой объем (рис. 68), пусть на грань этого объема действует со стороны окружающих слоев сила давления F.

Из опыта известно, что трение покоя в жидкостях отсутствует, т.е. должны от­сутствовать касательные усилия к выделенной грани.

Средним давлением называют величину: , где dF сила давления, действующая на площадку площади dS.

Истинным давлением или давлением в точке называют величину:

(276)

В покоящейся жидкости давление в точке не зависит от ориентировки площадки, на ко­торую оно действует, действительно, в покоящейся: жидкости выделим небольшой объем, фор­ма которого показана на рис. 69. На каждую грань объема действует силы давления, поскольку объем покоится, в каждом из координатных направлений сумма сил равна нулю:

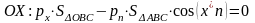
т. к.

т.е.

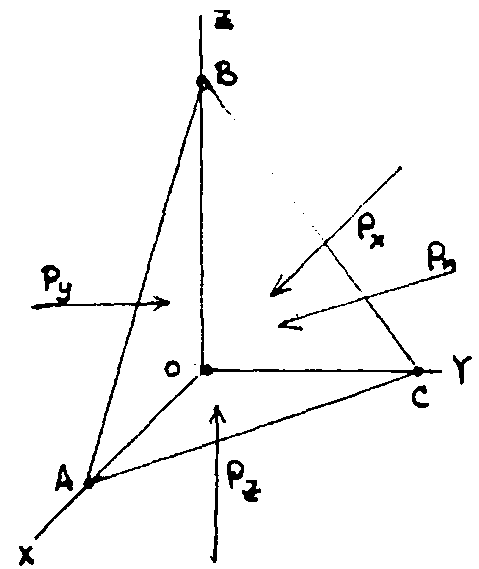(рис. 69)

Аналогично можно показать, что: . Следовательно:

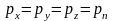
34. Уравнение гидростатики Эйлера.

.

Впокоящейся жидкости выделим малый ее объем dV=dxdydz в фор­ме прямоугольного параллелепипеда (рис. 70).

Известно давление в центре объема p и изменение давления на единицу длины в каждом из координат­ных направлений:

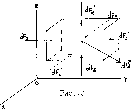
На каждую грань объема действуют силы давления, а на весь объем - объемные (массовые) силы, например, сила тяжести. Поскольку объем покоится, сумма проекции всех сил по каждому из координатных направлений равна нулю.

На заднюю грань действует сила давления:

а на переднюю:

Кроме того, в этом направлении действует составляющая мас­совой силы d, которую можно определить по второму закону Ньютона:

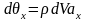
где:  - плотность среды, a_x- ускорение, которое способна сообщить массовая сила. Т. к. объем покоится,

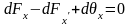
т.е.

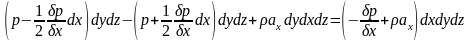
Поскольку : (277)

Аналогично для других координатных направлений: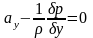 (278)

(279)

(277), (278), (279) и представляют собой систему уравне­ний гидростатики Эйлера

36. . Уравнение поверхности уровня.

.

Поверхностью уровня называют такую поверхность, во всех точках которой давление одинаково (dP=0)

то, с учетом уравнение Эйлера:

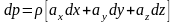
для поверхности уровня:

(280)

В случае идеальной жидкости:

(281)

Пример, Пусть жидкость покоится в поле тяготения 3емли.

Плоскость 0XY горизонтальна, а ось z направлена вертикально вверх. В этом случае:

Тогда:

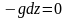
т.е. z=const, т.о. поверхности уровня (в частности, свободная поверхность) горизонтальны.

37. Закон Паскаля

Жидкость покоится в поле тяготения Земли. В этом случае уравнения Эйлера имеют вид:

(282)

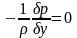(283)

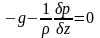( 284)

С учетом (282) и (283) последнее уравнение (284) принимает вид:

(285)

откуда:

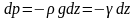(286)

где 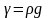удельный вес жидкости. Интегрируя (286), получаем

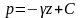(287)

Постоянная интегрирования будет определена, если в точке с координатой z₀ известно давление p₀ . Тогда

Последнее выражение обычно записывают в виде:

(288)

т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.