1. Вращательное движение

СВОБОДНЫЕ ОСИ ВРАЩЕНИЯ

Момент импульса тела в произвольном случае его вращения не совпадает по направлению с вектором угловой скорости вращения. Тем не менее, существует такие оси, при вращении вокруг которых момент импульса и угловая скорость по направлению сов­падают. Такие оси называются главными осями инерции (свободными осями вращения). Таких осей в каждом теле три, все они взаимноперпендикулярны и проходят через центр масс тела, поэтому их удобно принимать в качестве системы отсчета для каждой из этих осей , , .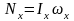

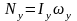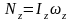В случае произвольного по форме тела легко показать, что 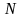и (омега) не совпадает по направлению (рис. 62).

Кинетическая энергия тела при таком вращении может быть представлена суммой энергий вращения вокруг трех главных осей:

или: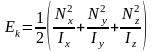

или:

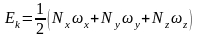
или:

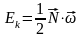
Напр-е векторов и можно указать заданием направляющих косинусов, например: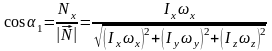

(продолжение) 32. Кинетическая энергия твёрдого тела для различных типов движения.

очевидно, что направления и совпадают в том слу­чае, если: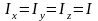 (267)

Твердое тело, отвечающее условию (267), называется шаровым волчком. Твердое тело, у которого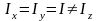 , называется симметричным волчком с осью симметрии .

Твердое тело, у которого все три главных момента инерции различны, называет несимметричным волчком .

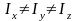СВОБОДНОЕ ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА

Свободным называют такое вращение тела, при котором сумма моментов внешних сил, приложенных к телу, равна нулю:

Отсюда следует, что при свободном вращениии .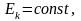

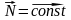
Рассмотрим свободное вращение симметричного волчка с осью симметрии .Кинетическая энергия для него равна:

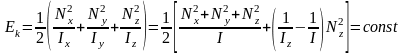
В этом выражении первое слагаемое постоянно, следовательно, постоянно и второе, т.е.:

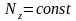(268)

Учитывая, что получаем: (269)

Написав выражение для кинетической энергии в виде:

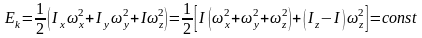
делаем вывод, что: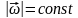 (270)

наконец, кинетическую энергию представим в виде:

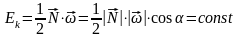(271)

где  - угол между векторами и .Из (271) следует, что,

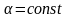(272)

Учитывая (269), (270), (271) ,(272) свободное вращение тела можем представить как вращение оси симметрии тела вокруг неподвижного направления . При этом относительное расположение 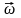, 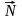и 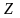со временем сохраняется (рис.53). Такое вращение при отсутствии моментов внешних сил называется регулярной прецессией. Тело вращается вокруг оси симметрии со скоростью 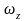, a сама ось описывает коническую поверхность, вращаясь вокруг неподвижного направления с угловой скоростью прецессии .

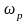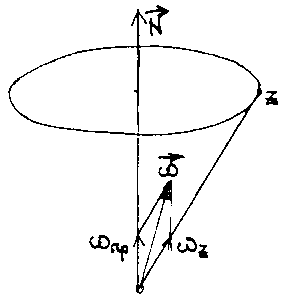Т. o . для вращающегося тела можно выделить три оси - момента импульса., угловой скорости и оси симметрии.

34. Гироскопы. Прецессия волчка.

Гироскопы.

Рассмотрим быстро вращающийся относительно оси симметрии массивный диск (рис.64). При очень быстром вращении диска, как было сказано выше, векторы момента импульса и угловой скорости направлены вдоль оси симметрии.

Если к концам оси вращения приложить пару сил, ее момент будет изменять момент импульса в соответствии с уравнением моментов: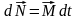

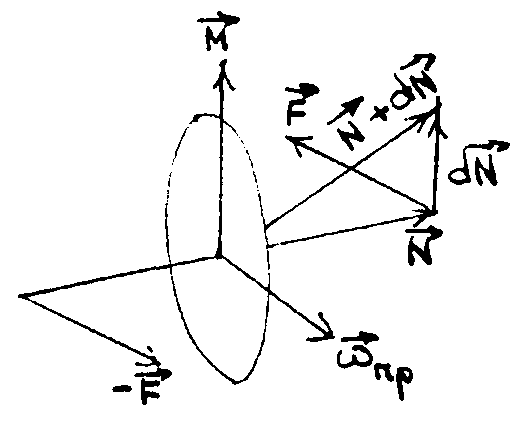
рис. 64)

Через промежуток времени момент импульса изменит свое направление и станет равным Соответственно изменится и положение оси симметрии. Как видно, силы пары приложены в горизонтальной плоскости, а ось вращается под действием момента - в вертикальной.

Уравнение моментов в скалярном виде в этом случае представляют следующим образом:

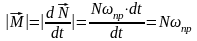
С учетом направлений векторов уравнение моментов для быстро вращающегося тела записывает в векторной форме так: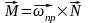 (273)

Гироскопом называют массивное тело, очень быстро вращающееся вокруг оси симметрии. Наиболее часто применяются гироскопы в кардановых подвесах. В таких подвесах при любом повороте оси вращения центр масс гироскопа остается неподвижным (рис.65) Нa рисунке представлен карданов подвес для гироскопа с двумя степенями свободы.

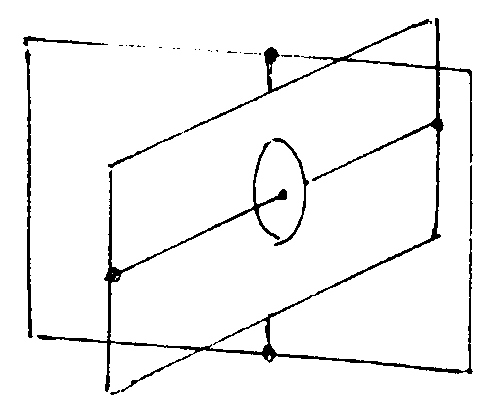
Рис.65

(продолжение)34. Гироскопы. Прецессия волчка.

Для определения угловой скорости прецессии удобно пользоваться следующими соображениями. Масштаб измерения можно выбрать таким, что конец вектора совпадает с концом оси гироскопа (рис. 66).

(рис. 66)

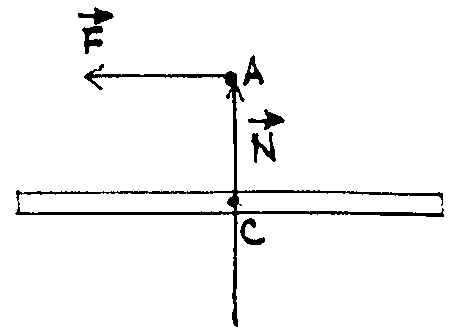
При действии на конец оси (в т. А) силы ее момент вызовет прецессион­ное вращение. По уравнению моментов

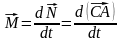
Но можно рассматривать как радиус-вектор т. A относительно центра масс. Тогда, по определению:

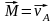(274)

Прецессия волчка.

Быстро вращающийся симметричный волчок установлен на горизонтальную поверхность (рис. 67). Точка касания неподвижна. Прецессия волчка вызывается моментом силы тяжести так как линия действия реакции проходит через неподвижный центр .

при указанном направлении вращения момент силы тяжести вызывает пре­цессию в направлении, указанном на рисунке. Угловую скорость прецессии

(рис. 67)

можно определить, пользуясь (274):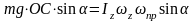

т.е.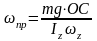 (275)

Следовательно, угловая скорость прецессии тем меньше, чем больше угловая скорость собственного вращения.