1.Определение положения точки в пространстве. Вектор перемещения.

Определение положения точки в пространстве.

Для описания движения точки, т.е. изменения ее положения с течением времени, прежде всего, надо в любой момент времени ука­зать ее местоположение координатным или векторным способом. Оба способа задания положения тела в пространстве эквивалентны, т.е. зная координаты точки, можно указать ее радиус-вектор, и наоборот. Из рис. 1 видно, что радиус-вектор представить можно д иагональю прямоугольного параллелепипеда со сторонами, численно равными координатам точки Х_а, Y_a и Z_a. Отсюда очевидна связь модуля радиус-вектора точки с ее координатами:

Для определения направления радиус-вектора в пространстве можно определить углы , , , которые радиус-вектор образует с координатными осями OX, OY, и OZ соответственно. Тогда:

Таким образом, зная координаты точки, можно определить величину (1) радиус-вектора, и его направление в пространстве по так называемым направляющим косинусам (2), (3) и (4).

При движении точки ее координаты и радиус-вектор с течением времени изменяются, для определения характеристик движения вводят три вектора: перемещения, скорости и ускорения.

Вектор перемещения.

Для определения перемещения точки в пространстве вводят вектор перемещения.

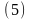
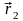
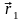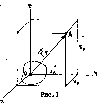
Н апример, за промежуток времени t точка перемещается из положения 1 в положение 2 (рис. 2), определяемые векторным способом указанием радиус-векторов и ; вектором перемещения называют вектор, проведенный из начального положения 1 в конечное 2 перемещаемого тела. Из векторного треугольника видно, что вектор перемещения равен приращению радиус-вектора точки. Наряду с изменением радиус-вектора точки происходит изменение ее координат, т.е. перемещение точки вдоль отдельных координатных направлений. 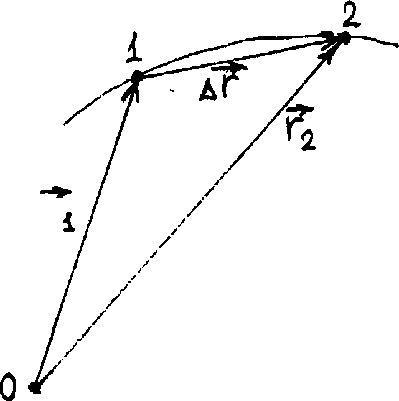Из рис.3 видно, что

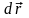
В ектор перемещения за конечный промежуток времени в общем случае не совпадает с направлением движения (направлением касательной к траектории движения). Очевидно, что эти направления будут совпадать в общем случае движения только для бесконечно малых перемещений точки .

2. Вектор скорости. Вектор ускорения. Тангенциальное и нормальное ускорение

Вектор скорости.

Вектором скорости называют вектор, определяющий быстроту и направление движения.

В ектором средней скорости называют отношение вектора перемещения к промежутку времени, за который это перемещение происходит:

Так как в произвольном случае движения вектор перемещения за конечный промежуток времени не определяет точно направление движения, это не может сделать и вектор средней скорости. Следо­вательно, необходимо рассматривать перемещения за бесконечно ма­лые промежутки времени.

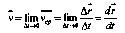
Вектором истинной (мгновенной) скорости называют предел, к которому стремится значение вектора средней скорости при бесконечном убывании промежутка времени:

Так как при движении тела в общем случае изменяются все три его координаты, часто бывает удобным рассматривать скорость дви­жения точки вдоль отдельных координатных направлений (компоненты или составляющие вектора скорости). Компоненты средней скорости равны:

К омпоненты же мгновенной скорости определяются как

Вектор скорости с его компонентами связан такими же по виду соотношениями, как радиус-вектор с

к оординатами точек:

В ектор ускорения.

Вектором ускорения называют вектор, определяющий быстроту и направление изменения вектора скорости. Аналогично определени­ям для вектора скорости вводятся понятия среднего и мгновенного

у скорения:

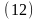
При движении точки по произвольной траектории вектор изме­нения скорости Δ и, следовательно, вектор ускорения направлены в сторону вогнутости траектории независимо от того, увеличивается или уменьшается величина скорости (рис. 4, 5):

Рис. 4. Ускоренное движение Рис. 5. Замедленное движение

Как видно из рисунков, в обоих случаях вектор d направлен в сторону вогнутости траектории. При ускоренном движении он отклоняется в сторону движения, при замедленном - в противоположную

(продолжение) 2.Вектор скорости. Вектор ускорения. Тангенциальное и нормальное ускорение

Для определения мгновенного ускорения надо рассматривать бесконечно малые перемещения, т.е. векторы скорости ₁ и ₂ в соседних точках траектории. Поэтому вектор ускорения лежит в плоскости, содержащей касательную к траектории в данной точке и прямую, параллельную касательной в соседней точке траектории. Такая плоскость называется соприкасающейся. Поэтому наряду с представлением вектора ускорения компонентами

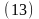
можно рассматривать составляющие вектора в соприкасающейся плос­кости (т.е. только две компоненты). Для определения этих составляющих в любой точке траектории проводят соприкасавшуюся плоскость и в ней две оси - нормальную O_n. в сторону вогнутости траектории и касательную O_t по касательной к траектории. Изменение скорости и, соответственно, ускорение можно рассматривать в проекциях на эти оси (рис. 6).

Двигаясь вдоль траектории, за промежуток времени t точка проходит путь S скорость ее изменяется от  до ₁, при этом ₁ составляет угол  (альфа) с осью O_t. По определению мгновенного ускорения:

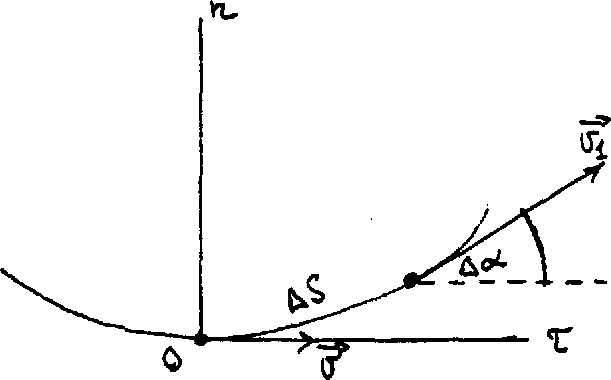
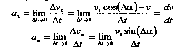рис.6

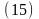
П реобразуем выражение предела, умножив и разделив его на  и S:

О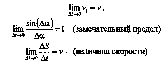 тметим, что при t=0 бесконечно убывает и пройденный путь, и угол (S=0, a=0). При этом условии значения пределов равны:

Предел же называется кривизной траектории К. Кривизна траектории обратно

п ропорциональна радиусу кривизны траектории:

(продолжение2) 2.Вектор скорости. Вектор ускорения. Тангенциальное и нормальное ускорение

С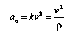 учетом этих замечаний выражение для нормальной составляющей вектора ускорения принимает вид

Для выяснения физического смысла ускорения рассмотрим два частных случая движения.

Р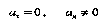 авномерное криволинейное движение (V=const, k<>0). В этом случае, как видно из (14) и

(16),

Н еравномерное прямолинейное движение (V<>соnst , K=0). При таком движении

Следовательно, касательная составляющая ускорения определяет изменение вектора скорости по величине, а нормальная - по направлению.