Электродинамика (конденсированных? сплошных?) сред

Лекция 12. (03.12.2010)

12.1. Пример нелинейного взаимодействия – генерация второй гармоники.

Вместо волнового уравнения – укороченное уравнение для медленно меняющейся амплитуды и фазы

. (16*)

Для поляризации надо определить выражение, которое описывает тот или иной желаемый процесс. Например, если рассматривать генерацию второй гармоники (ГВГ), то наряду с основной волной – волной накачки на заданной частоте будет образовываться и распространяется по среде волна с удвоенной частотой - волна второй гармоники с частотой (несущей волны, если речь о квазигармонических полях) . Напряженность электрического поля этих волн представить можно как

для волны накачки, и

.

для волны гармоники. Нельзя думать, что обязательно , потому что?

Нелинейная поляризация (в главном порядке) может быть записана как

Надо обратить внимание как выписываются аргументы нелинейной восприимчивости и соответственно тому расставляются поля.

С другой стороны,

,

Сравнивая эти выражения, можно заключить, что

, (1.1)

. (1.2)

Эти поляризации (медленно меняющиеся комплексные амплитуды поляризаций) будут медленно меняться в масштабах длин волн и периодов временных осцилляций, если выполняется условие , или . Физически это означает, что волны распространяются с близкими фазовыми скоростями, так что разность фаз, определяющая взаимодействие, накапливается медленно. Условие называется условием (фазового, волнового) синхронизма, а есть мера нарушения синхронизма.

Таким образом. Укороченные уравнения, описывающие ГВГ (и обратный процесс) имеют следующий вид

, (2.1)

, (2.2)

Здесь помечены индексами групповые скорости и направления распространения волн в дифференциальных операторах в левых частях системы уравнения (2). В общем случае они могут различаться.

Аналогично может быть записана система уравнений, описывающая генерацию третье гармоники

, (3.1)

, (3.2)

где теперь и нелинейная восприимчивость третьего порядка. Но, в этих уравнениях не были выписаны слагаемые, отвечающие автомодуляции и кроссмодуляции, которые описываются тоже восприимчивостями третьего порядка.

Если волны накачки и гармоники распространяются в одном (общим для них) направлении, говорят о коллинеарном взаимодействии и коллинеарном синхронизме. В этом случае, условие синхронизма записывается как

.

Что означает

, (4)

или

.

12.2. Коллинеарная генерация второй гармоники вне синхронизма.

Для простоты будет рассматриваться непрерывное излучение, когда от времени медленно меняющиеся амплитуды не зависят. Систему уравнений (2) в этом случае можно переписать как¹

, . (5)

Здесь введены константы

, .

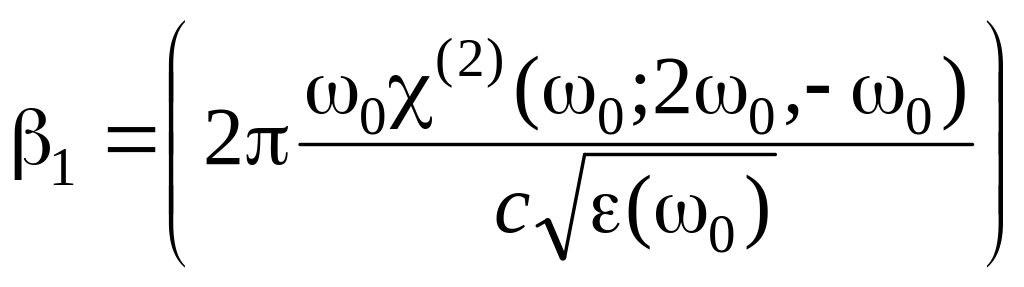В прозрачных средах выполняется некоторое правило, согласно которому

.

Если , то в правой части уравнений (5) быстроменяющийся коэффициент стоит. В этом случае, можно рассмотреть случай, когда амплитуда накачки неизменная, и уравнение для гармоники принимает вид

. (6)

Такое приближение называется приближением заданного поля. Решение этого уравнения, при условии, что гармоника при отсутствует, имеет следующий вид

=

.

Отсюда, «интенсивность»

. (7)

Картинку нарисовать надо. Зависимость интенсивности от длины кристалла и от интенсивности накачки на входе в кристалл.

Длина когерентности – это расстояние, на котором фаза меняется на пи.

.

При этом амплитуда гармоники изменяется от нуля до максимального значения, или, напротив, от максимального значения до нуля.

Если кристалл тонкий, такой что его длина много меньше длины когерентности, то интенсивность гармоники меняется как

. (8)

Но если выполняется условие синхронизма, то это же выражение получается из (7) в пределе . Следовательно, для тонких кристаллов, для которых , условие синхронизма роли не играет.

12.3. Условие синхронизма при ГВГ

Какими способами можно достичь выполнения условия синхронизма, то есть (4)

.

1. В газообразных средах, добавки буферных газов чтобы сдвигать области нормальной и аномальной дисперсии. Можно попытаться получить такую смесь газов, в которой частота накачки лежит в области нормальной дисперсии, а частота гармоники – в области аномальной дисперсии. Условие равенства фазовых скоростей тогда может быть выполнено.

2. В волноводах. Дисперсия зависит от геометрических характеристик волноводов.

3. В анизотропных кристаллах.

4. Неколлинеарный процесс ГВГ.

В случае неколлинеарной ГВГ волны накачки распространяются под некоторым углом друг к другу. Система уравнений тогда должна имеет вид

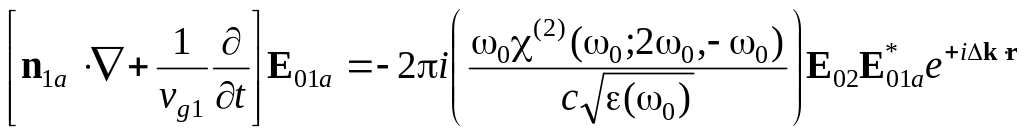, (9.1)

(9.2)

, (9.3)

где . Если выбрать ось Z вдоль направления распространения волны гармоники, ось X – перпендикулярно этому направлению, условие выражается в проекциях волновых векторов как

,

.

Первое из этих условий выполняется всегда. Второе можно переписать как

,

где – угол, под которым пересекаются волны накачки. Выбирая значение этого угла, можно обеспечить выполнение равенства . Это, однако возможно только в случае, если .

В анизотропных кристалла для обыкновенных волн, распространяющихся в произвольном направлении диэлектрическая проницаемость есть . Ксли частоты накачки и гармоники лежат в области нормальной дисперсии, то справедливо неравенство:

.

Для необыкновенных волн диэлектрическая проницаемость зависит от направления распространения волны в кристалле, по отношению к оптической оси. Это направление можно задать углом , таким что .(Лекция 9)

.

Нарисовать картинки.

Если рассмотреть для определенности положительный одноосный кристалл, где для любой частоты, поверхность постоянной фазовой скорости волны на частоте гармоники пересечет поверхность той же фазовой скорости волны накачки.

. (10)

Все направления этого сорта образуют конус, соответствующий угол называется углом синхронизма. Волны накачки и гармоники в направлении распространения, заданном углом будут иметь одинаковые фазовые скорости.