1.2. Основные понятия и характеристики надежности

1.2.1. Понятие случайных событий и случайных величин

Случайное событие – событие, которое может появиться или не появиться в результате данного опыта.

Вероятность случайного события (количественная характеристика случайного события) – теоретическая частота событий, около которой имеет тенденцию стабилизироваться действительная частота события при повторении опыта в данных условиях.

Частота случайного события (статистическая вероятность события) – отношение числа появления данного события к числу всех произведенных опытов.

Случайная величина – величина, которая в результате опыта может принимать то или другое значение (заранее не известно, какое именно). Она может быть либо дискретной, либо непрерывной.

Исчерпывающее представление о случайной величине дает закон распределения случайной величины – соотношение между значениями случайной величины и их вероятностями.

Существуют законы распределения:

1) Интегральный (функция распределения) – вероятность того, что случайная величина X может принимать значения меньше x.

2) Дифференциальный (плотность распределения вероятности случайной величины).

Величины, определяющие характер распределения случайной величины, называются параметрами законов распределения.

Математическое ожидание (среднее значение случайной величины):

Статистическое определение:

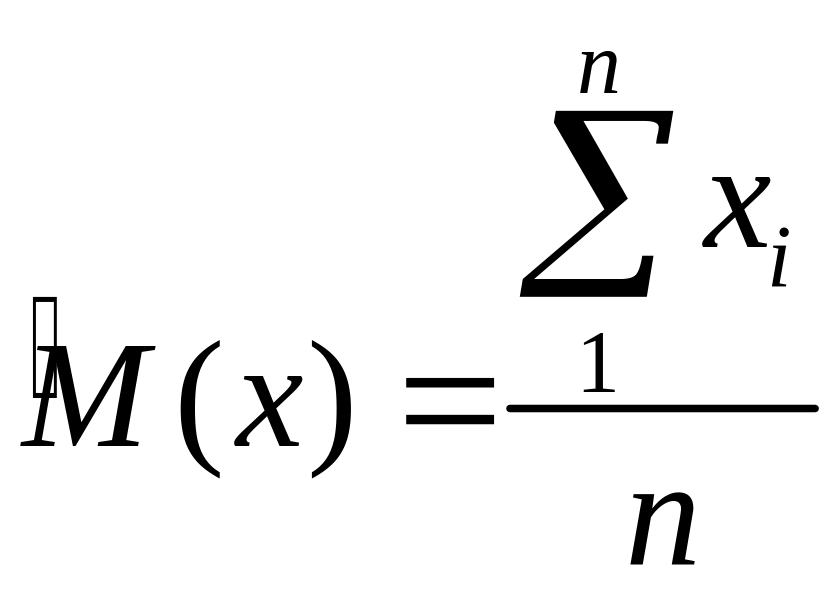
Дисперсия:

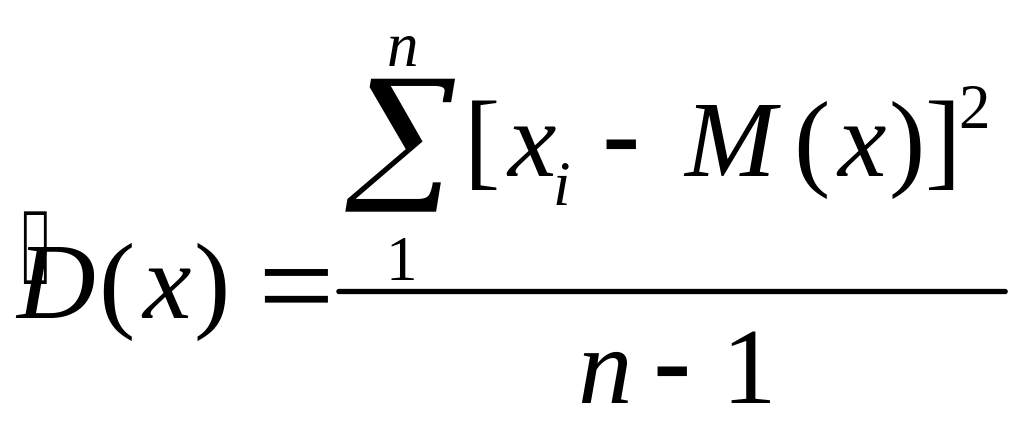
Дисперсия среднего значения:

1.2.2. Невосстанавливаемые элементы и системы

Технические системы, их подсистемы и элементы систем могут работать в режиме, когда восстановление со стороны ремонтного персонала возможно, и в режиме, когда это невозможно либо нецелесообразно. Поэтому для восстанавливаемых и для невосстанавливаемых элементов и систем применяются различные показатели надежности и различные методы расчета надежности.

Показатели надежности невосстанавливаемых объектов:

1) Вероятность безотказной работы объекта P(t) выражает вероятность того, что невосстанавливаемый объект не откажет к моменту времени t.

Если F(t) – функция наработки на отказ, то P(t)=1-F(t).

P(t) обладает следующими свойствами:

а) P(0)=1 (предполагается, что до начала работы изделие является безусловно работоспособным);

б) (предполагается, что объект не может сохранить свою работоспособность неограниченно долго);

в) Если t₂ > t₁, то P(t₂) ≤ P(t₁) (вероятность безотказной работы – функция невозрастающая).

Статистически определить по результатам испытаний можно с помощью следующей формулы:

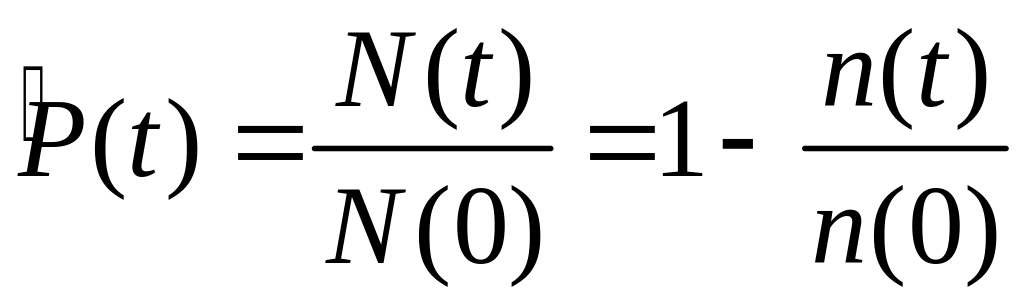
где N(t) – число исправных объектов в момент времени t, n(t) – число отказавших объектов к моменту времени t.

2) Вероятность безотказной работы объекта в интервале времени от t₁ до t₂:

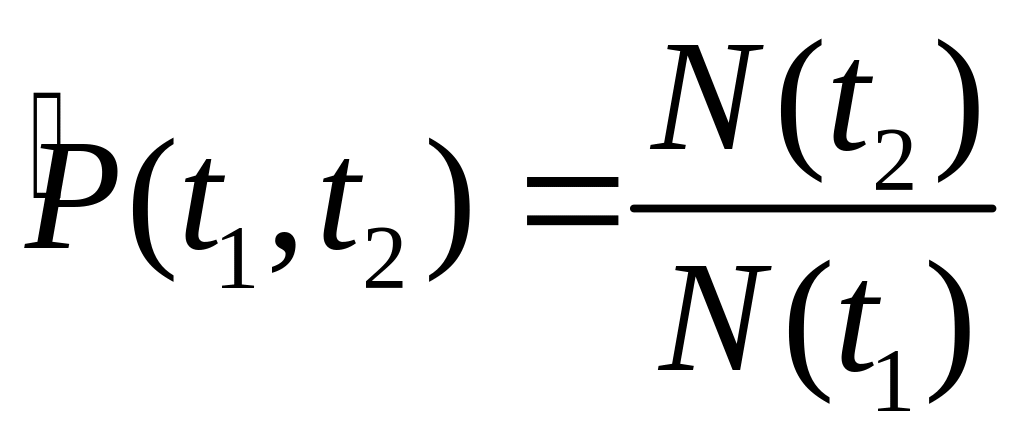
3) Вероятность отказа Q(t) выражает вероятность того, что невосстанавливаемый объект откажет к моменту времени t:

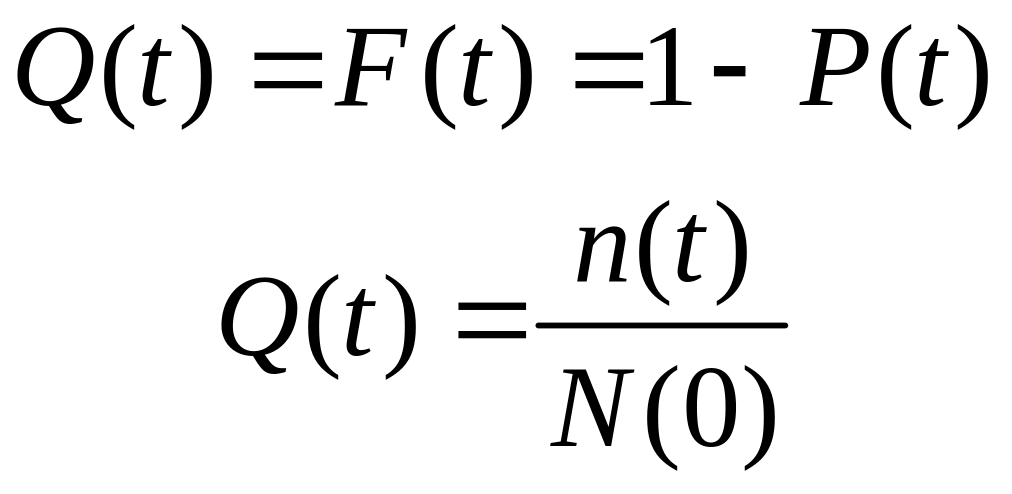
4) Вероятность отказа в интервале времени от t₁ до t₂:

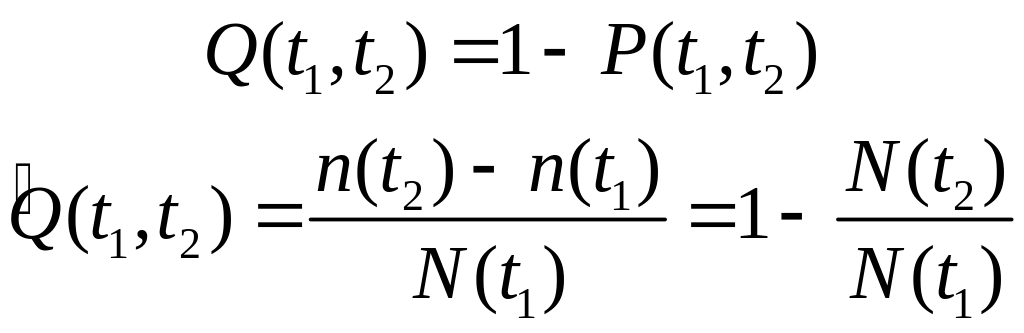
5) Плотность распределения отказов f(t) определяет вероятность возникновения отказа в момент времени t:

Статистическая оценка производится за интервал времени Δt, так как функция f(t) является дифференциальной:

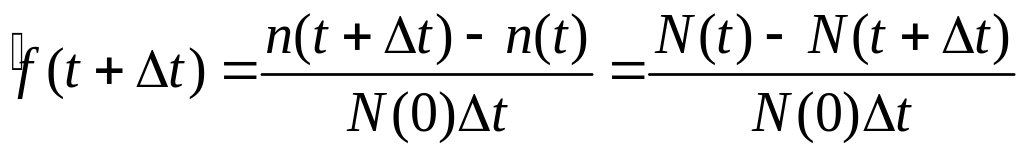
можно рассматривать как среднее число отказов в единицу времени непосредственно после момента t, приходящееся на один элемент из всех объектов, поставленных на испытания.

В связи с этим f(t) на практике обычно называют частотой отказов.

6) Интенсивность отказов λ(t) определяет вероятность возникновения отказа в момент времени t с учетом числа объектов, работоспособных к моменту времени t:

можно рассматривать как среднее число отказов в единицу времени непосредственно после момента t, приходящееся на один элемент, из всех объектов, продолжающих работать к этому моменту t. Отсюда видно, что λ(t) характеризует надежность объекта в момент t более полно, чем f(t), этим и объясняется более широкое применение на практике этого показателя.

Если известна плотность вероятности отказов, то нетрудно определить вероятность отказов или вероятность безотказной работы:

Если известна λ(τ), то

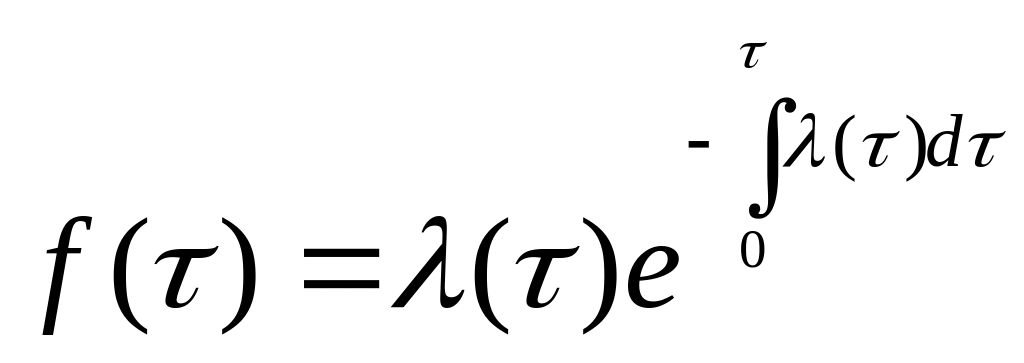
7) Среднее время наработки на отказ T определяется как математическое ожидание времени до отказа:

8) Дисперсия наработки до отказа Dt. Средняя наработка до отказа является точечной оценкой и не говорит ничего о характере распределения времени до отказа. Две совершенно различные функции P₁(t) и P₂(t) (рис. 1) могут характеризоваться одинаковыми значениями средней наработки на отказ

Рис. 1. Пример различной дисперсии

T₁=T₂. Чтобы различать такие случаи наряду с показателем T, используется показатель Dt – дисперсия наработки до отказа или его корень квадратный σ_t – среднеквадратическое отклонение наработки до отказа:

Дисперсия характеризует величину разброса наработки относительно среднего значения:

Где T_i – время до отказа i-го объекта.