3.5. Условия возникновения газообразных включений на стадии пленкообразования

Так как часто реакция пленкообразования является реакцией поликонденсации, то наряду с образованием поперечных связей происходит выделение низкомолекулярных побочных продуктов, которые должны полностью удаляться из лаковой пленки, иначе образуются газообразные включения.

Для описания этого процесса справедливо уравнение диффузии:

, (3.23)

где D – коэффициент диффузии побочных продуктов в окружающую среду;

W – концентрация побочных продуктов в лаковой пленке;

I – количество побочных продуктов, которые выделяются в единицу времени в единице объема.

Левая часть уравнения – количество продуктов, выделившихся в единицу времени. Количество побочных продуктов, которое выделяется при прохождении реакции, пропорционально числу образовавшихся химических связей N₁ = N₀ – N.

,

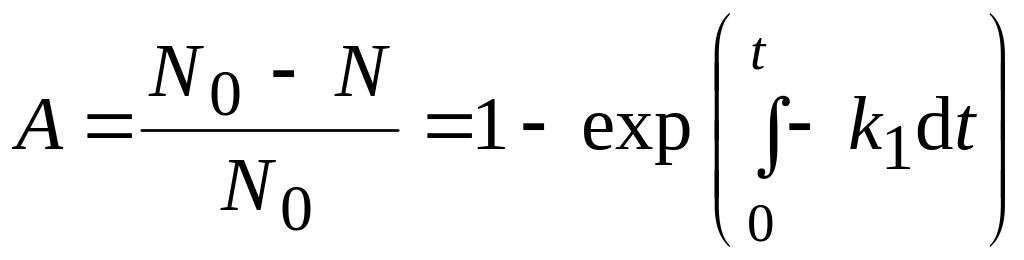откуда

;

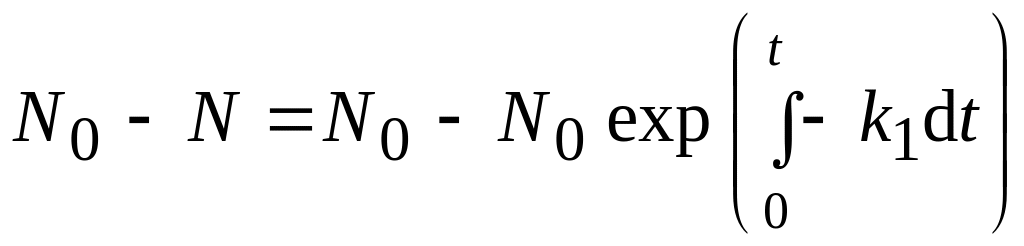следовательно,

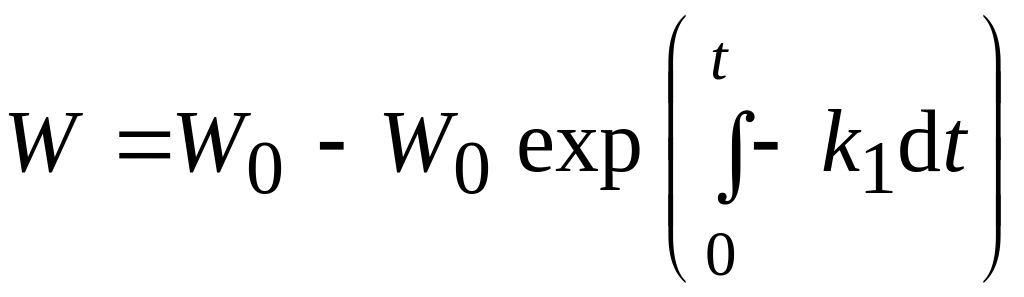, (3.24)

где W₀ – количество побочных продуктов, которое выделилось бы, если бы образовались все возможные химические связи (N₀).

Из (3.24) имеем

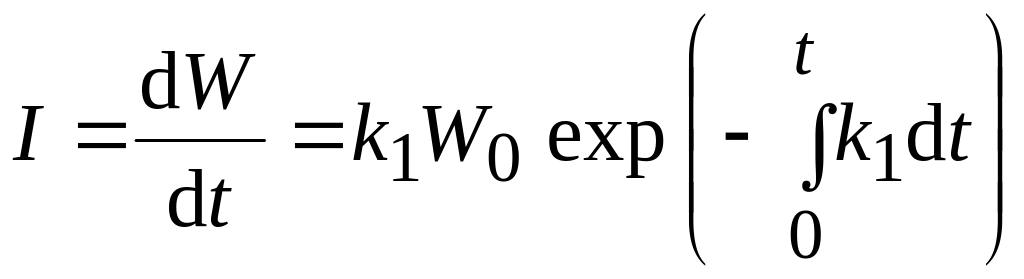. (3.25)

Подставим (3.25) в (3.23):

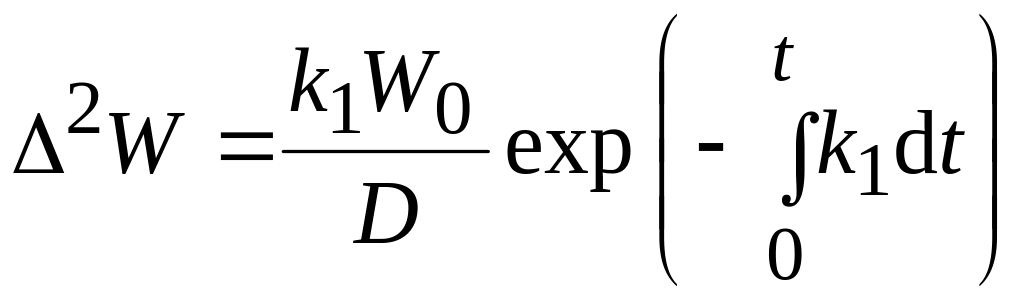, (3.26)

,

где y – координата по толщине.

Решение уравнения (3.26) имеет следующий вид:

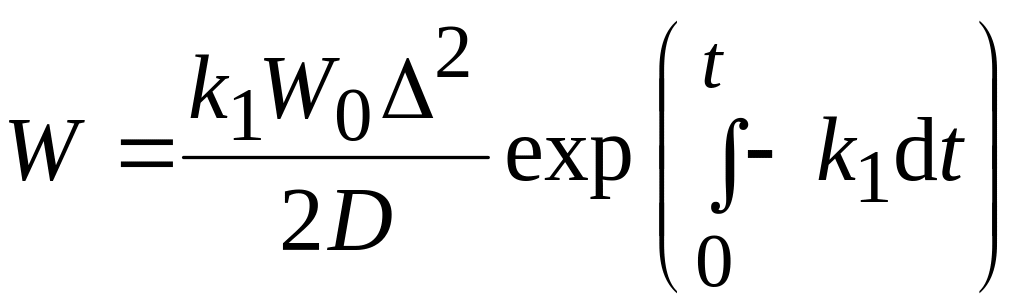, (3.27)

где  – толщина лаковой пленки.

, (3.28)

где U₁ – энергия активации пленкообразования.

, (3.29)

где  – энергия активации удаления побочных продуктов.

Подставим выражения (3.28) и (3.29) в (3.27):

.

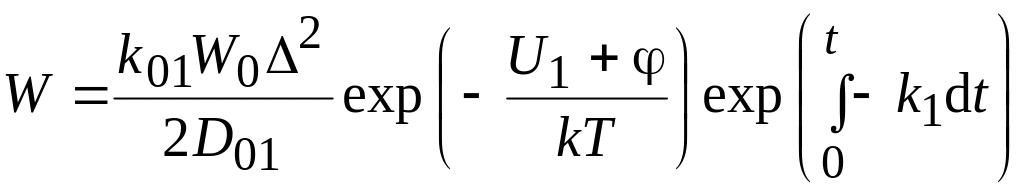Найдем наиболее допустимую температуру, при которой не образуются газовые включения:

Т = Т_н, W = W_доп , t = 0,

где W_доп – допустимая концентрация побочных продуктов, при которой еще не образуются газовые включения;

Т_н – температура начала образования газообразных включений;

t – время образования газообразных включений.

,

.

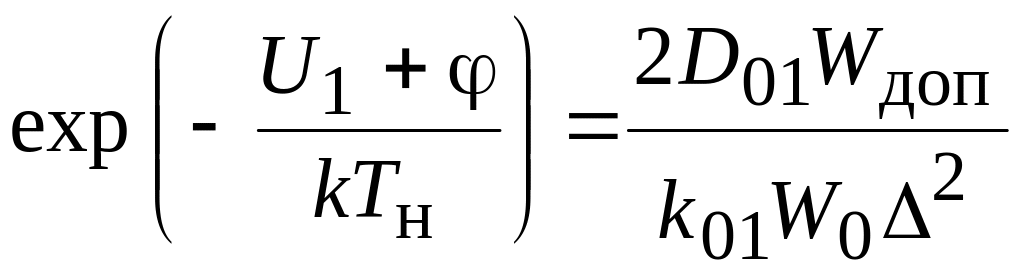Преобразуем это выражение:

.

Обозначим

.

Тогда

.

Откуда

.

Это и есть температура образования газообразных включений на стадии пленкообразования. U₁, b и Р для некоторых эмаль-лаков имеют числовые значения (табл. 3.3).

Таблица 3.3

Значения коэффициентов U₁, b и Р для некоторых типов эмаль-лаков

Тип эмаль-лака	U1,Дж	b	Р, 1/м2
ПЭ-939	1,78∙10–19	1,49	5,92∙1015
ПЭ-999	1,65∙10–19	2,08	1,26∙1014
ИД-9142	1,65∙10-19	2,08	1,26∙1014
УР-9119	1,1∙10-19	1,08	2,78∙1015

Таким образом, для исключения образования пузырей в изоляции эмалированных проводов на стадии пленкообразования необходимо, чтобы максимальная температура провода в процессе эмалирования Т_{пр max} не превышала температуру образования газообразных включений при реакции пленкообразования Т_н.

.

3.6. Расчет температуры эмалируемой проволоки

Тепло к проволоке в эмаль-печи передается путем конвективного теплообмена от воздуха и путем лучеиспускания от стенок печи и нагревателей. Поступившее к проволоке тепло идет на нагрев медной проволоки и изоляции. Исходя из этого, можно написать уравнение теплового баланса:

dQ_к + dQ_из = dQ_м + dQ_пл, (3.30)

где dQ_к – тепло, которое передается проволоке от воздуха эмаль-печи путем конвекции;

dQ_из – тепло, которое передается проволоке от стенок эмаль-печи путем излучения;

dQ_м – тепло, которое идет на нагрев медной проволоки;

dQ_пл – тепло, которое идет на нагрев лаковой пленки.

Тепло, идущее на нагрев проволоки в единицу времени,

dQ_м = _м С_м F dT,

где _м – плотность меди, кг/м³;

С_м – теплоемкость меди, Дж/(кг∙°С);

F – площадь поперечного сечения медной проволоки.

dQ_пл пропорционально dQ_м и учитывается через коэффициент η = 1,03...1,11.

dQ_м + dQ_пл = dQ_м = _м C_м F dT, (3.31)

dQ_к = P_к(Т_в – Т ) dt, (3.32)

где Р – периметр проволоки;

_к – коэффициент конвективной теплоотдачи от воздуха к проволоке;

Т_в – температура воздуха в эмаль-печи;

t – время.

dQ находится из закона Стефана – Больцмана:

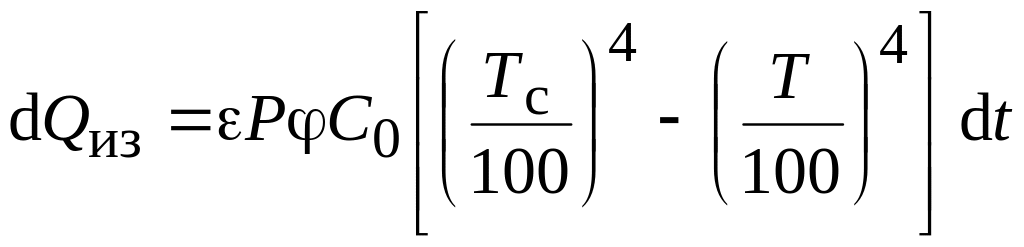, (3.33)

где  – коэффициент облучения проволоки;

С₀ – коэффициент лучеиспускания абсолютно черного тела, С₀ = = 5,7∙10^–8 Вт/(м²∙К⁴);

 – коэффициент черноты проволоки;

Т_с – температура стенки эмаль-печи, К;

– время нагрева на участке dh со скоростью эмалирования V_эм.

Отношение , где d – диаметр проволоки.

Подставим выражения (3.31), (3.32) и (3.33) в (3.30):

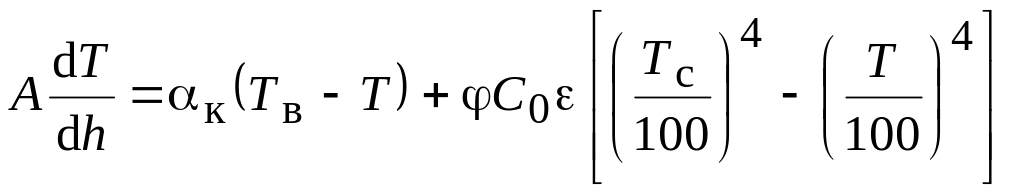, (3.34)

где

.

Так как Т_с и Т_в изменяются по высоте или длине печи, то выражение (3.34) справедливо для каждой точки температурной кривой проволоки.

.

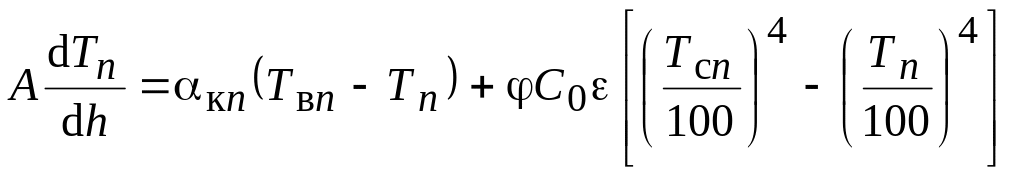Преобразуем это выражение:

,

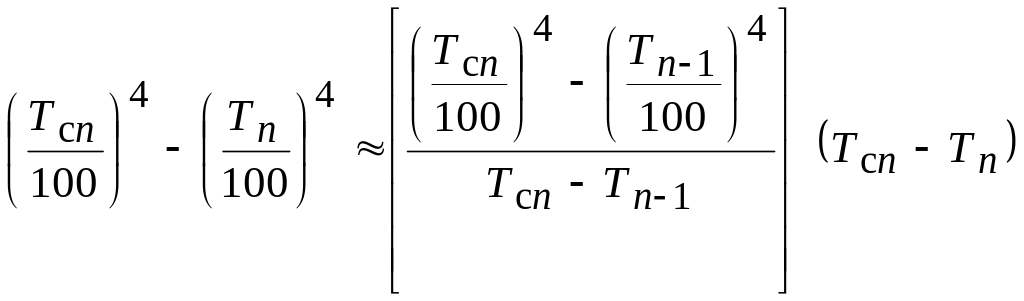где

,

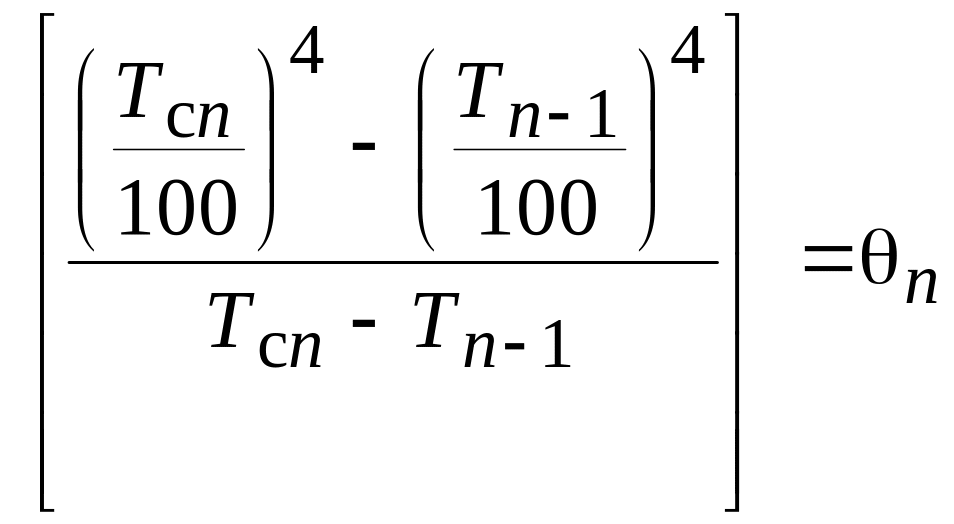тогда

С₀ _n = а_n,

. (3.35)

Проинтегрируем выражение (3.35):

,

,

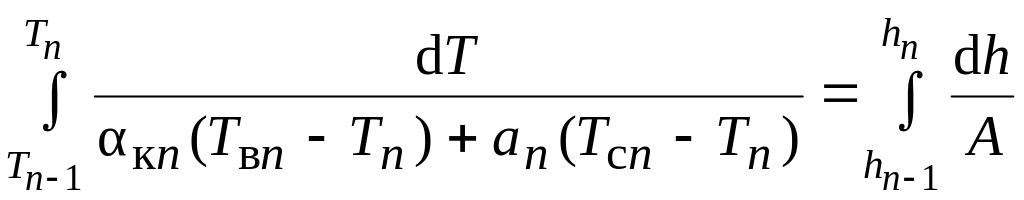обозначим ,

,

откуда

.

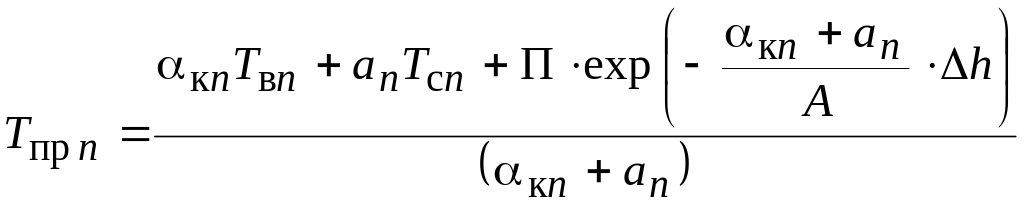Для расчета температуры проволоки T_пр необходимо знать коэффициент черноты проволоки  и коэффициент конвективной теплоотдачи _к;  зависит от толщины эмалированного слоя; _к рассчитывается с помощью критериев Рейнольдса и Нуссельта.

Критерий Рейнольдса

,

где V_вn – скорость воздуха в эмаль-печи относительно проволоки, м/с;

d – диаметр проволоки, м;

_в – кинематическая вязкость воздуха, м²/с.

Критерий Нуссельта связан с критерием Рейнольдса:

Nu = c Re^m,

где с, m – коэффициенты, которые выбираются в зависимости от величины Re (с = 0,43; m = 0,5 для эмалированных проводов).

Критерий Нуссельта можно найти из следующего выражения:

,

где _в – теплопроводность воздуха, Вт/(м∙°С).

При эмалировании проводов на эмаль-агрегатах с каталитическим сжиганием газов и рекуперацией тепла в первой половине эмаль-печи направление воздушного потока совпадает с направлением движения проволоки, а во второй половине печи воздушный поток направлен против движения проволоки.

V_вn = |V_эм – V_в|, если направления воздушного потока и движения проволоки совпадают.

V_вn = V_эм – V_в, если эти направления противоположны.

Обычно в эмаль-печи известна V_в только в первой точке, т.е. V₀ при температуре Т₀.

Зная эти величины, можно рассчитать скорость воздуха в любой точке печи:

.

При измерении температуры воздуха в эмаль-печи термопарой можно приближенно считать, что _пр = _т и _пр = _т. Тогда температуру проволоки можно рассчитать по формуле:

где а_1n =  _пр С₀_1n;

.