2.3. Hiperbolik tipli tənliklər üçün sərhəd məsələlərinin dəyişənləri ayırma (Furye) üsulu ilə həlli

Dəyişənləri ayırma üsulu və ya Furye üsulu xüsusi törəməli diferensial tənliklərin həlli üçün tətbiq olunan ən çox yayılmış üsullardan biridir. Bu üsulu hiperbolik tipli tənliklər üçün bircins və qeyri-bircins sərhəd məsələlərinin həllinə tət­biq edəcəyik.

Məsələ 2.8. Ucları bərkidilmiş uzunluqlu bir­cins simin başlanğıc profili və nöqtələrinin başlanğıc sürətləri məlumdur və uyğun olaraq, funksiyaları ilə ifadə olunur. Simin sərbəst rəqslərini ifadə edən funksiyanı tapmalı.

Həlli. Göstərmişdik ki, bu məsələ riyazi şəkildə aşağıdakı kimi qoyulur:

(2.45)

(2.46)

(2.47)

(2.48)

(2.49)

şərtlərini ödəyən u(x,t) funksiyasını tapmalı ( ).

(2.45) tənliyi xətti və bircinsdir, ona görə də xüsusi həllərin cəmi də tənliyin həlli olur.

Əvvəlcə (2.45) tənliyinin (2.48) – (2.49) sərhəd şərtlərini ödəyən və

(2.50)

şəkildə göstərilə bilən sıfırdan fərqli (qeyri-trivial) həllini tapaq. Həllin (2.50) şəklini (2.45) tənliyində yerinə yazsaq və alınan bərabərliyin hər iki tərəfini -ə bölsək

(2.51)

alarıq.

(2.51) bərabərliyinin sağ tərəfi yalnız t dəyişəninin, sol tərəfi isə yalnız x dəyişəninin funksiyasıdır və onun ixtiyari və t >0-da ödənməsi üçün hər iki kəsr eyni bir sabitə bərabər olmalıdır. bu sabiti ilə işarə etsək

olar.

Buradan və funksiyalarını tapmaq üçün

adi diferensial tənliklərini, (2.48) – (2.49) şərtlərindən isə

alırıq.

Aydındır ki,

şərtləri ödənməlidir, əks halda və olardı, biz isə trivial olmayan, yəni eynilik kimi sıfır olmayan həlli axtarırıq. Belləiklə, funksiyasının tapılması üçün aşağıda­kı məsələyə gəlirik:

, (2.52)

(2.53)

yəni -nın elə qiymətlərini tapmalıyıq ki, (2.52) – (2.53) məsələsinin qeyri-trivial həlləri olsun. -nın belə qiymətlərinə məxsusi qiymətlər, onlara uyğun (2.52) – (2.53) məsələsinin həllərinə isə məxsusi funksiyalar deyilir. (2.52) – (2.53) məsələsinə məxsusi ədədlər və məxsusi funksiyalar haqqında məsələ və ya Şturm-Luivill məsələsi deyilir.

Ayrıca olaraq parametrinin mənfi, sıfır və ya müsbət olduğu hallara baxaq.

1. olduqda məsələnin trivial olmayan həlli yoxdur.

Tənliyin ümumi həlli

şəklində olur. Sərhəd şərtlərindən

alınır, yəni

və

alınır.

Baxdığımız halda olduğundan

.

Ona görə də

və deməli,

.

2. olduğu halda da trivial olmayan həll yoxdur. Doğrudan da, bu halda

və sərhəd şərtlərindən alırıq, ona görə də

.

3. halında tənliyin ümumi həllində xəyali üst iştirak edir və həqiqi həlli aşağıdakı kimi yazmaq olar:

,

burada və ixtiyari həqiqi ədədlərdir.

Sərhəd şərtlərindən alırıq:

-in eynilik kimi sıfra bərabər olmaması üçün olmalıdır. Ona görə də

və ya

olmalıdır.

Deməli, (2.52) – (2.53) məsələsinin trivial olmayan həlli yalnız

qiymətlərində ola bilər.

Bu məxsusi qiymətlərə

(2.54)

məxsusi funksiyaları uyğundur.

-in tapılan qiymətlərinə

tənliyinin

(2.55)

həlli uyğundur, burada və ixtiyari sabit əmsallardır.

Beləliklə, (2.45) tənliyinin (2.48) – (2.49) sərhəd şərtlərini ödəyən xüsusi həlləri

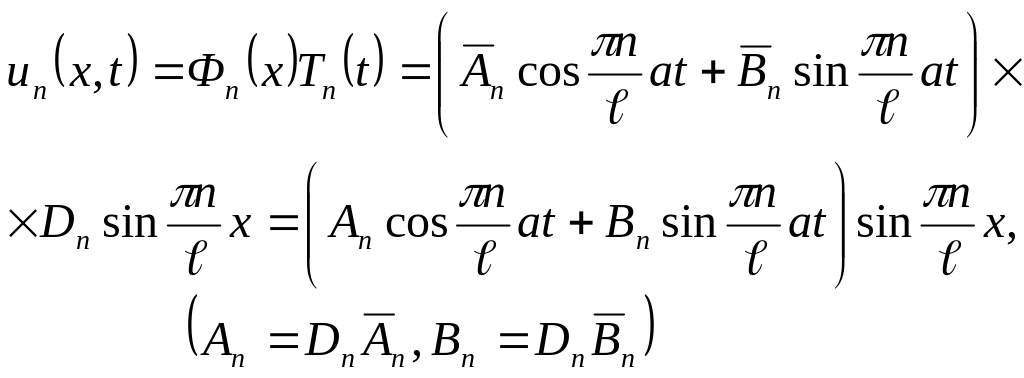(2.56)

kimi olur. (2.45) tənliyi xətti və bircins olduğundan, xüsusi həllərin cəmindən (superpozisiyasından) düzəldilmiş

funksiyası da bu tənliyi və (2.48) – (2.49) sərhəd şərtlərini ödəyir.

Başlanğıc şərtlərdən alırıq:

(2.57)

Furye sıraları nəzəriyyəsindən məlumdur ki, intervalında verilən ixtiyari hissə-hissə kəsilməz və hissə-hissə diferensiallanan funksiyası Furye sırasına ayrılır.

və funksiyaları Furye sırasına ayrılma şərtlərini ödəyirsə, onda bu funksiyaların məxsusi funksiyalara (yəni ) nəzərən Furye sıralarına ayrılışı

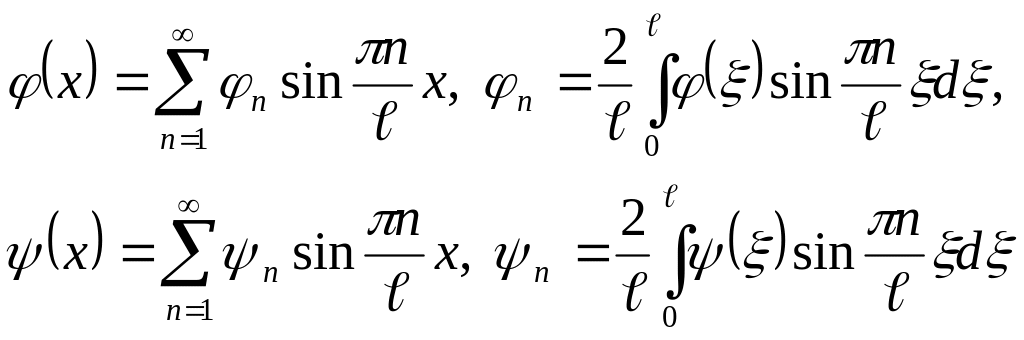
olar.

Bu sıraları (2.57) ifadələri ilə müqayisə etdikdə alırıq ki,

.

Deməli,

(2.58)

Biz həllin formal qurulması ilə kifayətlənirik. (2.58) sırası­nın yığıldığını və həllin varlığı şərtlərini ödədiyini qəbul edəcə­yik.

Alınan həllin fiziki interpretasiasını (izahını) vermək olar. Bunun üçün funksiyalarını

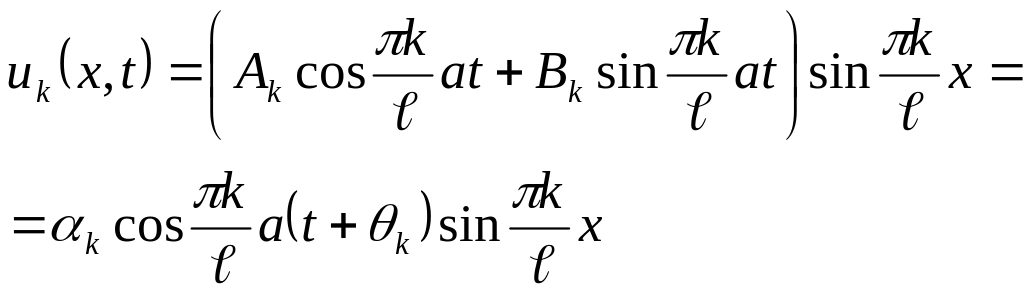
şəklində yazaq, burada .

Simin hər bir nöqtəsi amplitudası olan

harmonik rəqslərini edir. Simin bu tipli hərəkətinə durğun dalğalar və yaxud məxsusi rəqslər, ədədlərinə məxsusi rəqslərin tezlikləri deyilir.

Simin rəqsləri bizə adətən simin verdiyi səs vasitəsi ilə çatdırılır. Simin səsi rəqsin parçalandığı durğun dalğalara uyğun sadə tonların bir-biri üzərinə düşməsindən ibarətdir. Tonun yüksəkliyi bu tona uyğun olan rəqslərin tezliyindən asılıdır. Simin əmələ gətirdiyi ən alçaq ton , ən alçaq məxsusi tezliyi olan

vasitəsi ilə təyin olur və simin əsas tonu adlanır. Qalan tezliklərə uyğun tonları obertonlar adlanır.

Məxsusi dalğaların tezlikləri başlanğıc şərtlərdən asılı deyildir, yəni rəqslərin tezlikləri onların həyəcanlandırılması qaydasın­dan asılı deyildir, tezliklər rəqs edən sistemin (simin) özünü xarakterizə edir və sərhəddəki rejimdən asılı olur.

Məsələ 2.9. Başlanğıc şərtlər ixtiyari olduqda, ucları bər­ki­dilmiş bircins simin kiçik eninə məcburi rəqsləri prosesini ifadə edən funksiyanı tapmalı.

Həlli. Bu halda rəqsləri ifadə edən u(x,t) funksiyası aşa­ğıdakı sərhəd məsələsinin həlli olar:

(2.59)

(2.60)

(2.61)

(2.62)

2.9 məsələsində tapılmış məxsusi ədədlər və məxsusi funksiyalardan istifadə edərək, (2.59) – (2.62) məsələsinin həllini x-ə nəzərən

(2.63)

Furye sırası şəklində axtaracağıq.

u(x,t)-ni təyin etmək üçün u_n(t) funksiyasını tapmaq lazımdır. funksiyalarını Furye sırası şəklində göstərək:

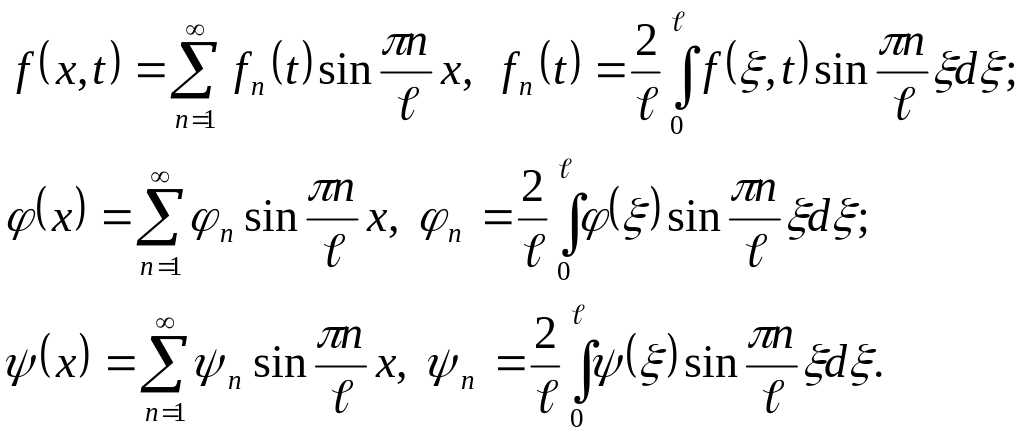(2.64)

Həllin (2.63) ifadəsini (2.59) tənliyində yerinə yazsaq,

alarıq. Buradan görünür ki,

(2.65)

olarsa (2.59) tənliyi ödənər. Başlanğıc şərtlərdən

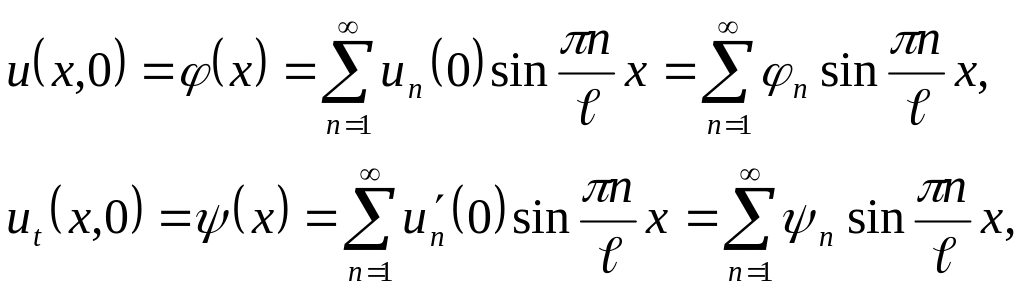
buradan isə

(2.66)

olduğu alınır. Beləliklə, -ni tapmaq üçün adi diferensial tənlik üçün (2.65) – (2.66) Koşi məsələsini almış oluruq.

(2.65) – (2.66) məsələsinin həllini

şəklində göstərmək olar, burada və funksiyaları aşağıdakı şərtləri ödəyir:

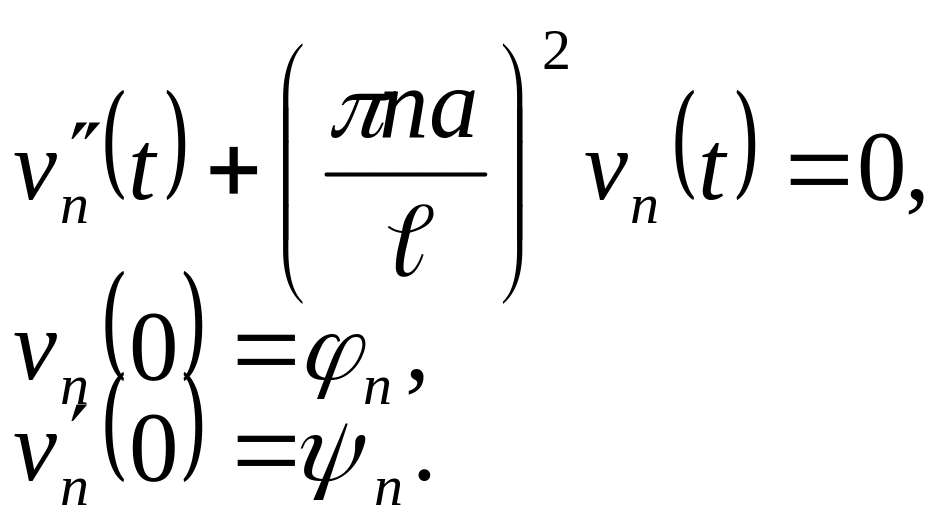(2.67)

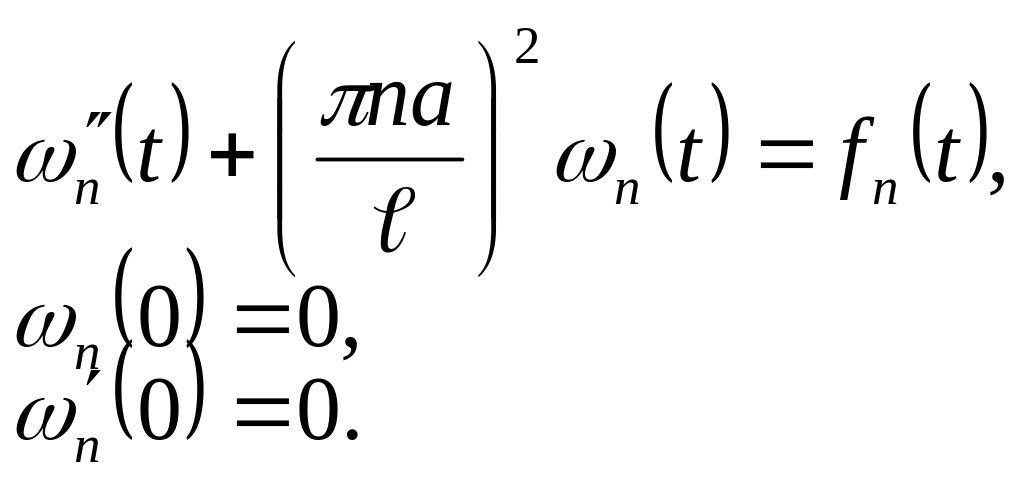(2.68)

(2.67) bərabərliklərindən

və

alınır.

(2.68) məsələsinin ümumi həllini adi diferensial tənliklər fənnindən məlum olan üsullardan, məsələn, sabitlərin variasiyasiya üsulundan istifadə etməklə tapmaq olar.

Göstərmək olar ki, (2.68) məsələsinin həlli

(2.69)

funksiyası olur, burada

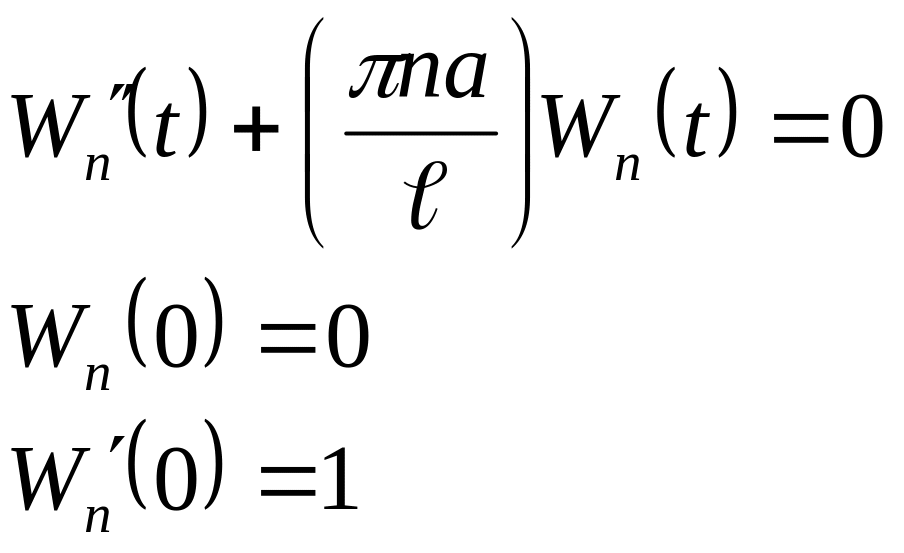(2.70)

şərtlərini ödəyir. (2.70)-dən

və alınan funksiyasını (2.69) bərabərliyində yerinə yazmaqla,

(2.71)

alırıq. Beləliklə,

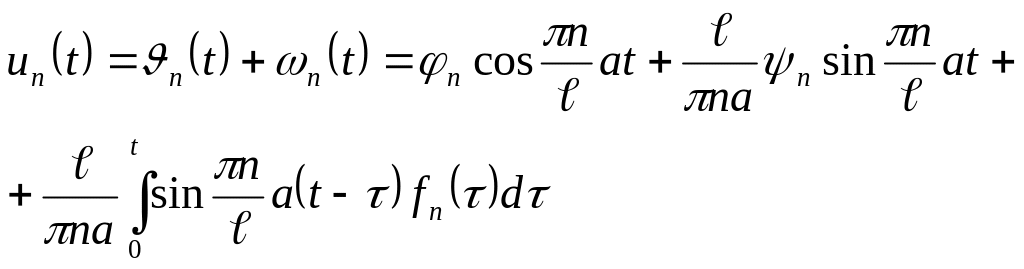
və deməli, axtarılan həll

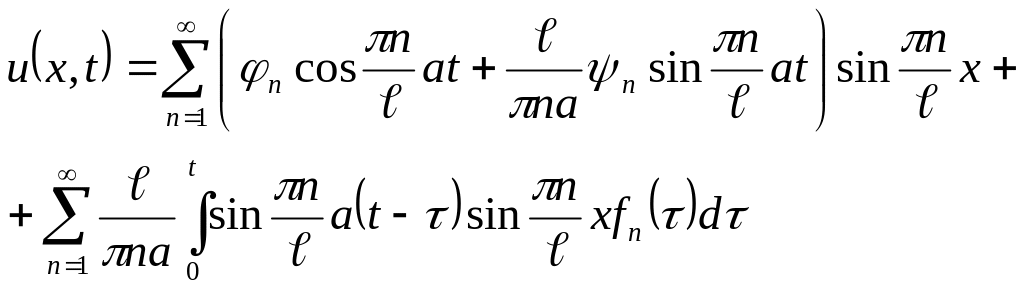(2.72)

şəklində olar.

(2.72) düsturunda birinci cəm simin verilmiş başlanğıc şərtlərini ödəyən sərbəst rəqslərini, ikinci cəm isə xarici qüvvənin təsiri altında simin sıfır bahlanğıc şərtləri daxilində məcburi rəqslərini ifadə edir.

Məsələ 2.10. 2.9-cu məsələni simin ucları verilmiş qa­nun­la hərəkət edən hal üçün həll etməli.

Həlli. Bu halda axtarılan u(x,t) funksiyası rəqslər tənliyi üçün qeyri-bircins birinci sərhəd məsələsinin həlli olur.

, (2.73)

, (2.74)

, (2.75)

, (2.76)

, (2.77)

burada verilmiş kifayət qədər ha­mar (məsələnin həllinin varlığı və yeganəliyi üçün lazım olan şərtləri ödəyən) funksiyalardır və .

(2.73) – (2.77) məsələsinin həllini (2.76) – (2.77) sərhəd şərtlərini ödəyən ixtiyari S(x,t) və yeni məchul funksiyalarının cəmi şəklində axtaraq:

(2.78)

S(x,t) funksiyasını, məsələn, x-ə görə xətti

funksiya şəklində qəbul etməklə a(t) və b(t)-ni şərtlərindən təyin etsək,

(2.79)

alarıq.

(2.78) funksiyası (2.73) – (2.77) məsələsinin şərtlərini ödədiyindən

olmalıdır. Buradan olduğunu nə­zə­rə alsaq, məchul funksiyası üçün aşağıdakı sərhəd mə­sə­ləsini alarıq:

(2.80)

(2.81)

Bununla da funksiaysı üçün ümumi (2.73) – (2.77) sərhəd məsələsi funksiyası üçün sərhəd şərtləri sıfır olan (2.80) – (2.82) məsələsinə gətirilir. Bu məsələnin həll üsulu yuxarıda (məsələ 2.9) şərh edilmişdir.

Beləliklə, 2.9-cu məsələdəki (2.72) düsturundan istifadə etsək (2.73) – (2.77) sərhəd məsələsinin axtarılan həlli

(2.83)

şəklində olar. Burada uyğun olaraq, funksiyalarının məxsusi funksiyalara görə Furye sırası­na ayrılışının əmsallarıdır, yəni

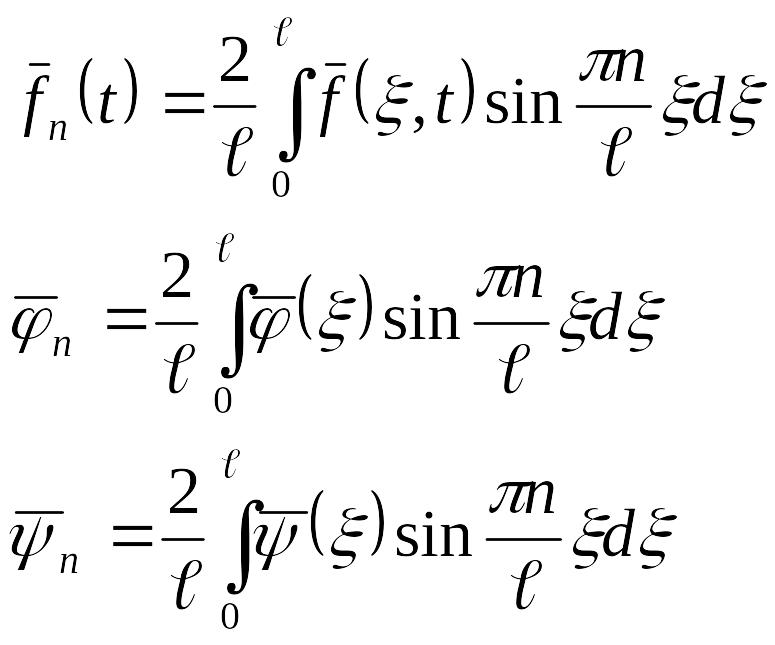
Qeyd. Biz simin rəqs tənliyi üçün I sərhəd məsələsinin Fur­ye üsulu ilə həllini araşdırdıq. Aşkardır ki, digər sərhəd şərt­ləri olan məsələləri də göstərilən üsulla analoji olaraq həll et­mək olar. Bu hallarda sərhəd şərtlərindən asılı olaraq, məx­su­si ədədlər və məxsusi funksiyalar, həmçinin bu şərtləri ödəyən köməkçi S(x,t) funksiyası dəyişəcəkdir.

Furye üsulu çoxölçülü halda (yəni axtarılan funksiya bir neçə fəza dəyişənindən asılı olduqda) hiperbolik tipli tən­lik­lər üçün sərhəd məsələlərinin həllinə də tətbiq oluna bilər. Gös­tə­rilən halları nəzərə alan dəyişənləri ayırma üsulunun ümumi sxemini verməklə kifayətlənək.