§ 7. Ортонормированный базис

Определение 1. Базис евклидова пространства называется ортогональным, если векторы базиса попарно ортогональны, т. е.

при .

Если при этом все векторы базиса единичные, т. е.

то базис называется ортонормированным.

Теорема. Во всяком ‑ мерном евклидовом пространстве имеются ортонормированные базисы.

Доказательство. Доказательство проведем для случая . Пусть ‑ произвольный базис пространства . Докажем, что с его помощью можно построить ортонормированный базис. Положим , где – некоторое вещественное число, которое мы подберем так, чтобы векторы и были ортогональны, то есть

Используя условия 2 и 3 определения евклидова пространства, получим

откуда получим (так как

(3.12)

Итак, если в качестве взять число, определяемое равенством (3.12), то векторы и будут ортогональны, а так как векторы и линейно независимы, то из формулы, определяющей вектор , следует, что он не может стать нулевым. Вектор определим с помощью равенства

, (3.13)

где вещественные числа и определим так, чтобы вектор был ортогонален к векторам и , т. е. чтобы выполнялись равенства

Используя, как и выше, условия 2 и 3 определения евклидова пространства, можем написать

откуда, учитывая ортогональность векторов и (т. е. ), получим выражение для и

. (3.14)

Итак, если в качестве и взять числа, определяемые равенствами (3.14), то вектор будет ортогонален векторам и , так как векторы линейно независимы, то вектор не может быть нулевым (вектор выражается с помощью (3.13) в виде линейной комбинации векторов )

Базис – ортогональный. Но для того чтобы сделать его ортонормированным, следует каждый из векторов поделить на его длину. Векторы

образуют искомый ортонормированный базис.

Для случая этот процесс следует продолжать до тех пор, пока не найдем последний вектор.

Примененный здесь способ получения ортонормированного базиса из произвольного базиса носит название процесса ортогонализации. Естественно, что каждый вектор в -мерном евклидовом пространстве можно представить в виде

. (3.15)

где – некоторый ортонормированный базис, – координаты вектора в этом базисе. Отметим, что для координат имеют место равенства

которые получатся, если умножить обе части равенства (3.15) на .

Задачи.

1. Доказать, что в пространстве со скалярным произведением два вектора и .лежат на одной прямой (т. е. линейно зависимы) тогда и только тогда, когда

2. Доказать, что в пространстве со скалярным произведением два вектора и лежат па одном луче (пли , или при некотором ) тогда и только тогда, когда

3. Доказать, что в евклидовом пространстве два вектора х и у ортого­нальны тогда н только тогда, когда

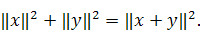
4. Доказать, что в унитарном пространстве два вектора и ортогональны тогда и только тогда, когда для любых комплексных чисел и .

5. Доказать, что в пространстве со скалярным произведением имеет место тождество Аполлония

6. Доказать, что в пространстве со скалярным произведением для любых; четырех векторов справедливо неравенство Птолемея Когда реализуется равенство?

7. В линейном пространстве непрерывных на функций таких, что интеграл сходится, введем скалярное произведение (интеграл понимаем как несобственный) Доказать, что выполнены аксиомы скалярного произведения.

8. В пространстве со скалярным произведением задачи 7 рассмотрим систему . В результате ее ортогонализации по Шмидту получается ортонормированная система многочленов Чебышева — Эрмита. Вычислить три ее первых многочлена.

9. В линейном пространстве непрерывных на функций таких, что интеграл сходится, скалярное произведение введем так: Проверить аксиомы скалярного произведения.

10. В пространстве со скалярным произведением задачи 9 процесс орто-оиализации системы . приводит к системе многочленов Чебышева — Лагерра. Вычислить три первых многочлена этой системы.