
- •Введение.
- •§1. Определение нормированного пространства.
- •§2. Предел последовательности.
- •§3. Неравенства Гёльдера и Минковского для сумм.
- •§ 4. Пространство
- •§ 5. Пространство ограниченных числовых последовательностей т
- •§ 6. Пространство
- •§ 7. Пространство непрерывных функций
- •§ 8. Пространство .
- •§ 9. Пространство
- •Задачи.
§ 5. Пространство ограниченных числовых последовательностей т
Рассмотрим множество
последовательностей ![]() таких, что
таких, что ![]() .
Это множество принято обозначать
буквой
.
Если
.
Это множество принято обозначать
буквой
.
Если ![]() и
и ![]() ,
то
по определению полагают
,
то
по определению полагают
![]()
Упражнение 1.
Доказать, что если ![]() ,
то
,
то ![]() и, значит,
— линейное
пространство.
и, значит,
— линейное
пространство.
Превратим в нормированное пространство, полагая
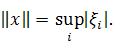
Упражнение 2.
Проверьте справедливость аксиом нормы
в пространстве
.
Какова
сходимость в
?
Пусть ![]() и
.
Это означает,
что для любого
и
.
Это означает,
что для любого ![]() найдется номер
найдется номер ![]() такой, что для любых n
такой, что для любых n
![]() выполняется
выполняется
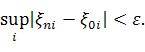
Последнее неравенство
эквивалентно условию, что ![]() для любых номеров
.
для любых номеров
.
Таким образом, сходимость в — покоординатная, равномерная относительно номера координаты.
§ 6. Пространство
Рассмотрим множество
![]() всех числовых последовательностей
всех числовых последовательностей ![]() таких, что ряд
таких, что ряд ![]() сходится.
сходится.
Упражнение 1.
Покажите, что если ![]() ,
то и
,
то и ![]() .
Норму в
введем по формуле
.
Норму в
введем по формуле
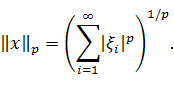
Упражнение 2. Проверьте аксиомы 1) и 2) нормы.
Докажем в
неравенство
треугольника. В неравенстве Минковского
для конечных сумм (4) § 3 увеличим правую
часть, заменив
на любое ![]() ,
и в полученном
неравенстве
,
и в полученном
неравенстве
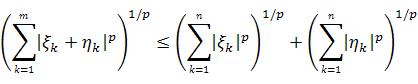
перейдем к пределу
при ![]() .
Получим неравенство (для любых
)
.
Получим неравенство (для любых
)
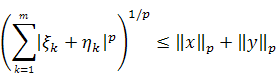
Отсюда следует,
что ряд ![]() сходится,
как ряд с неотрицательными членами,
частичные суммы которого ограничены
(см. учебник по математическому анализу).
Следовательно,
сходится,
как ряд с неотрицательными членами,
частичные суммы которого ограничены
(см. учебник по математическому анализу).
Следовательно, ![]() ,
и справедливо нопавелство
,
и справедливо нопавелство
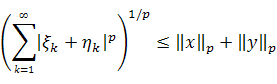
Это и есть неравенство треугольника. Итак, — нормированное пространство.
§ 7. Пространство непрерывных функций
Рассмотрим линейное
пространство всех непрерывных на ![]() функций.
Норму введем так:
функций.
Норму введем так:
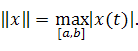
Аксиомы 1) и 2) нормы
проверяются тривиально. Проверим аксиому
3). По свойству модуля для любого ![]() имеем
имеем
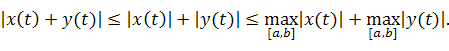
Следовательно,
![]() .
Неравенство
сохранится, если взять
.
Неравенство
сохранится, если взять ![]() в левой его части. В результате получаем
неравенство треугольника для нормы в
в левой его части. В результате получаем
неравенство треугольника для нормы в
![]() ;
для полученного
нормированного пространства мы сохраним
прежнее обозначение.
;
для полученного
нормированного пространства мы сохраним
прежнее обозначение.
Покажем теперь,
что сходимость по норме в
есть равномерная
сходимость. Пусть дана последовательность
![]() ,
и пусть она
сходится к
,
и пусть она
сходится к ![]() ,
т. е.
,
т. е. ![]() .
Это означает следующее: для любого
.
Это означает следующее: для любого ![]() существует номер
существует номер ![]() такой, что
при любых
такой, что
при любых ![]() справедливо
неравенство
справедливо
неравенство
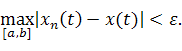
и тем более ![]() для всех
.
Итак, сходимость
по норме в
— равномерная.
для всех
.
Итак, сходимость
по норме в
— равномерная.
Посмотрим, как
выглядит в
(в вещественном случае) окрестность
![]() .
Для этого построим графики функций
.
Для этого построим графики функций ![]() .
Эти два
графика и отрезки прямых
.
Эти два
графика и отрезки прямых ![]() и
и ![]() ограничивают
ограничивают
![]() - полоску (полоску ширины
- полоску (полоску ширины ![]() вокруг графика
вокруг графика ![]() ,
которая и
служит
-окрестностью точки
(рис. 1).
,
которая и
служит
-окрестностью точки
(рис. 1).
Рис. 1.
В ![]() лежат те элементы
лежат те элементы ![]() ,
графики
которых лежат строго между графиками
элементов
,
графики
которых лежат строго между графиками
элементов ![]() и
и ![]() .
.
§ 8. Пространство .
В линейном
пространстве
раз непрерывно
дифференцируемых на ![]() функций
введем норму
функций
введем норму
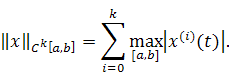
где ![]() — производная функции
— производная функции ![]() .
.
Упражнение.
Проверьте аксиомы нормы в ![]() .
Покажите,
что сходимость в
— это
равномерная сходимость на
последовательностей
.
Покажите,
что сходимость в
— это
равномерная сходимость на
последовательностей
![]() .
.
§ 9. Пространство
Вернемся к линейному пространству непрерывных на функций. Однако теперь мы введем норму иначе:
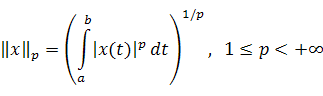
(интегрирование понимается в смысле Римана).
Упражнение 1. Проверьте аксиомы 1) и 2) нормы. Аксиома треугольника представляет собою неравенство Минковского для интегралов:
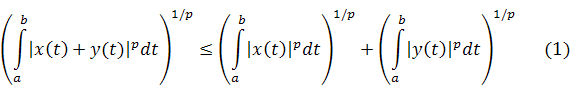
Доказательство неравенства Минковского при основывается на неравенстве Гёльдера
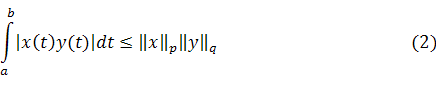
где  .
Заметим сначала, что если
.
Заметим сначала, что если ![]() на
или
на
или ![]() на
,
то неравенство
(2) справедливо. Пусть
на
,
то неравенство
(2) справедливо. Пусть ![]() .
Подставим в неравенство (см. (2) § 3)
.
Подставим в неравенство (см. (2) § 3) 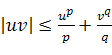 следующие
выражения
следующие
выражения 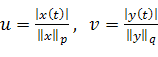 и, проинтегрировав
получившееся неравенство, получим
и, проинтегрировав
получившееся неравенство, получим
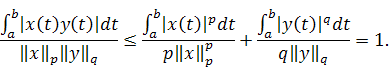
Это и есть неравенство (2).
Далее, имеем, как и в случае сумм (см. § 3),
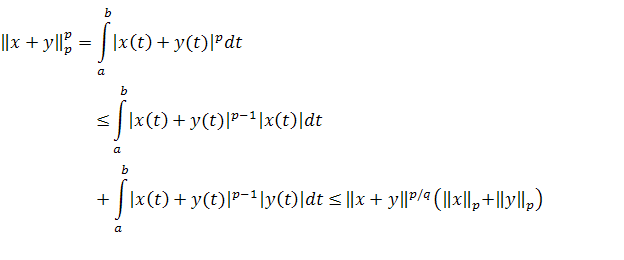
После сокращения
на ![]() получаем
неравенство Минковского (1).
получаем
неравенство Минковского (1).
Определение 1.
Пусть в линейном пространстве
введены две
нормы: ![]() и |
и |![]() .
Если существует постоянная
.
Если существует постоянная ![]() такая, что для любых
выполнено неравенство
такая, что для любых
выполнено неравенство
![]()
то будем говорить, что норма подчинена норме .
Упражнение 2.
Покажите, что если в линейном пространстве
заданы ![]() и
и ![]() ,
причем
подчинена
,
то из сходимости последовательности
,
причем
подчинена
,
то из сходимости последовательности
![]() в смысле
вытекает ее сходимость в смысле
,
причем к тому же элементу.
в смысле
вытекает ее сходимость в смысле
,
причем к тому же элементу.
Определение 2.
Сходимость в ![]() называется
сходимостью
в среднем.
называется
сходимостью
в среднем.
Упражнение 3.
Покажите, что ![]() подчинена норме
подчинена норме ![]() и что, таким образом, из равномерной
сходимости последовательности непрерывных
на
функций следует сходимость ее в среднем
на
.
Возникает
вопрос — верно ли обратное: будут ли
оба введенных вида сходимости
эквивалентны?
и что, таким образом, из равномерной
сходимости последовательности непрерывных
на
функций следует сходимость ее в среднем
на
.
Возникает
вопрос — верно ли обратное: будут ли
оба введенных вида сходимости
эквивалентны?
