1. Теорема Ролля

Знание производной некоторой функции позволяет судить о характерных особенностях в поведении этой функции. В основе всех таких исследований лежат некоторые простые теоремы, называемые теоремами о среднем в дифференциальном исчислении.

Начнем рассмотрение таких теорем с теоремы, связываемой с именем французского математика Ролля (1652–1719).

Теорема 1.1. Если функция   непрерывна на отрезке  , дифференцируема во всех его внутренних точках, а на концах отрезка  ,   обращается в ноль, то существует, по крайней мере, одна точка  , в которой  .

Доказательство. Так как функция непрерывна на отрезке  , то, согласно свойству 11.1.1, она должна достигать хотя бы один раз на этом отрезке своего минимума   и максимума   (рис. 1.1).

Если  , функция постоянна, то есть  . Но в этом случае   для любого  .

В общем случае  , и хотя бы одно из этих чисел не равно нулю. Предположим для определенности, что  . Тогда существует точка  , в которой  .

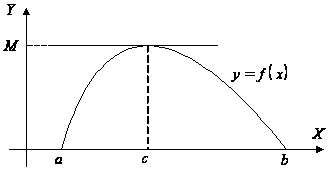
Рис. 1.1

Так как рассматриваемое значение   является максимальным, то для него справедливо, что   для   и  .

Рассмотрим пределы

 для 

и

 для  .

Так как оба предела равны производной функции   в одной и той же точке  , то они равны между собой. Значит, из одновременности   и  следует, что  , что и требовалось доказать.

Следует отметить, что данная теорема справедлива и в том случае, когда на концах отрезка   функция не обращается в ноль, но принимает равные значения  . Доказательство проводится аналогично.

Геометрический смысл данной теоремы следующий: если непрерывная кривая пересекает ось   в двух точках  ,   или принимает в них равные значения, то, по крайней мере, в одной точке между   и   касательная к кривой параллельна оси  .

Необходимо отметить, что если не во всех точках   у рассматриваемой функции существует производная, то теорема может не выполняться. Это касается, например, функции  (рис. 1.2):

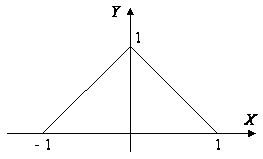
Рис. 1.2

Данная функция непрерывна на отрезке   и обращается в ноль на его концах, но ни в одной точке внутри отрезка производная не равна нулю.

2. Теорема Лагранжа

Результаты теоремы Ролля используются при рассмотрении следующей теоремы о среднем, принадлежащей Лагранжу (1736–1813).

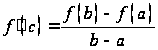Теорема. Если функция   непрерывна на отрезке   и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка  , в которой  .Доказательство. Рассмотрим график функции   (рис. 2.1).

Проведем хорду, соединяющую точки   и  , и запишем ее уравнение. Воспользовавшись уравнением прямой, проходящей через две точки на плоскости, получим:

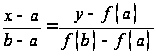,откуда:

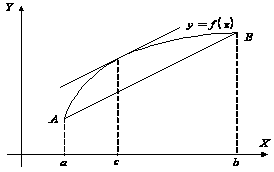
Рис. 2.1

 и  .Составим теперь вспомогательную функцию, вычтя из уравнения кривой уравнение хорды:

.Полученная функция   непрерывна на отрезке   и дифференцируема во всех его внутренних точках. Кроме того, вычисление   в точках   и   показывает, что  . Значит, функция   на отрезке   удовлетворяет требованиям теоремы Ролля. Но в этом случае существует такая точка  , в которой .

Вычислим производную функции  :

Согласно теореме Ролля в точке   производная  , то есть 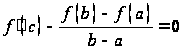  и

,

что и требовалось доказать.

Геометрический смысл теоремы Лагранжа следующий: внутри отрезка   существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при   теорема переходит в теорему Ролля.

Теорему Лагранжа часто записывают в следующем виде:

,

то есть приращение функции равно приращению аргумента, умноженному на производную функции в некоторой внутренней точке. В связи с этим теорему Лагранжа называют также теоремой о конечных приращениях.

Возрастание и убывание функции

        функция y = f (x) называется возрастающей на отрезке [a, b], если для любой пары точек х и х', а ≤ х < х' ≤ b выполняется неравенство f(x) ≤ f (x'), и строго возрастающей — если выполняется неравенство f (x) < f (x'). Аналогично определяется убывание и строгое убывание функции. Например, функция у = х² (рис., а) строго возрастает на отрезке [0,1], а

         

        (рис., б) строго убывает на этом отрезке. Возрастающие функции обозначаются f (x)↑, а убывающие f (x)↓. Для того чтобы дифференцируемая функция f (x) была возрастающей на отрезке [а, b], необходимо и достаточно, чтобы её производная f'(x) была неотрицательной на [а, b].

         Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x) называется возрастающей в точке x₀, если найдётся такой интервал (α, β), содержащий точку x₀, что для любой точки х из (α, β), х> x₀, выполняется неравенство f (x₀) ≤ f (x), и для любой точки х из (α, β), х< x₀, выполняется неравенство f (x) ≤ f (x₀). Аналогично определяется строгое возрастание функции в точке x₀. Если f'(x₀) > 0, то функция f (x) строго возрастает в точке x₀. Если f (x) возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.

экстремумы

Находим производную функции Приравниваем эту производную к нулю Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль) Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную. Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом. Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.

Правило Лопиталя, при ∞ / ∞.

Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x₀ (кроме точки x₀), в этой окрестности

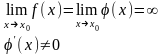
Если существует предел

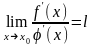, то

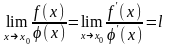
Неопределенности вида 0∙∞ ; ∞-∞ ; 1^∞ ; ∞⁰ ; 0⁰ сводятся к двум основным.

Например, 0∙∞

Пусть f(x)→0, φ(x)→∞ при х→х₀

Выпуклость вогнутость Пусть f(x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f(x). Кривая, заданная функцией y = f(x), называется выпуклой на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.  Кривая называется вогнутой на интервале (a, b), если все точки кривой лежат выше любой ее касательной на этом интервале.  Точка кривой M₀(x₀, f(x₀)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба. Кривая y = f(x) (рис. 2.14) является выпуклой на интервалах (–2; –1,5) и (0; 1,5), вогнутой на интервалах (–1,5; 0) и (1,5; 2). Точки M₁(–1,5; f(–1,5)), O(0, 0),  M₂(1,5; f(1,5)) – точки перегиба. Теорема 1. (Достаточные условия выпуклости и вогнутости графика функции). Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f''(x) < 0, то кривая y = f(x) на этом интервале выпукла. Если во всех точках интервала (a, b):  (x) > 0, то кривая y = f(x) на этом интервале вогнута. Теорема 2 (достаточное условие точки перегиба) Пусть кривая является графиком функции y = f(x). Если  (x₀) = 0 или  (x₀) не существует и при переходе через x₀ вторая производная  (x) меняет свой знак, то точка M₀(x₀, f(x₀)) этой кривой является точкой перегиба. асимптоты

Вертикальные асимптоты. Прямая x = a является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно из условий:

или

(при этом функция f(x) может быть вообще не определена соответственно при

и

).

Замечание. Символом

о бозначается стремление x к a справа, причём x остаётся больше a, символом

стремление x к a слева, причём x остаётся меньше a.

Из сказанного следует, что вертикальные асимптоты кривой нужно искать в точках разрыва и на границах области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет.

Горизонтальные асимптоты. Если

то y = b – горизонтальная асимптота кривой y = f(x) (правая при  , левая при  и двусторонняя, если пределы при  равны).

Наклонные асимптоты. Существование наклонной асимптоты определяется следующей теоремой.

Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b, необходимо и достаточно, чтобы существовали конечные пределы

          (33)

или

      (34)

В первом случае получается правая наклонная асимптота, во втором – левая. Правая наклонная асимптота изображена на рис. 13.

П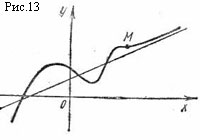 ри совпадении пределов (33) и (34) прямая y = kx + b является двусторонней асимптотой кривой.

Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).

Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0.

Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

Первообразные

     Основные свойства

     1.     

     2.     

     3. Если   то

     4. 

 дробно-рациональные функции интегрируются

Определение 1. Функция вида , где   и  - многочлены, называется дробно-рациональной функцией. Мы будем рассматривать, как правило, правильные дроби, то есть дроби  , где степень многочлена в числителе меньше степени многочлена, стоящего в знаменателе.

Начнем с дробей, в которых в знаменателе стоит квадратный трехчлен.

Обычно дробно-рациональные функции интегрируются с помощью разложения на простейшие дроби.

.

Здесь подынтегральная функция следующим образом раскладывается на простейшие дроби:

= .

Получаем систему:

Решая ее, получаем   значит  = .

Для интегрирования иррациональной функции, содержащей   используется подстановка  . Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме  , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию.  Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида  , интегрируется с помощью подстановки  .  Интегрирование иррациональных функций, содержащих   и  , рассматривается на странице 

Определённый интеграл

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).

Определенный интеграл был введен для ограниченных на отрезке функций. Естественно распространить это понятие на случай бесконечных промежутков и бесконечно больших функций.

Пусть f (x) определена при x ≥ a и интегрируема на отрезке [a; ξ], где ξ ≥ a. Если существует конечный предел 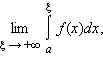  то говорят, что функция f интегрируема в несобственном смысле на промежутке [a; +∞), а несобственный интеграл  сходится: 

Если   не имеет конечного предела при ξ → +∞, то говорят, что несобственный интеграл расходится.

Аналогично определяется несобственный интеграл 

Операционное исчисление

     Преобразование Лапласа 

(f - оригинал; F - изображение).

     Запись 

     Условия на оригинал 

     1. 

     2. f - кусочно-непрерывна на R.

     3.   такие, что 

     Линейность 

     Теорема подобия 

     Если   то 

     Теорема запаздывания 

     Если   то 

     Теорема смещения 

     Если   то 

Дифференцирование оригинала 

     Если   - оригинал, то

     Если   - оригинал, то

Интегрирование тригонометрических выражений

 Универсальная тригонометрическая подстановка

Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными sin x и cos x, над которыми выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать R(sin x;cos x), где R - знак рациональной функции.