24. Гипербола. Определение. Вывод канонического уравнения.

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂=±2a,

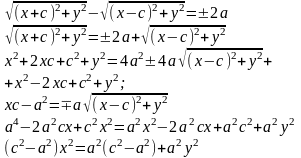
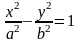
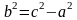
25. Парабола. Определение. Вывод канонического уравнения.

Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0.

Пусть M(x;y) – произвольная

точка M с F. Проведем отрезок

MN перпендикулярно

директрисе. Согласно

определению MF=MN.

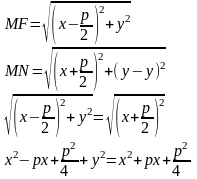
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

1) эллипсоиды  — эллипсоиды,  — мнимые эллипсоиды;   2) гиперболоиды:   — однополостные гиперболоиды,  — двуполостные гиперболоиды;   3) параболоиды (p > 0, q > 0):  — эллиптические параболоиды,   — гиперболические параболоиды;   4) конусы второго порядка:  — конусы,  — мнимые конусы;   5) цилиндры второго порядка:   — эллиптические цилиндры,  — мнимые эллиптические цилиндры,  — гиперболические цилиндры,   — параболические цилиндры.

Приведение общих уравнений кривых к канон

    Приведение уравнения второго порядка к каноническому виду.

 

Определение 11.9. Линия, определяемая общим уравнением второго порядка

              ,                                             (11.5)

называется алгебраической линией второго порядка.

Для квадратичной формы   можно задать матрицу

                   .                                                                                  (11.6)

   Для того, чтобы перейти к новой системе координат, в которой уравнение линии будет иметь канонический вид, необходимо провести два преобразования:

1)       поворот координатных осей на такой угол, чтобы их направление совпало с направлением осей симметрии кривой (если она имеет две оси);

2)       параллельный перенос, при котором начало координат совмещается с центром симметрии кривой (если он существует).

Замечание. Для параболы новые оси координат должны располагаться параллельно и перпендикулярно директрисе, а начало координат – совпасть с вершиной параболы.

  Поскольку в канонических уравнениях кривых второго порядка отсутствуют произведения переменных, необходимо перейти к координатной системе, определяемой базисом из ортонормированных собственных векторов матрицы А. В этом базисе уравнение (11.5) примет вид:

                (в предположении, что λ_1,2 не равны 0).

Зададим последующий параллельный перенос формулами:

              . Получим в новой координатной системе уравнение

                                              .                                                     (11.7)

Рассмотрим возможные геометрические образы, определяемые этим уравнением в зависимости от знаков λ₁, λ₂ и  :

1)       если собственные числа матрицы А λ₁ и  λ₂  и  одного знака, уравнение (11.7) представляет собой каноническое уравнение эллипса:

                                , где       

(случаи   и  , имеющего знак, противоположный знаку λ₁, λ₂, будут рассмотрены в следующей лекции).

2)       если λ₁ и  λ₂  имеют разные знаки, уравнение (11.7) является каноническим уравнением гиперболы:

   или     , в зависимости от знака  .

В случае, когда одно из собственных чисел матрицы А равно 0, уравнение (11.5) в результате двух преобразований координат можно привести к виду:

                               ,                                                                              (11.8)

являющимся каноническим уравнением параболы.

Решение систем линейных уравнений методом Крамера. Пусть нам требуется решить систему линейных алгебраических уравнений 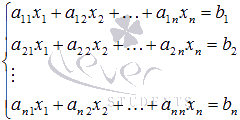  в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть,  . Пусть   - определитель основной матрицы системы, а   - определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов: 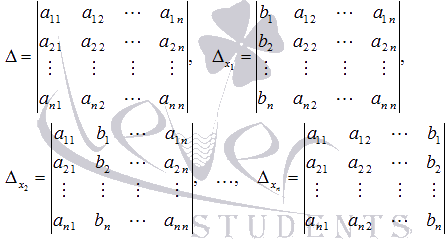  При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как  . Так находится решение системы линейных алгебраических уравнений методом Крамера. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с   неизвестными (над произвольным полем):

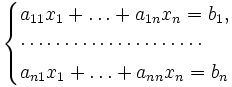
Тогда её можно переписать в матричной форме:

, где   — основная матрица системы,   и   — столбцы свободных членов и решений системы соответственно:

Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.

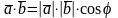
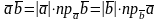
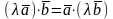
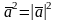
Функции предел

Число А называется пределом функции y=f(x) в точке х₀, если для любой последовательности допустимых значений аргумента x_n, n€N (x_n≠x₀), сходящейся к х₀

(т.е. ), последовательность соответствующих значений функции f(x_n), n€N, сходится к числу А, т.е. 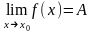. Геометрический смысл предела этой функции, что для всех точек х, достаточно близких к точке х₀, соответствующие значения функции как угодно мало отличается от числа А.

Односторонние пределы.

Считается, что х стремится к х₀ любым способом: оставаясь меньшим, чем х₀ (слева от х₀), большим, чем х₀ (справа от х₀), или колеблясь около точки х₀.

Число А₁ называется пределом функции y=f(x) слева в точке х₀, если для любого ε<0 существует число σ=σ(ε)>0 такое, что при х€(x₀-σ;x₀), выполняется неравенство |f(x)-A₁|<ε

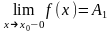
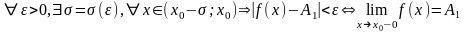
Пределом функции справа называется

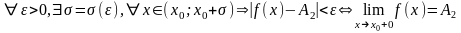
Свойства пределов.

1) если предел 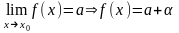функция равна этому числу плюс б.м.

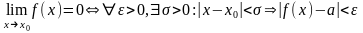
ε – сколь угодно малое число

|f(x)-a|=α; f(x)=a+ α

2) сумма конечного числа б.м. чисел есть б.м. число

3) предел произведения равен произведению пределов

4) константы можно выносить за знак предела

5)

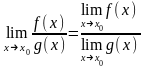
Бесконечно малые.

Переменная   называется бесконечно малой, если для любого   существует такое значение   , что каждое следующии за ним значение   будет по абсолютной величине меньше   .

Если   - бесконечно малая то говорят, что   стремится к нулю, и пишут:   .

Бесконечно большие.

Переменная x называется бесконечно большой, если для всякого положительного числа cсуществует такое значение   , что каждое следующее за ним x будет по абсолютной величине больше   . Пишут: 

Величина, обратная к бесконечно большой, есть величина бесконечно малая, и обратно. 

1)	.
2)	.
3)	.
4)	.
5)	.
6)	(  ).
)	.
7)	(  ).
)	.

непрерывность функции

Пусть функция f(x) определена в некоторой окрестности O(x₀) точки x₀ (включая саму точку x₀).

Функция f(x) называется непрерывной в точке x₀, если существует lim_x → x0 f(x) , равный значению функции f(x) в этой точке:

lim x → x0  f(x) = f(x0),

  Пусть переменная  x  стремится к  a, оставаясь больше  a, и при этом   . Тогда число  A  называют правосторонним пределом (или пределом справа) функции     и обозначают любым из символических выражений

Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае     при  x → a  со стороны меньших значений:

Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.  Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

Существуют левосторонний предел   и правосторонний предел  ;

Эти односторонние пределы конечны.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. 

Производные и дифференциалы высших порядков

Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производнойфункции f и обозначается f". Таким образом,

f"(x) = (f'(x))'.

Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f⁽ⁿ⁾. Итак,

f⁽ⁿ⁾(x) = (f^(n-1)(x))',   n ϵ N,   f⁽⁰⁾(x) = f(x).

Число n называется порядком производной.

Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,

dⁿf(x) = d(d^n-1f(x)),   d⁰f(x) = f(x),   n ϵ N.

Если x - независимая переменная, то

dx = const   и   d²x = d³x = ... = dⁿx = 0.

В этом случае справедлива формула

dⁿf(x) = f⁽ⁿ⁾(x)(dx)ⁿ.

ДИФФиринциал

Производная функции f(x) есть некоторая функция f ’(x), произведенная из данной функции.Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале. Для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. .

Рассмотрим функцию, заданную параметрически: x = φ(t), y = ψ(t). Покажем, что для нахождения производной y'_x, совсем необязательно находить выражение явной зависимости yот x.

Теорема 12. Пусть функция x = φ(t) имеет обратную функцию t = Ф(x). Если функцииx=φ(t), y = ψ(t) дифференцируемы и φ'(t) ≠ 0, тогда : 

Диффиринциал Производной функции γ=f(x) называется функция f'(x), равная пределу отношения приращения функции f(x) к приращению аргумента, когда последнее произвольным образом стремится к нулю:

где ?х - приращение аргумента х.

Производная функция у обозначается также через у' и 

Если функция γ=f(x) изображается кривой в декартовых координатах, то γ' при рассматриваемом значении аргумента выражает угловой коэффициент касательной к кривой в соответствующей точке, т. е. γ'=tg α, где α - угол наклона касательной к оси X. Производная имеет не только геометрическое толкование, она выражает скорость изменения функции относительно аргумента, например скорость движения, интенсивность нагрузки, силу тока, теплоемкость и т. п.

Если функция имеет в рассматриваемой точке производную, то она в этой точке непрерывна; таким образом, непрерывность является необходимым условием существования производной, но это условие не является достаточным, так как непрерывность не гарантирует существования производной. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.  Обозначается dy или df(x).Из определения следует, что dy = f(x)x илиdy = f(x)dx.Можно также записать: 

Замечательные пределы 1)  ; (Первый замечательный предел)

2)  (Второй замечательный предел)Данный предел относят обычно к неопределенностям вида 1^∞. Раскрытие подобных неопределенностей как правило, связано с использованием второго замечательного предела.
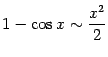