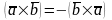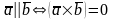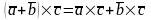Определители. При транспонировании (замене строк определителя на соответствующие столбцы) определитель не изменится.

2. Разложение определителя по любой строке или любому столбцу: определитель равен сумме произведения элементов любого ряда на их алгебраические дополнения.3. При перестановке двух строк или столбцов абсолютная величина определителя не изменится, а знак определителя меняется на обратный.4. Общий множитель строки или столбца можно вынести за знак определителя.5. Свойство линейного преобразования в определителе . Определитель не изменится, если к какой- либо строке (столбцу) прибавить другую строку (столбец) предварительно

умноженную на какое- либо число.6. Если элементы одной строки равны элементам другой строки определителя, то определитель равен нулю .

Определителем называется число, записанное в виде квадратной таблицы:

 .

 

Таблица ограничивается слева и справа вертикальными линиями,   -называется элементами определителя (   -номер строки,   -номер столбца).

Главная диагональ определителя содержит элементы   , противоположная диагональ называется побочной.

Порядком определителя называется число строк (столбцов) квадратной таблицы.

Определитель II порядка вычисляется по формуле:

Определитель III порядка можно вычислить по правилу Сарруса:

оПРЕДЕЛЁННЫЙо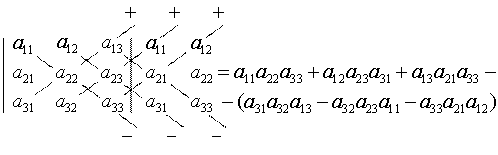

Матрицы Матрицей называется прямоугольная таблица чисел, сод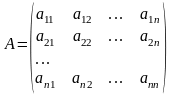 ержащая m строк одинаковой длины.Матрицы равны между собой, если равны все их соответствующие элементы.

Матрица, у которой число строк и столбцов равно – называется квадратной.

Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной.

Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е.

Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной.

Матрица, у которой все элементы равны нулю, называется нулевой.

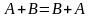
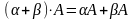
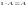
Операция умножения возможна, если количество столбцов первой матрицы равно количеству строк другой матрицы.

где

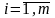
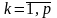
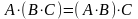
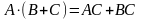
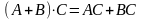
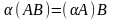
5. Обратная матрица. Достаточное условие существования обратной матрицы.

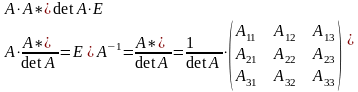
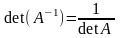
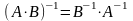
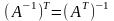
Для того чтобы матрица имела обратную достаточно того, чтобы она была невырождена.

Основные действия над матрицами

Сумма (разность) матриц.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера.

Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

c_ij = a_ij  b_ij

Обозначение: С = А + В = В + А.

Умножение матрицы на число.

Операция умножения матрицы любого размера на произвольное число сводится к умножению каждого элемента матрицы на это число.

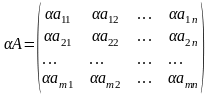
Свойства: (АВ) =А  В

А() = А  А

Пример: Даны матрицы А = Произведение двух матриц.

Замечание: Операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй. В противном случае произведение матриц не определено.

Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:Обозначение: AB = C;

Из приведенного определения видно, что каждый элемент матрицы С равен алгебраической сумме произведений элементов i – той строки матрицы А на соответствующие элементы j – го столбца матрицы В.Свойства:

1) Умножение матриц не коммутативно, т.е. АВ  ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

Транспонирование матриц

Определение. Матрицу А^Т называют транспонированной матрицей А, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы А^Т.(т.е. строки матрицы А заменены на столбцы и наоборот)

А = 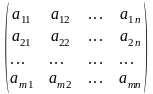; А^Т= ;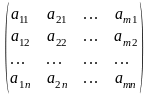

Векторы Вектор - это направленный прямолинейный отрезок, т.е. отрезок, имеющий длину и определенное направление. Свойства линейных операций:

1)      ;

2)      ;

3)      ;  ;

4)      ;

5)      ;

6)      ;

7)      ;  ;

Сложение векторов. Пусть   и   – два произвольных вектора. Возьмем произвольную точку О и построим вектор  ; затем от точки А отложим вектор  . Вектор  , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается   (рис. 1).

 

 

Рис. 1

Ту же сумму можно получить иным способом. Отложим от точки О векторы   и  . Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор   – диагональ параллелограмма – является суммой векторов   и   (рис. 2).

 

Рис. 2

Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).

 

Рис. 3

Вычитание векторов. Разностью   векторов   и   называется такой вектор  , который в сумме с вектором   дает вектор  :     .

Если векторы   и   привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).

 

Таким образом, если на векторах   и  , отложенных из общей точки О, построить параллелограмм ОАСВ, то вектор  , совпадающий с одной диагональю, равен сумме  , а вектор  , совпадающий с другой диагональю, – разности   (рис. 5).

 

Умножение вектора на число. Произведением вектора   на действительное число   называется вектор   (обозначают  ), определяемый следующими условиями:

1)      ,

2)       при   и   при  .

Очевидно, что при    .

Построим, например, векторы   и   для заданного вектора   (рис. 6).

Рис. 6

Из определения следует: два вектора   и   коллинеарны тогда и только тогда, когда имеет место равенство  :

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору. Для коллинеарности вектора   ненулевому вектору   необходимо и достаточно, чтобы существовало такое число λ, что

векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.

Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны

Для компланарности трех векторов   и   трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Условия ортогональности векторов. Два вектора 

a

 и 

b

 ортогональны (перпендикулярны), если их скалярное произведение равно нулю

a Угол между векторами 

      Векторным произведением вектора 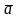на вектор 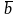называется вектор , который:

Перпендикулярен векторам и .

Имеет длину, численно равную площади параллелограмма, образованного на векторах и .

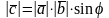, где

Векторы , и образуют правую тройку векторов.Свойства: