Ачх замкнутой сар по возмущающему воздействию

;

;

И-регулятор:

m₁=0.25; K₀=0.272; K_у=2;

m₁=0.35; K₀=0.21; K_у=2;

П-регулятор:

m₁=0.25; K₁=8; K_у=2;

m₂=0.35; K₁=4; K_у=2;

ПИ-регулятор:

m₁=0.25, k_У=2; k₀=1,8; k₁=3,7;

m₁=0.35, k_У=2; k₀=0,96; k₁=1,96;

АЧХ правее точки ПИ-регулятора:

m₁=0.25, k_У=2; k₀=1,72; k₁=4,165;

m₁=0.35, k_У=2; k₀=0,6; k₁=3,2;

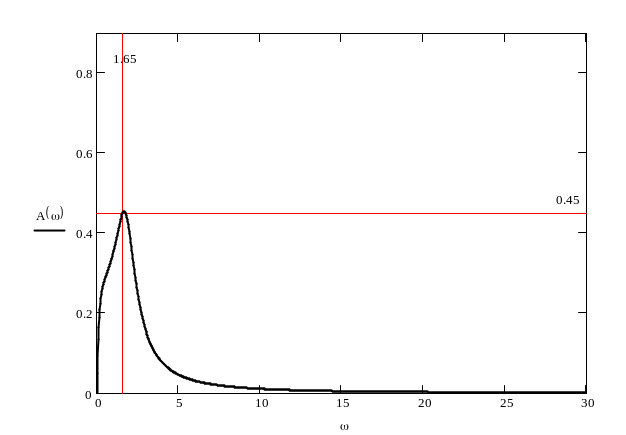
Качественные показатели ачх

Регулятор		Параметры
		ωр		М
И	m1	0.48	3.1
	m2	0.42	2.6
П	m1	2.76	0.55
	m2	1.89	0.65
ПИ	m1	1.86	0.55
	m2	1,29	0.74
Пр	m1	1.98	0.48
	m2	1.65	0.45

Показатель колебательности

И-регулятор М=А(w_р)-0.3

П-регулятор М=А(w_р)+0.3

ПИ-регулятор М=А(w_р)

Часть 2: Интегральные квадратичные критерии. Оценка качества переходных процессов сау по интегральным квадратичным критериям.

Цель работы: оценка качества переходных процессов САУ по интегральным квадратичным критериям.

Структурная схема системы

x y

Дано:

Т₁=0,4; Т₂=0,9.

Передаточная функция разомкнутой системы:

Передаточная функция замкнутой САУ:

Вычислим критический коэффициент усиления к_кр по критерию Рауса-Гурвица.

Характеристическое уравнение:

Условие границы устойчивости:

Вычисление интегральных критериев i0 и i1.

Найдем выражение интегрального квадратичного критерия при .

Изображение ошибки регулирования:

Установившаяся ошибка :

Изображение переходной составляющей ошибки регулирования:

т.к

Это выражение соответствует виду :

Из полученного результата следует, что I₀ уменьшается с ростом коэффициента усиления разомкнутой системы k.

Найдем выражение для :

Это выражение соответствует виду для :

Условие оптимальности значения :

Коэффициент веса:

Как видно из полученного результата, увеличение γ приводит к уменьшению коэффициента усиления и, следовательно, к менее колебательному переходному процессу.

Определение параметров для различных коэффициентов веса

Для значений γ = 0; γ = 1; γ = 3; γ = 5 определим численные значения коэффициента усиления регулятора k_опт, интегральные критерии I₀, I₁₀ и I_1min, а также значение . Изобразим графики эталонных кривых y(t) для расчетных значений γ и области допустимых значений переходного процесса.

Расчетные значения параметров К_опт, I₀, I₁₀, I_1min, I^*_1min, Δ=(δ/γ)^1/2

при γ = 0, γ = 1, γ = 3, γ = 5.

Параметры	Расчетные значения параметров
	γ = 0	γ = 1	γ = 3	γ = 5
Копт	1,14	0,69	0,3	0,188
I0	3471	3820	5939	8363
I10	2082	1066	409	248
I1min	3471	4886	9620	14563
I*1min	0	2500	7500	12500
Δ=(δ/γ)1/2		48,8	26,6	20,3

Зависимость показателей качества ПП от изменения коэффициента веса.

Расчетный параметр	Прямые показатели качества
	Время переходного процесса, tп. п.	Перерегулирование, σ %	Колебательность, К
γ=0	11,2	38,44	2
γ=1	6,8	19,6	1
γ=3	6,7	0 монотонность	0
γ=5	12,8	0 монотонность	0