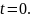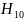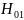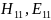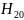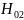27)Условия распросранения эвм в прямоугольном волноводе

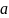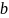1. Индексы и указывают на число стоячих полуволн, укладывающихся вдоль размеров и соответственно. Решение для составляющих электромагнитного поля, соответствующее определённым целым значениям пары чисел и , называются парциальными волнами и обозначаются - или 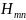-волнами.

2. В прямоугольном волноводе не может распространяться волна типа 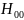, так как поперечные составляющие , обращаются в ноль ).

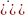3. В прямоугольном волноводе не могут существовать волны типа и 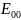, так как в этом случае вектор-потенциал равен нулю и составляющие поля пропадают.

4. Любой парциальной волне соответствует вполне определённая постоянная распространения:

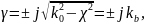
где 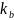– волновое число волновода для данного типа волны.

Для того чтобы волна распространялась, необходимо, чтобы было действительным числом:

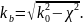
При этом должно выполняться условие:

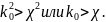
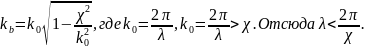
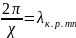
Величина 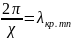нызывается критической длиной волны в волноводе:

(4.34)

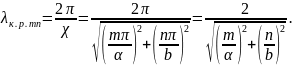X

Замечаем, что если , то распространение волны в волноводе возможно. Если 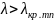, то соответствующая волна не будет распространяться в волноводе, так как будет чисто вещественным числом, а это соответствует тому, что волна будет затухать по экспоненциальному закону от места её возникновения.

Волны, для которых , называются местными. При строгом решении задачи данные волны необходимо учитывать, особенно в местах неоднородностей и в месте возбуждения колебаний. Можем записать:

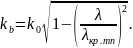
Найдём длину волны в волноводе, т. е. ,

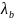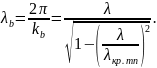
(4.35)

Из (4.35) следует, что длина волны в волноводе не равна длине волны в свободном пространстве:

5. Характеристическое сопротивление для -волны

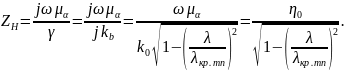
(4.36)

где 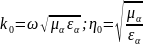– волновое сопротивление среды, заполняющей внутреннюю полость волновода.

Видим, что .

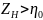Характеристическое сопротивление для -волны

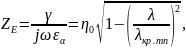
т. е. 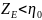. Замечаем, что

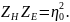
Характеристические сопротивления 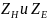в литературе называют волновым сопротивлением по полю.

Таким образом, в прямоугольном волноводе могут распространяться волны:

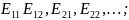
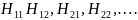
Данные волны могут существовать и распространяться в волноводе, причём совместно, если выполняется условие 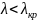для этих волн.

На практике стремятся, чтобы электромагнитная энергия передавалась на одной волне. Для этого необходимо, чтобы для данной волны выполнялось условие 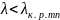, а для остальных волн должно выполняться условие . В таблице приведены значения 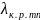, рассчитанные в соответствии с формулой (4.34) .

Тип волны
	2a	2b		a	b

Из приведённой таблицы следует, что для существования в волноводе одной волны, например , должны быть выполнены условия:

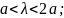
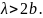
Если же 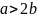, что практически выполняется, то условие существования волны будет одно;

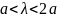при 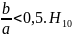-волна имеет наибольшую критическую длину волны, поэтому она называется основной волной прямоугольного волновода.

Кроме этой особенности, волна обладает рядом других преимуществ по сравнению с другими типами волн:

имеет наиболее простую структуру поля и наиболее легко возбуждается в волноводе;

с помощью волны при данном поперечном сечении волновода можно передать максимальную мощность;

затухание мощности на единицу длины волновода меньше, чем для других волн.

В силу этих особенностей волна нашла наиболее широкое распространение в технике СВЧ.

Запишем составляющие воля волны . Для этого в выражениях (4.28 – 4.29) и (4.31 – 4.32) для

-волны положим 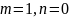. Получим:

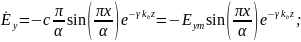
(4.37)

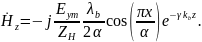
(4.38)

Из (4.38) следует, что волна имеет только три компоненты .

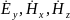Рис. 4.11

Для мгновенных значений составляющих вектора поля получим:

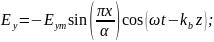
(4.39)

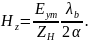
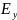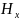Формулы (4.39) показывают, что и изменяются в противофазе друг с другом, а составляющая сдвинута по фазе относительно и на четверть периода, причём в сторону отставания по отношению к . На рис. 4.11 приведены картины силовых линий поля волны в различных сечениях волновода при