Вопрос 9.

1.10. Волновые уравнения для векторов

Рассмотрим волновые уравнения для случая однородной, изотропной среды. Даны уравнения Максвелла:

(1.57)

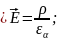
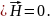
Задача заключается в решении уравнений Максвелла. Преобразуем уравнения (1.57) таким образом, чтобы получить отдельно уравнение для и отдельно уравнение для [1,6]. Для этого возьмём от первого уравнения и, используя второе уравнение, получим:

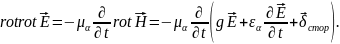
Учитывая, что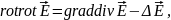 соберём все члены, содержащие в левую часть, получим:

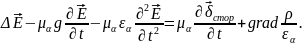(1.58)

Аналогично для . Возьмём от второго уравнения и, используя первое, получим:

(1.59)

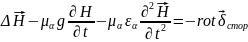
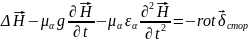
Уравнение (1.58) есть волновое уравнение для вектора , а (1.59) – волновое уравнение для вектора .

Правые части уравнений (1.58) и (1.59), которые выражаются через заданные функции и , достаточно сложны. Непосредственное решение уравнений (1.58) и (1.59) встречает большие трудности. Для того чтобы облегчить решение этих уравнений, вводятся вспомогательный вектор и функция, так называемые электродинамические потенциалы. При этом уменьшается число уравнений, правая часть их упрощается. После определения вспомогательных функций и определения через них и , не нужно устанавливать соответствие между ними.

Вспомогательными функциями бывают вектор-потенциал и скалярный потенциал, а также вектор Герца.

Вопрос 10.

1.12. Переменное электромагнитное поле. Запаздывающие потенциалы

Переменное электромагнитное поле характеризуется известными нам тремя уравнениями (1.66 – 1.68). В случае переменного электромагнитного поля нет возможности разделить магнитное поле от электрического. Это процесс взаимосвязанный. При решении необходимо знать либо сторонние токи, либо сторонние заряды, начальные и граничные условия.

Если имеем однородное безграничное пространство, то нам нужно знать только токи и заряды. На практике этот случай редок, но он имеет фундаментальное значение.

Рассмотрим этот случай для среды без потерь, т. е. при уравнения (1.66 – 1.68) примут вид:

(1.70)

;

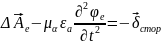
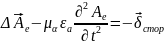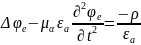
(1.71)

;

^.

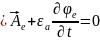Уравнение (1.70) может быть записано в виде трёх скалярных уравнений в прямоугольной системе координат. В результате имеем:

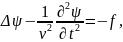
(1.72)

где – проекции или функции ;

– означает 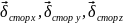или ;

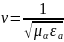– имеет размерность скорости.

Рис. 1.13

Уравнение (1.72) есть неоднородное волновое уравнение. Частным решением его является

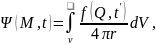
(1.73)

где – объём области пространства, в котором задана функция (рис. 1.13);

– точка, находящаяся в объёме , в ней расположен источник поля;

– время, предшествующее времени на величину ;

– время запаздывания, которое необходимо, чтобы процесс распространялся от точки до точки .

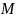Данный потенциал определяется поведением источников в момент времени . Потенциалы в силу наличия времени запаздывания называются запаздывающими. В результате для электрического вектор-потенциала и скалярного потенциала получим:

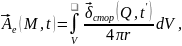
(1.74)

(1.75)

Формулы (1.74) и (1.75) находят широкое применение для расчёта изучения антенн, когда токи в них заданы.