Вопрос 1.
1.5. Закон электромагнитной индукции и его обобщение
Согласно закону Фарадея в замкнутом проводнике, помещённом в магнитное поле, возникает ЭДС, пропорциональна скорости изменения магнитного потока, пронизывающего этот контур,
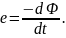
(1.26)
Обобщим
этот закон, чтобы найти соотношение
между
и
в
точке пространства.
Учитывая,
что ЭДС в замкнутом контуре
,
а магнитный поток, пронизывающий площадь
,
ограниченную контуром
,
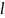получим
из (1.26):
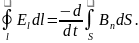
(1.27)
Наличие проводника позволяет лишь зафиксировать (обнаружить) ЭДС Таким образом, если имеем в пространстве переменное магнитное поле, то возникает и электрическое поле и они связаны соотношением
Интегрирование здесь ведётся по воображаемому контуру. Если будем рассматривать неподвижные среды, где магнитное поле меняется во времени, а контур фиксирован, то (1.27) можно переписать в виде:
(1.28)
При условии непрерывности подынтегральных функций и, сделав предельный переход, аналогично, как в выражении (1.18) получим
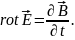
(1.29)
Это
дифференциальная форма закона
электромагнитной индукции, связывающая
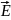и
,
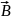в точке пространства. Подчеркнём, что
из обобщений Максвелла вытекает
исключительно важное представление о
физической природе поля.
Существование электрического поля связано не только с наличием электрических зарядов, но для его возникновения также достаточно только изменения во времени магнитного поля.
Из (1.29) находим, что
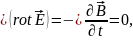
так
как
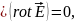т.
е.
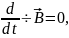поэтому всегда
Перестановка оператора
и
допустима, так как по предложению в
обыкновенной точке поля вектор
непрерывен со всеми своими производными.
Из
постоянства дивергенции в любой точке
поля следует, что если когда-либо в
прошлом поле отсутствовало (т. е. было
время, когда
),
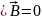то и всегда
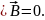Утверждение о том, что всегда
находится
в соответствии со сделанным ранее
указанием на соленоидальность поля
вектора
,
вследствие отсутствия истинного
магнетизма (магнитных масс).
Вопрос 2.
1.3. Вектор напряжённости электрического поля и вектор электрической индукции
Между
электрическими зарядами имеется
взаимодействие. Впервые это взаимодействие
было обнаружено Кулоном. Если имеем 2
точечных заряда
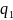и
,
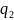то сила взаимодействия между зарядами
определяется выражением
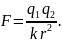
(1.12)
Выражение
(1.12) есть закон Кулона, где
– коэффициент, зависящий от свойств
среды и выбора систем единиц. Данное
взаимодействием обусловлено взаимодействие
электрических полей данных зарядов.
Поле заряда определяется его напряжённостью , которая равна той силе, которую испытывает единичный точечный заряд, помещённый в данную точку поля:
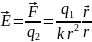
(1.13)
,г
де
– единичный вектор, который вводится
для определения направления вектора
.
Рис. 1.4
Значение зависит от свойств среды (коэффициент ). Это затруднение можно устранить путём введения дополнительного вектора – вектора электрической индукции или вектора смещения – . Этот вектор был введён Максвеллом путём высказанного им постулата: поток вектора через любую замкнутую поверхность (см. рис. 1.3) при любом распределении заряда внутри этой поверхности и независимо от свойств среды равен количеству электричества (заряду), находящемуся внутри этой поверхности:
(1.14)
Выражение (1.14) представляет постулат Максвелла.
Если
заряд распределён внутри объёма
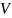с объёмной плотностью
,
то
Поэтому
(1.14) можно записать в виде
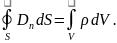(1.15)
Формула (1.15) есть интегральная форма постулата Максвелла.
Если под интегральные функции в объёме и на ограничивающей его поверхности непрерывны, то, применив к (1.15) формулу Остроградского, (1.11) получим:
Следовательно,
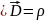
(1.16)
.Это
дифференциальная форма постулата
Максвелла. Она показывает, что заряды,
распределённые с объёмной плотностью
являются источником вектора
.
Отсюда видим, что
не зависит от свойств среды.
Поле
вектора
удобно представить в виде линий вектора
,
в каждой точке которых вектор
совпадает по направлению с касательной
к этой линии (рис. 1.5),
непосредственно в месте расположения
заряда. Вне заряда
так
Рис. 1.5
Таким образом, при наличии электрических зарядов, линии вектора должны быть разомкнуты, начинаясь на положительном заряде и кончаясь на отрицательном.