32. Сигналдарды спектральды талдау. Спектральды талдаудың кейбір мәселелері. Фурьенің тура және кері түрлендіруін қолданыңыз. Тез Фурье түрлендіруі

ДФТ-дің бір коэффициетін (28)-формуламен есептеу үшін N комплексті көбейту мен қосуды орындау қажет. Сондықтан, N коэффициентті барлық ДФТ-дің есептеуі N² «көбейту-қосу» операциялар жұбынан тұрады. Операциялардың саны ДФТ-дің өлшемінің квадратына пропорционал өседі. Бірақ, егер N қарапайым сан болмаса және көбейткіштерге жіктелсе, талқыланатын санаулар жиынтығын бөлшектерге бөліп, олардың ДФТ-ін есептеп және нәтижелерін біріктіріп, есептеу процесін тездетуге болады. Мұндай есептеу тәсілдерін тез Фурье түрлендіруі (ТФТ) деп аталады және практикада жие қолданады.

Қазіргі кезде ТФТ алгоритімін жүзеге асыратын процедуралар жоғары деңгейлі программалау тілдерінде программа жазу үшін қолданатын барлық математикалық кітапханаларға және математикалық есептеулердің арнайы жүйелеріне (MatLab, MathCAD, MapleV, Mathematica және т.б.) кіреді. MatLab жүйесінде тез Фурье түрлендіруі тура және кері ТФТ-ін орындайтын функциялар жұбынынан іске асырылады: fft/ifft. Бұл функциялар нақты да, комплексті тізбектерге де қолданылады, тізбектердің ұзындығы кезкелген болу мүмкін.

fft(ν) – 2^m-өлшемді вектордың дискретті Фурье түрлендіруі, аргументі функцияның уақыт бойынша бірдей арақашықтық дискреттеу нәтижесі болып табылады. Программаның жұмыс істеу нәтижесі – 2^m+1-мөлшерлі комплексті вектор. fft функциясының кері векторының элементтері

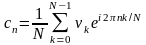
формуласымен есептеледі, мұнда N – νвекторының элементтер саны.

ifft(ν) – ДФТ мәндеріне ие комплексті вектордың кері дискретті Фурье түрлендіруі. ν векторы 2^m+1 элементтерден тұру керек. Программаның жұмыс істеу нәтижесі – 2^m+1-мөлшерлі нақты вектор. Вектордың элементтері

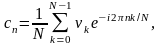
формуласымен есептеледі, мұнда N – νвекторының элементтер саны. Барлық векторлар үшін ifft(fft(ν))=ν қатынасы дұрыс.

fft(ν,n) – 2ⁿ-өлшемді вектордың дискретті Фурье түрлендіруі, бірсыпыра функцияның уақыт бойынша бірдей арақашықтық дискреттеу нәтижесі аргументі болып табылады. Программаның жұмыс істеу нәтижесі – 2ⁿ⁺¹-мөлшерлі комплексті вектор. Егер n > length(ν) болса, ν векторындағы тізбек нольдермен толтырылады.

ifft(ν,n) – ДФТ мәндеріне ие комплексті вектордың кері дискретті Фурье түрлендіруі. Программаның жұмыс істеу нәтижесі – 2ⁿ⁺¹-мөлшерлі нақты вектор.

33. Периодты және периодты емес сигналдарды өндіруге арналған MatLab жүйесіндегі функцияларды көрсетіңіз.Периодты: Square- тікбұрышты импульстер тізбегі;

Fs=1e3;

t=-10e-3:1/Fs:50e-3;

A=3; f0=50; tau=5e-3;

s=(square(2*pi*t*f0,f0*tau*100)+1)*A/2;

plot(t,s,'k');

ylim([0 3.5]); title('square').

Sawtooth-үшбұрышты:

Fs=1e3;

T=-25e-3:1/Fs:125e-3;

A=5;

T=50e-3;

t1=5e-3;

s=(sawtooth(2*pi*t/T, 1-t1/T)-1)*A/2;

plot(t,s,'k'); title('sawtooth').

Diric-Дирихле ф/ясы(периодты sinc ф/ясы):

x=0:0.01:15;

subplot(2,1,1);

plot(x,diric(x,7),'k');

title('diric.n=7');

subplot(2,1,2);

plot(x,diric(x,8),'k');

title('diric.n=8');

Периодсыз:

Tripuls-ушбурышты:

Fs=1e3;

t=-50e-3:1/Fs:50e-3;

A=10; T1=20e-3; T2=60e-3;

s=A*(T2*tripuls(t,T2)-T1*tripuls(t,T1))/(T2-T1);

plot(t,s,'k');

title('tripuls');

sinc-шогыр импульс:

Fs=1e3;

t=-.1:1/Fs:.1;

f0=10;

f=-50:50;

T=1/f0;

s=rectpuls(t,T).*cos(2*pi*f0*t);

sa=T/2*(sinc((f-f0)*T)+sinc((f+f0)*T));

subplot(2,1,1);

plot(t,s,'k');

title('Radio Impulse');

subplot(2,1,2);

plot(f,abs(sa),'k');

title('sinc')

rectpuls-ткбурышты:

Fs=1e3;

t=-40e-3:1/Fs:40e-3;

A=5;

T=20e-3;

s=-A*rectpuls(t+T/2,T)+A*rectpuls(t-T/2,T);

plot(t,s,'k').

Дискретты:

t=0:0.001:2;

x=sin(2*pi*5*t)+cos(2*pi*12*t);

plot(t,x); grid

set(gca, 'FontName', 'Arial Cyr', 'FontSize',16);

title('Ainurkin'); xlabel('c'); ylabel('x(t)');

y=fft(x):

a=abs(y); figure(2), plot(a); grid

set(gca, 'FontName','Arial Cyr','FontSize',16);

title('Fureou'); xlabel('vector nomeri'); ylabel('nnn')

z=ifft(y):

figure(3), plot(t,z); grid

set(gca,'FontName','Arial Cyr','FontSize',16);

title('keri Fureou'); xlabel('ccc'); ylabel('z(t)')