30. Автотербелмелі жүйе – Ван-дер-Поль генераторы.

Динамикалық жүйенің тербелмелі процестерін зерттегенге қажет болғаны соншалық, А.А.Андронов бұл типке арнайы термин – автотербелмелі жүйе деген ұғым енгізді.

Динамикалық жүйедегі автотербеліс периодты ғана емес, квазипериодты және стохасты та болуы мүмкін. Сондықтан біз тек ең жалпы анықтамасын береміз. Автотербелістер – бұлар бастапқы шартқа тәуелді емес өшпейтін тербелістер, түрі және қасиеті осы бейсызық диссипативті жүйенің өзімен сипатталады және жүйе сыртқы энергия көзімен қуаттандырылады. Автотербелістер диссипативті жүйелердегі басқа тербелістерден негізінде мүлдем ерекше, оларды үзбеу үшін сырттан периодты әсер қажет емес.

Динамикалық жүйенің мысалы ретінде классикалық бейсызық Ван-дер-Поль осцилляторын қарастырамыз. 4-суретте Ван-дер-Поль генераторының принциптік сүлбесі келтірілген.

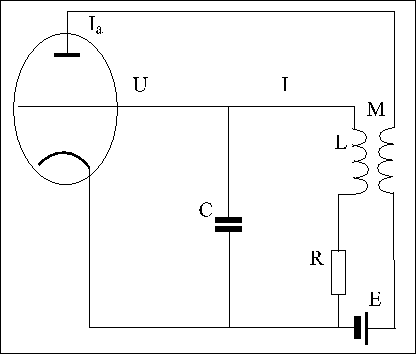
Біз Ван-дер-Поль теңдеуін сандық модельдеуге ыңғайлы мына түрде қарастырамыз: .

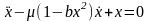М-файлда мынадай листинг курайык:

function dydt=vanderpoldemo(t,y,a,Mu)

dydt=[y(2); Mu*(a-y(1)^2)*y(2)-y(1)];

Ал жұмыс ортасында мынайдай программа жазамыз:

tspan=[0,100]; x0=[0.5;0]; a=10.0; Mu=10.0;

disp(['Fig0 tspan=[0,100]; mu=', num2str(Mu)])

tic

[t,x]=ode45(@vanderpoldemo,tspan,x0,[],a,Mu);

toc

plot(t,x(:,1),'b','LineWidth',4)

xlabel('t'); ylabel('solution x')

title(['van der pol eqation,\mu=',num2str(Mu)])

hold on; tic

[t,x]=ode15s(@vanderpoldemo,tspan,x0,[],a,Mu);

toc;

plot(t,x(:,1),'r--','LineWidth',4); hold off

Сыртқы гармониялық ұйытқуды ескергендегі (амплитудасы ) және кері байланыс коэффициенті (теріс кедергі) , бейсызық тербелістер жиілігі 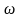болатын Ван-дер-Поль теңдеуі мына түрде жазылады:

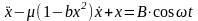. (18)

31. Fminbnb функциясы. Көпөлшемді шартсыз минимизациялауды көрсетіңіз. Шарт қою арқылы минимизациялауды көрсетіңіз.

Бір айнымалы функцияның минимумын табу үшін алтын қиық әдісі немесе параболалық интерполяция әдісі қолданылады және Fminbnd программасының көмегімен жүзеге асырылады.

Мысалы: f(x)=24-2x/3+x²/30 [5; 20]

>>x=5.0:0.001:20.0; y=24-2*x/3+x.^2/30;

>>plot(x,y);grid on

>>[x,y]=fminbnd(‘(24.0-2*x/3+x.^2/30)’,5.0,20.0)

X= 10.0000

Y= 20.667

Көпөлшемді шартсыз минизациялау

Fminsearch функциясында симплекстік іздеу алгоритмі қолданыладыб оның идеясы келесіде:n-өлшемді кеңістіктің бастапқы нүктесінің маңайында (n+1) - симплексті тұрғызылады, жалпы жағдайда. Осы нүктелерде мақсат функциясының мәндері есептеліп, функцияның мәні максималы болатын нүкте қарастырылудан алынып тасталады, ал оның орнына ережелерге сай симплекске басқа нүкте қойылып отырады. Симплекс диаметрі берілген аралықтан кіші болған жағдайда үрдіс тоқтатылады. Мақсат функциясы тегіс емес тіпті үзілісті болуы мүмкін.

Бұл функцияға қатысудың ең қарапайым түрі келесідей:

X=fminsearch(fun,x0)

Екі айнымалыдан тұратын үзілісті, бірақ тегіс емес функцияның мысалын қарастырайық у=fun(x)=3|x₁|+|x₂| оның жалғыз минимумы координаталар жүйесінің бастапқы нүктесінде орналасқан.

>>[x,f]=fminsearch(‘3*abs(x(1))+abs(x(2))’,[1;1])

>>x= 1.0e-004*

-0,1439

0.3565

F= 7.8809e-005

Шартсыз минимизациялау.

Егер нақты функцияның аргументіне теңдеулер немесе теңсіздіктер түріндегі қандай да бір шектеулер қойылса, онда y=f(x) векторлық аргументтен тәуелді нақты функцияның минимумын іздеу есебі шартты деп аталады. Ондай есептерді шешу Лагранждың көбейткіштерін қолдану әдісіне негізделген. Әрбір g(x)≤0 теңсіздігі g(x)+v²=0 теңдеуімен алмастырылады. Одан кейін әрбір тңдеудің сол бөлігі қандай да бір көбейткішпен мақсат функциясына қосылады, ол көбейткіштер және v шамалары айнымалылар қатарына қосылады. Осы түрде модификацияланған функция үшін шартты минимизациялау есебі шешіледі. Шартсыз минимизациялауда fmincon қолданылады.

Жартыжазықтықтағы Розенброк функциясының минимумы

Жартыжазықтықты беретін және x₁-x₂+4≤0 шектеулерін ескере отырып Розенброк функциясының минимумын табайық. A=[1 -1] Матрицасын , b=[-4] Векторын, x0 бастапқы нүктесін анықтаймыз, x0=[-3; 4] және fmincon функциясын шақырамыз:

>> A=[1 -1]; >> b=[-4]; >> x0=[-3; 4];

>>x=fmincon(‘5*(x(2)-x(1)^2)^2+(1-x(1))^2’,x0,A,b)

X= 2.5431

6.5431

[x,fval]=fmincon(….) Түріндегі толық шақыру барысында мақсаттық функцияның берілген нүктедегі мәнін табуға болады:

Fval= 2.4098