27. Бар блоктарды топтастыру арқылы бағыныңқы жүйелерді құрыңыз

Егер модельдердің блок-үрдісі өте күрделі және үлкен болса, онда блоктарды бағыныңқы жүйеге топтастыру арқылы жеңілдетуге болады. Бағыныңқа жүйелерді қолдану келесі мүмкіндіктерді береді:

• Модель терезесінде шығатын блок көлемі қысқартылады

• Функционалды байланысқан блоктрады бір топқа біріктіруге мүмкіндік туады

• Тармақтық блок-үрділерінің құрылуына мүмкіндік туады.

Бағыныңқы жүйені екі әдіспен құруға болады:

1. Subsystem блогын модельге қосып, содан кейін бұл блокқа кіріп, пайда болған бағыныңқы жүйе терезесіне келесі бағыныңқы жүйені құру

2. Модельдің блок-үрділерінің бөлігін ерекшелеп, бір бағыныңқы жүйеге біріктіру.

Бар блоктарды топтастыру арқылы бағыныңқы жүйелерді құру

Егер блок-үрді құрамында бағыныңқы жүйеге біріктіретін блоктар бар болса, онда соңғысын мына түрде құруға болады:

1. Бағыныңқы жүйе құрамына енгізу керек болатын блоктарды және оларды біріктіретін сызықтарды жиек арқылы ерекшелейді.

2. Edit мәзірінен Create Subsystem командасын таңдалады. Нәтижесінде Simulink ерекшеленген блоктарды Subsystem блогымен ауыстырады. Құрылған бағыныңқы жүйенің блок-үрдісін көру үшін Subsystem блогын екі рет басу керек.

28. Тиімділеу әдістерін сандық шешіңіз

Мүмкін болатын барлық жағдайдың ішінен ең жақсысын таңдауды тиімділеу деп түсінеміз. Тиімділеу есептерін шешу барысында кейбір параметрлердің оңтайлы мәндерін табу қажет. Тиімді шешімді таңдау мақсат функциясы деп аталатын функцияның көмегімен жүзеге асады. Мақсат функцияны келесі түрде жазуға болады: 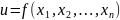, мұндағы 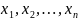– параметрлер.

Тиімділеу есептерінің екі түрге бөліп қарастаруға болады – шартты және шартсыз. Шартсыз тиімділеу есебінің мәні n нақты айнымалыдан тұратын функцияның максимумын немесе минимумын табуға және n-өлшемді кеңістіктің қандай да бір G жиынында аргументтердің сәйкес мәндерін анықтауға тіреледі. Көбінесе минимизациялау есептері қарастырылады; мақсат функциясының таңбасын қарама-қарсыға ауыстыра отырып, максимумды іздеу есептеріне жеңіл көшуге болады. Шартты тиімділеу есептері дегеніміз – оларды құру барысында G жиынында қандай да бір шарттар (шектеулер) қойылады. Матлаб ортасында шартсыз минимизациялау есебінің шешімдерін табудың әртүрлі мүмкіндіктерін қамтамасыз ететін бірнеше функцияны қарастыруға болады.

29. Бір белгісізді теңдеудің түбірін табу. Бейсызық теңдеулер жүйесін шешу

Fun(x)=0 түріндегі теңдеуді шешу үшін fzero функциясы қолданылады. Түбірі ізделініп отырған функцияны шақырудың ең қарапайым жағдайында оған сілтеуішті қолданады, сонымен қатар түбір ізделінетін аймақтың бастапқы нүктесі x0 беріледі: x=fzero(f, x0).

Мұндағы f аргументі төмендегілердің біреуі арқылы берілуі мүмкін:

• Апостроф белгісіне алынған х-белгісізден құрылған формула

• M-файлдың аты түрінде

• Функцияға сілтеуіш ретінде

• Аты белгісіз функцияға сілтеуіш түрінде

х0 агументі келесі екі мүмкіндіктің біреуі арқылы беріледі:

• [a, b] вектор (a<b) интервалында анықталған [a, b] векторы түрінде және f функциясы интервалдың шекті нүктелерінде таңбасын өзгертеді, мұның өзі осы интервалда ең болмағанда бір түбірдің табылатындығының айғағы;

• Аймағында түбірдің табылуы мүмкін болып есептелетін скалярлы мән. Бұл жағдайда fzero функциясы центрі берілген x0 нүктесі болатын және шекті нүктелерінде f функциясы таңбасын өзгертетін интервалды өзі табуға тырысады.

Бастапқы жуықтауды таңдауды жеңілдету үшін y=fun(x) функциясының графигін тұрғызуға болады.

Бейсызық теңдеулер жүйесін шешу

fsolve функциясы F(x)=0 түріндегі сызықтық емес теңдеулер жүйесін шешуге арналған, мұндағы х-белгісіздер векторы немесе матрица, ал F – мәні вектор немесе матрица болатын функция. Бұл функцияның орындалу алгоритмі х0 бастапқы мәнін пайдалана отырып F функциясының құраушыларының квадраттарының қосындысын Гаусс-Ньютон және Левенберг-Марквард әдістерімен минимизациялауға негізделген. Қарапайым жағдайда fsolve функциясы келесі түрде шақырылады: х=fsolve(F, x0)

fsolve функциясының екінші аргументі вектордың бастапқы мәндері түрінде берілуі мүмкін және вектордың әрбір компоненті үшін жақын жатқан шешім табылады: x=fsolve(@sin, [1 2 3 4 5 6], optimset(‘fsolve’))

Барлық тиімділеу және сызықтық емес теңдеулер жүйесін шешу функцияларының кіріс параметрлерінің қасиеттерін итерациялық үрдістердің орындалуына әсер етеді. Ол қасиеттер өрістері optimset функциясының көмегімен құрылатын options құрылымы арқылы құрылады.