25. Function and Tables кітапханаларын артықшылығын көрсетіңіз. Nonlinear кітапханасы.Signals and Systems кітапханасы.
Function & Tables кітапханасы
Берілген кітапхана құрамына математикалық функциялар кітапханасында жоқ функциялармен жұмыс істеуге, сонымен қатар кестелік функциялармен жұмыс істеуге мүмкіндік беретін блоктар енеді. Оған Fcn, Matlab Fcn (Matlab пакетінің функциялары), S-Function (S функция) ж\е т.б. жатады.
Fcn блогы – бұл әмбебап “есептеуші” блок. Құру парметрі ретінде әрбір есептеуіш мәнді енгізуге болады, оның аргументі кіріс сигналының мәні болады.
Кіріс сигналы белгілеу үшін u символы қолданылады. Егер кіріс сигналы вектор болып келсе, онда оның жеке элементтері үшін жүргізілетін операцияларға аргумент міндетті түрде берілу керек. Мысалы, екі кіріс сигналының қосындысы мына түрде жазылу керек: u(1)+u(2)
Nonlinear кітапханасы
Бұл кітапхананың құрамында сызықтық емес функциялармен жұмыс істейтін блоктар бар. “Қайта қосу блоктар” жеке топ құрады, яғни сигналды жіберу
бағытын басқарушы блоктар. Ондай блоктар төртеу:
Switch (қайта қосушы құрал)
Manual switch (қолдан қосатын құрал)
Multiport switch (көп кірісті қайта қосқыш)
Reley(реле)
Switch блогының үш кірсі бар: екі ақпараттық (1 және 3) және бір басқарушы.
Signals & Systems кітапханасы
Құрылымы бойынша Signals & Systems бөлімі – ең үлкен және Simulink
кітапханаларының имитациялық модельдеу бөлімінің тиімдісі. Оның құрамында отыз блоктар бар. Оның ішінде жиі қолданылатындары мыналар:
In (кіріс порты) және Out (шығыс порты) - модельдің бағыныңқы жүйелері аралығы мәлеметтермен алмасуды қамтамасыз етеді, сонымен қатар Matlab жұмыс аймағы мен модель арасында жүреді.
Bus Selector (шина селекторы) – сигналдар тобының ішінен бір берілген сигналды ерекшелейді.
Mux (араластырғыш) - кіріс сигналдарын бір векторлық сигналға біріктіреді.
Demux (бөлгіш) –Mux блогының функцияларына қарама қарсы функцияларды іске асырады.
Subsystems – бағыныңқы жүйелерді құрайтын блок.
Mux блогы кіріс шамаларын бір сызықтық векторға біріктіреді.
Мұндағыкіріс шамалары скалярлық та, векторлық та бола алады. Нәтижедегі вектордың өлшемі кірс портына түсетін элементтердің барлық сандарының қосындысына тең.
26. Бейсызық маятниктің фазалық портретін алыңыз
Маятниктің аз ауытқу қозғалысы белгілі – бұл гармониялық тербелістер. Маятниктің қозғалыс заңы келесі түрде жазылады:
,
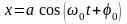(1)
мұнда
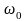– тербелістің жиілігі, а – амплитуда,
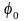– бастапқы фаза. Егер ауытқулар аз
болмаса, тербелістерді сипаттайтын
теңдеу
.
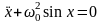(2)
(2)-теңдеу
бейсызық, оның шешімі, басқа көп бейсызық
теңдеулердің шешімдері сияқты, элементар
функциялармен жазылмайды, сондықтан
оның сандық шешімін алу қажет. Мейлінше
аз ауытқу бұрышы кезінде (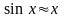
,
мұнда х-пен маятниктің ауытқу бұрышы
белгіленген) теңдеу сызықты болады
,
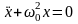оның шешімі (1)-түрде жазылады.
Маятниктің
қозғалысының зерттеу нәтижелерін
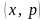жазықтықта қисықтар жиыны ретінде салу
ыңғайлы, мұнда
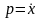– бұрыштың өзгеру жылдамдығы.
жазықтығы фазалық жазықтық деп аталады,
ал
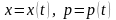параметрлік қозғалыс заңымен анықталатын
қисықтар – фазалық траекториялар.
(2)-теңдеудің аналитикалық шешімі өте күрделі болғандықтан, маятниктің қозғалысын біз сандық түрде зерттейміз. (2)-теңдеуді бірінші ретті теңдеулер жүйесі ретінде жазайық
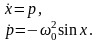(3)
Программаны құруға кірісуден бұрын, қолданатын программалау тіліне сай, есепті тәуелсіз тапсырмалар тізбегіне бөлу керек, яғни алгоритм құрастырылады. Берілген есеп шешімінің программасы келесі бөліктерден тұру керек:
Бастапқы шарттарды белгілеу.
Функцияны белгілеу.
Бойында шешім табылатын кесіндіні және интегралдау қадамын беру (интегралдау қадамын беруден көрі интегралдау кесіндісі бөлінетін интервалдар санын беріп, қадамның мәнін есептеу ыңғайлы).
Дифференциалдық теңдеудің шешімдері анықталатын нүктелердің координаттарын есептеу.
Зерттелетін теңдеуді шешу.
Нәтижені шығару.
MatLabпакетінде кәдімгі дифференциалдық теңдеулерді 4-ретті Рунге-Кутт әдісімен шешу ode45функциясымен іске асырылған. Төменде MatLab тілінде (3)-кәдімгі дифференциалдық теңдеулер жүйесінднің оң жағындағы функцияның анықтамасы келтірілген mayat атты файл-функция, маятниктің қозғалыс теңдеуін сандық шешуге және бейнелеуге арналған программаның мәтіндері берілген. Файл-функциядағы айнымалылар локальды (жергілікті) болғандықтан, оларды глобаль (ауқымды) деп жариялау керек.
function F = mayat(t,y);
global omega;
F=[y(2); - omega^2*sin(y(1))];
Файл-функцияны дискдеміндетті түрде mayat.m атымен сақтау қажет.
Әрі қарай программаның өзін жазамыз:
global omega;
x0 = [2 3];
for omega=1:0.3:4
[T,Y] = ode45('mayat',[0:0.05:4*pi], x0);
hold on
plot(Y(:,1),Y(:,2),'k');
grid on
axis([-5 20 -8 8]);
title('omega=[0;4] үшін бейсызық ...
маятниктің фазалық портреті');
end
Бейсызық маятниктің тепе-тең күйлері фазалық жазықтықта х өсінің х = 0, ± , ±2... нүктелерінде орналасқан. Жүйенің сәйкес фазалық портреті 3-суретте көрсетілген. Ерекше нүктелер х = 0, ± 2, ±4 ... – центр, ал орнықсыз нүктелер х = ± , ±3 ... – ер тоқым тәрізді екені көрінеді.
Центрлер жанында фазалық портрет сапалық түрде сызықты осцилляторға сай: траекториялар түйық концентрлік қисықтар, шеңберлер тәрізді, тербелістердің амплитудасы аз болатын, гармониялық тербелістерге жақын.