
- •Содержание
- •Введение
- •Теоритическая часть
- •Что называется системой линейных уравнений
- •Методы решения систем линейных уравнений
- •Метод Крамера
- •Решение систем линейных уравнений методом обратной матрицы
- •Решение систем линейных уравнений методом Гаусса
- •Практическая часть
- •Решение системы линейных уравнений методом Крамера
- •Решение системы линейных уравнений методом обратной матрицы
- •Решение системы линейных уравнение методом Гаусса
- •Заключение
- •Список использованных источников
Решение системы линейных уравнений методом обратной матрицы
Дана система уравнений (9).
Решение:
Пусть A=(10) – основная матрица системы, Х – матрица-столбец неизвестных системы (9), В – матрица-столбец свободных членов системы (9)
, (12)
 , (13)
, (13)
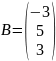 ,
(14)
,
(14)
 (15)
(15)
значит
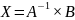 (16)
(16)
Найдем определитель матрицы А

Для нахождения матрицы вычислим алгебраические дополнения для элементов матрицы А

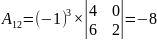

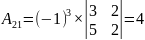





Построим матрицу

Найдем транспонированную матрицу
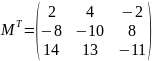
Найдем обратную матрицу

Произведем проверку обратной матрицы, с помощью произведения матрицы на обратную матрицу и наоборот, если результат в обои случаях будет равен единичной матрице, значит обратная матрица найдена верно
С=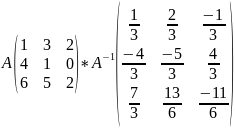


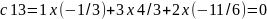



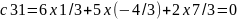
 c33
= 6 x (-1/3) + 5 x 4/3 + 2 x (-11/6) = 1
c33
= 6 x (-1/3) + 5 x 4/3 + 2 x (-11/6) = 1
 =Е
=Е
С=
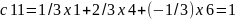






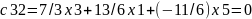 c33
= 7/3 x 2 + 13/6 x 0 + (-11/6) x 2 = 1
c33
= 7/3 x 2 + 13/6 x 0 + (-11/6) x 2 = 1
=Е
Верно, обратная матрица найдена, вычислена правильно.
Находим решение матрицы
=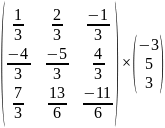 =
= ;
;
Проверка: решенная система ранее была решена методом Крамера с проверкой, решение (текущей) системы методом обратной матрицы совпадает с решением методом Крамера.
Вывод системы решены верно, ответ:
Решение системы линейных уравнение методом Гаусса
Дана система линейных уравнений:

Решение:
Основная матрица системы:
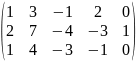
Расширенная матрица системы:

Умножили 1-ую строку на 2
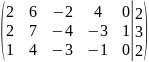
Вычли 1-ую строку из 2-ой и восстановили её

Вычли 1-ую строку из 3-ей

Умножили
2-ую строку на 3

Вычли 2-ую строку из 1-ой строки и восстановили её
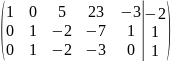
Вычли 2-ую строку из 3-ей

Разделили 3-ю строку на 4
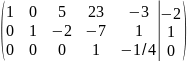
Умножили 3-ю строку на 23
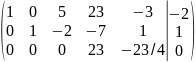
Вычли 3-ю строку из 1-ой строки и восстановили ее

Умножили 3-ю строку на -7
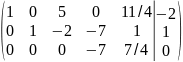
Вычли 3-ю строку из 2-ой строки и восстановили ее

Выразим
из 1-ой строки
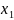

Выразим
из 2-ой строки


Выразим
из 3-ей строки

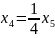


Заключение
В процессе выполнения курсового проекта были закреплены и углублены теоритические знания по дисциплине «Линейная алгебра и аналитической геометрии», а так же были приобретены и закреплены на практике новые навыки по решению систем линейных алгебраически уравнений, следующими методами: методом Гаусса, методом обратной матрицы и методом Крамера.
Список использованных источников
Ильин В. А., Позняк Г. Д. Аналитическая геометрия. — М.: Наука, 1974.
Копылова Т. В. Конспект лекций по линейной алгебре.
Копылова Т. В. Линейная алгебра. — Дубна: Международный университет природы, общества и человека «Дубна», 1996.
Копылова Т. В. Аналитическая геометрия. — Дубна: Международный университет природы, общества и человека «Дубна», 1997.
Ефимова Л. В., Демидович Б. П. Линейная алгебра и основы математического анализа. — М: Наука, 1993.
Мазный Г. Л., Прогулова Т. Б. Методическое пособие к курсовому проектированию по высшей математике и информатике. — Дубна: Международный университет природы, общества и человека «Дубна», 1996.
Калиновский Ю. Л. Конспект лекций по линейной алгебре.
Дубна, 2013
