ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ «Международный университет природы, общества и человека «Дубна»

Институт системного анализа и управления

Кафедра “Конструирование и технология электронных средств”

КУРСОВАЯ РАБОТА

ПО

дисциплине «Линейная Алгебра»

ТЕМА: «Решение систем линейных уравнений»

Выполнил: студент группы 1142

1 Курса ИСАУ

Цветков К.А.

Проверил:

Профессор Калиновский Ю.Л.

Содержание

СОДЕРЖАНИЕ 2

ВВЕДЕНИЕ 3

1 ТЕОРИТИЧЕСКАЯ ЧАСТЬ 4

1.1 Что называется системой линейных уравнений 4

1.2 Методы решения систем линейных уравнений 5

1.2.1 Метод Крамера 5

1.2.2 Решение систем линейных уравнений методом обратной матрицы 7

1.2.3 Решение систем линейных уравнений методом Гаусса 8

2 ПРАКТИЧЕСКАЯ ЧАСТЬ 10

2.1 Решение системы линейных уравнений методом Крамера 10

2.2 Решение системы линейных уравнений методом обратной матрицы 11

2.3 Решение системы линейных уравнение методом Гаусса 14

ЗАКЛЮЧЕНИЕ 18

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 19

Введение

Целью курсовой работы является закрепление и углубление студентом полученных и теоретических знаний и практических навыков по решению систем линейных уравнений, следующими методами: методом Гаусса, методом Крамера и с помощью обратной матрицы.

1. Теоритическая часть

   1. Что называется системой линейных уравнений

Системой m линейных уравнений с n неизвестными называется система вида:

где и (i=1,…,m; b=1,…,n) — некоторые известные числа, а 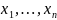— неизвестные. В обозначении коэффициентов первый индекс i обозначает номер уравнения, а второй j — номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы

,

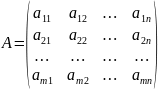которую назовем матрицей системы. Числа, стоящие в правых частях уравнений, 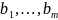называются свободными членами. Совокупность n чисел называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел вместо соответствующих неизвестных .

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.

2. Система может иметь бесконечное множество решений. Например,

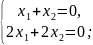
решением которой является любая пара чисел, отличающихся знаком.

3. И третий случай, когда система вообще не имеет решения. Например,

если бы решение существовало, то 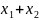равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

2. Методы решения систем линейных уравнений

   1. Метод Крамера

Для решения квадратных систем линейных уравнений вида:

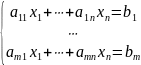(1) с невырожденной основной матрицей используется теорема Крамера:

Если основная матрица квадратной системы линейных уравнений невырожденная, то такая система имеет единственное решение

Доказательство. Пусть A - основная матрица системы (1), Δ - ее определитель (главный определитель системы), X - столбец из ее неизвестных и B — столбец свободных членов системы. Тогда уравнение

(2)

представляет собой матричную запись системы (4.4). Так как по условию теоремы A — невырожденная матрица, то она имеет обратную A-1. Умножим обе части равенства (2) слева на :

A^-1(AX) = A^-1B (3)

Используя ассоциативность умножения матриц, получаем

(A^-1A)X = EX = X = A^-1B (4)

Таким образом,

X = A^-1B (5)

Произведение, стоящее справа, будет матрицей из одного столбца. Ее j - й элемент равен сумме произведений j - й строки матрицы A^-1 на соответствующие элементы матрицы B, т. е. равен числу

(6)

Сумма, стоящая в числителе справа, является, однако, разложением по j - му столбцу определителя Δ, получающегося заменой j - гo столбца определителя Δ столбцом B.

Покажем, что полученные значения неизвестных действительно составляют решение системы (4). Для этого подставим вместо X в матричное уравнение (2) правую часть уравнения (5),

(7)

что приводит к тождеству B = B.

Единственность решения системы (1) следует из единственности обратной матрицы A^-1 и однозначности произведения матриц A^-1B. Учитывая (6), запишем равенства соответствующих элементов матриц — столбцов, расположенных в левой и правой частях матричного равенства (2)

(8)

где Δ j - определители, получающиеся из Δ заменой j - го столбца определителя Δ столбцом B. Равенства (8) называются формулами Крамера решения квадратных систем линейных уравнений, основная матрица которых невырожденная.

Если определитель основной матрицы квадратной системы линейных уравнений равен нулю, то теорему Крамера для нахождения решений системы применять нельзя.