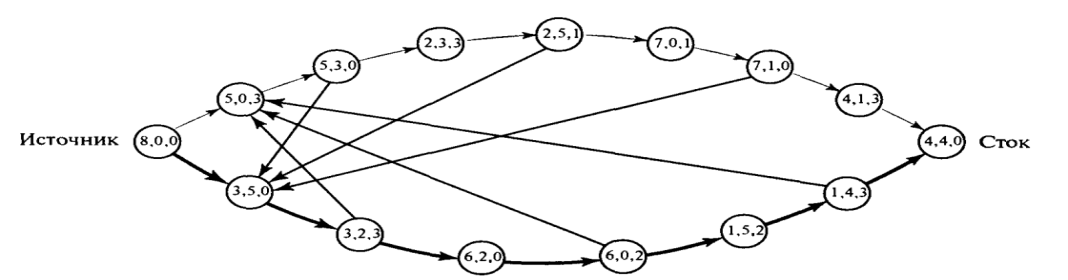
27.Қысқа жол есебі. Дейкстра алгоритмі

Қысқа жол есебі транспорт желісіндегі берілген бастапқы пункт пен көзделген пункт арасындағы қысқа жолды анықтау үшін қолданы-лады. Мұндай моделдерді сан түрлі жағдайларда қолдануға болады. Енді осы есептің кейбір практикалық жағдайларына тоқталалық.

1-сурет. Жабдықты алмастыру есебі қысқа жол іздеу есебі ретінде

2-сурет. Желілік модель

3-сурет. Қысқа жол іздеу есебінің желілік моделі

4-сурет. Үш бидонмен бас қатыру – қысқа жол іздеу есебі.

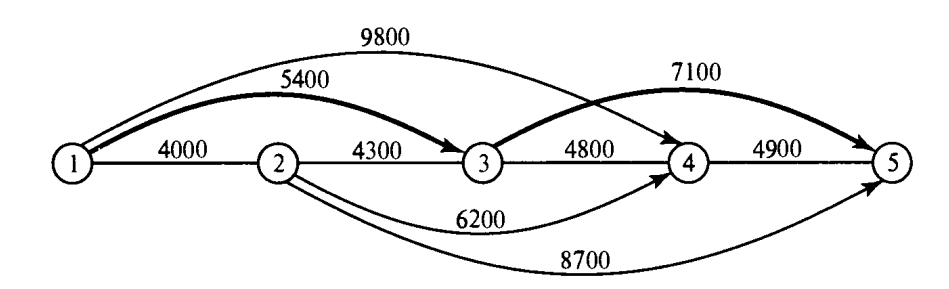
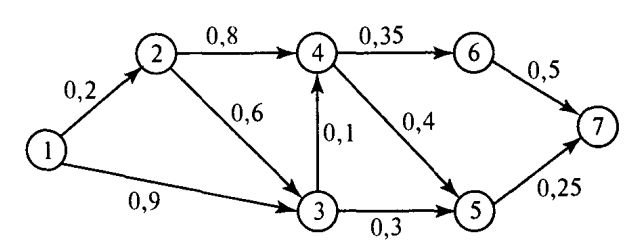
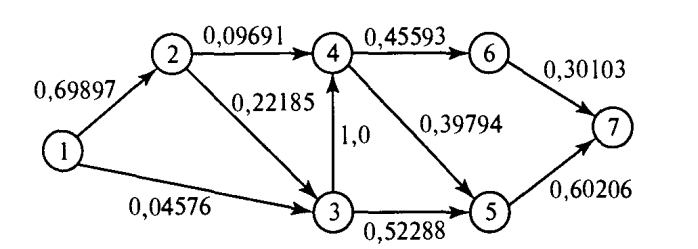
Қысқа жолды анықтау алгоритмдеріне: Дейкстра, Флойд алгоритмдерін жатқызуға болады. Дейкстра алгоритмі бастапқы (1-ші) түйін мен кез-келген басқа түйін арасындағы ең қысқа арақашықтықты табуға арналған.Біз i түйінінен j түйініне жету үшін мынадай белгілеулерді қолданамыз: u_i- 1-ші түйіннен i-ші түйінге дейінгі қысқа қашықтық. d_ij- (i, j) қабырғасының ұзындығы болсын делік, онда j түйінінің таңбасы келесідей анықталады:[u_j, i] = [u_i +d_ij, i], d_ij>= 0.Түйін таңбалары екі түрлі болады: уақытша және тұрақты.Уақытша таңбалар одан да қысқа жол табылғанда келесі уақытша таңбаға ауысады. Ең қысқа жол табылғанда уақытша таңба тұрақты таңбаға ауысады.Дейкстра алгоритмі: 0 кезең. Бастапқы 1 түйінге [0, -] таңбасы беріледі. i = 1 делік. i-ші кезең.а) i түйінінен шығатын барлық уақытша j түйіні үшін [u_i + d_ij, i] таңбасы қарастырылады.Егер j түйінінде k түйінінен алған [u_j, k] таңбасы болса және u_i + d_ij< u_j болса, онда [u_j, k] таңбасы [u_i + d_ij, i] таңбасына ауысады. б)Егер барлық түйіндер тұрақты болса есептеу тоқтатылады.1-ші түйін мен кез келген басқа түйін арасындағы жол (маршрут) ең соңғы түйіннен 1 түйінге дейін тұрақты таңбаларды алып тастап отырғанда дұрыс болса, сол жол шешім болады.

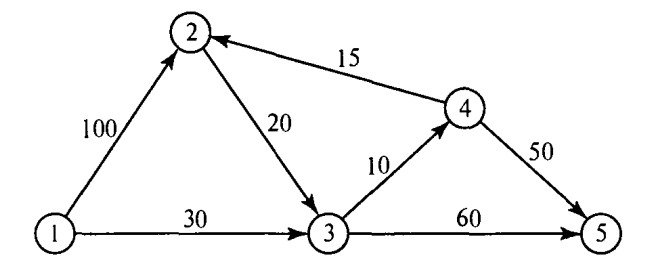
1-сурет. Дейкстра алгоритмі желісінің мысалы.

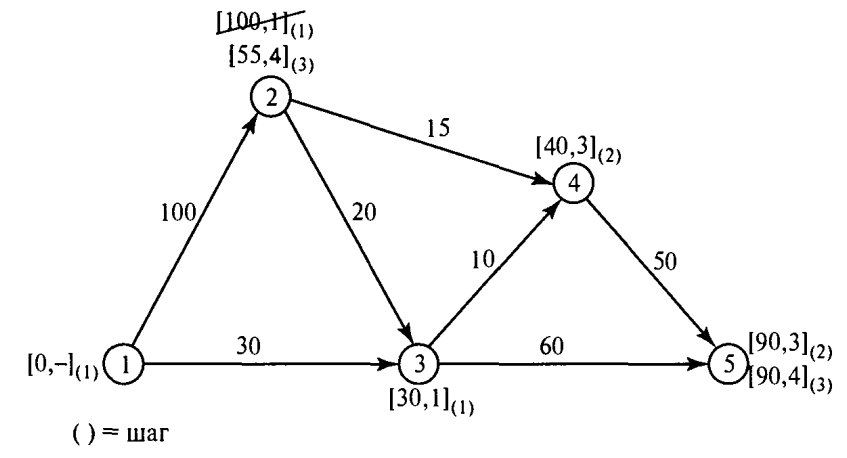
2-сурет. Дейкстра алгоритмін қолдану

28.Сызықтық программалаудағы түйіндестік

Сызықтық программалаудың әрбір есебімен түйіндес деп аталатын сызықтық программалаудың басқа бір есебі тығыз байланысқан. Бастапқы есепті әуелгі дейміз. Әуелгі есеп пен түйіндес есеп арасындағы басты байланыс – олардың бірін тікелей шешу арқылы екіншісінің шешімдерін табуға болатындығында. Кез келген сызықты программалау есебіне сәйкес түйіндес есеп қисындауға болатындығы белгілі. Мәселен жалпы түрдегі сызықты программалаудың әуелгі есебі берілсін

(3.1)

Мұнда үшін теңсіздік түріндегі шектеулер, ал үшін теңдік түріндегі шектеулер жазылған максимумделінетін мақсат функциясы берілген. айнымалалары теріс емес, қалған айнымалылар кез келген таңбалы мәндер қабылдайды. Сонымен қатар мұнда , (теңсіздік түріндегі шектеулер болмайтын), (теңдік түріндегі шектеулер болмайтын ) және (барлық айнымалылар кез келген таңба қабылдайтын), (бар айнымалылар теріс емес) жағдайлары да кездесуі мүмкін. Енді (1) есебіндегі шектеулер жүйесімен анықталатын ұйғарымды шешімдер жиынын арқылы белгілейміз. Сызықты программалаудың түйіндес есебі мына түрде жазылады:

(3.2)

29.Операцияларды зерттеудің типтік есептері

Таңдалған тиімділік принципін (жүйе қызметі сапасының критерийі) сипаттайтын мақсат функциясының түрі операцияларды зерттеу есептерінің типіне байланысты. ОЗ есептерін келесі типтерге бөлеміз:

1) Ықтималдықты есептер (тәуекелмен шешім қабылдау): қай бір стратегияны қабылдағанда мақсатқа жету ықтималдығы белгісіз түрлі нәтижелер алынады;

2) Детерминді есептер (толық анықталғандық шартында шешім қабылдау): әрбір таңдалған стратегия жалғыз нәтижеге соқтырады;

3) Анықталмағандықты есептер (дәлірек айтқанда, анықталмаған-дықта шешім қабылдау есебі): белгілі бір стратегияны қабылдағанда түрлі нәтижелер алынуы мүмкін болса да, мұның ықтималдықты есептерден айырмашылығы: мүмкін нәтижелердің ешқандай статистикалық сипаттарын білмейміз. Анықталмағандық қоршаған орта туралы ешқандай ақпараттартың жоқтығыған, сонымен қатар шешім қабылдау процесінде ескерілетін басқа кісілер (қарсыластар, бәсекелестер, серіктестер) ұстанымының алдын ала белгісіздігінен пайда болады .

Мақсат функциясын таңдау

Ықтималдықты есептерде

стратегиясын қолданғандағы нәтижесін алудың шартты ықтималдығын белгілі деп саналады. Бұл жағдайда мақсат функциясы ретінде

стратегияның күтілетін пайдалылығы , яғни мына түрдегі функция таңдалады:

Е нді тәуекел жағдайында ұтымды ұстаным таңдау үшін тиімділік есебін шығарамыз:

Д етерминдi есептерде

стратегиясын бірге тең ықтималдықпен таңдағанда нәтижесі алынады, сондықтан мақсат функциясы ретінде

түріндегі стратегияның пайдалылығын алып, ең жақсы стратегияны анықтаудың тиімділік есебін қойуға болады:

Анықталмағандықпен шешім қабылдау есептерінде оңтайлы ұстаным критерийлері қолданады.