
- •1.Компакт жиындар
- •2.Вейерштрастың 1-теоремасы
- •3.Тиімділік есебінің қойылымы
- •4.Сызықтық программалау . 3-лемма.
- •5.Сызықтық программалау. 4-лемма
- •7.Вейерштрастың 2-теоремасы.
- •9.Сызықтық программалау. 6-лемма.
- •11.Жатық функциялар дөңестігінің критерийлері. Теорема 1
- •12.Лагранж функциясы. Негізгі теорема.
- •13.Жиынның салыстырмалы ішкі нүктелері.
- •14.Жиынның шекаралық нүктелері
- •15.Дөңес функциялар. 1- теорема.
- •21.Моделдеу принциптері
- •22.Оңтайлы ұстаным критерийлері
- •23.Пайдалылықты өлшеу әдістері
- •24.Көп критерийлі есептер
- •25.Түйіндес симплекс әдіс
- •26.Шекаралар мен тармақтар әдісі
- •27.Қысқа жол есебі. Дейкстра алгоритмі
- •28.Сызықтық программалаудағы түйіндестік
- •29.Операцияларды зерттеудің типтік есептері
- •30.Түйіндес айнымалылардың экономикалық мағанасы
9.Сызықтық программалау. 6-лемма.
10.Тиімділік
критерийі.
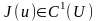 жағдайындағы дөңес программалау
есебі (4) - ке оралайық.
жағдайындағы дөңес программалау
есебі (4) - ке оралайық.
Теорема.
Егер
- еркін функция, U
- дөңес жиын,
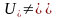 Ø
болса, онда кез келген
,
нүктесінде
Ø
болса, онда кез келген
,
нүктесінде
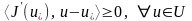 (5)
(5)
теңсіздігі орындалады. Егер дөңес функция, U - дөңес жиын, Ø, онда кез келген нүктесінде (5) шарттың орындалуы қажетті және жеткілікті.
Дәлелі.
Қажеттілігі.
дейік. Кез келген
функциясы үшін (5) өрнек орындалатынын
көрсетейік, мұндағы U
- дөңес жиын. (дербес жағдайда
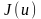 - U
- дағы дөңес функция)
- U
- дағы дөңес функция)
Мәселен,
- еркін нүкте және
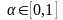 .
Онда
.
Онда
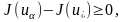 мұндағы
мұндағы
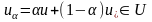 .
Осыдан
.
Осыдан
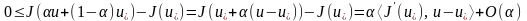
әрі
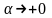 кезінде
кезінде
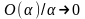 .
Теңдіктің екі жағында
.
Теңдіктің екі жағында
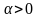 - ға бөліп,
кезіндегі шекке көшсек, (5) өрнекті
аламыз. Қажеттілік дәлелденді.
- ға бөліп,
кезіндегі шекке көшсек, (5) өрнекті
аламыз. Қажеттілік дәлелденді.
Жеткіліктілігі.
дөңес функция, U
- дөңес жиын,
Ø
және (5) өрнек орындалсын.
екенін көрсетейік. Мәселен,
- еркін нүкте. Онда 2 - теоремаға сай
(«Тегіс функциялардың тиімділігінің
баламасы» бөлімін қараңыз) алатынымыз
барлық
кезінде
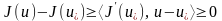 .
Осыдан шығатыны:
.
Осыдан шығатыны:
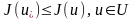 .
Демек,
.
Теорема дәлелденді.
.
Демек,
.
Теорема дәлелденді.
Салдар.
Егер
,
U
- дөңес жиын,
Ø
және
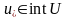 ,
онда
,
онда
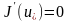 теңдігінің орындалуы қажет.
теңдігінің орындалуы қажет.
Шынында
да, егер
,
онда барлық
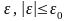 кезінде
кезінде
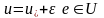 болатын кез келген
болатын кез келген
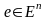 үшін
үшін
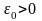 саны табылады. Сонда (5) - тен барлық
кезінде де
саны табылады. Сонда (5) - тен барлық
кезінде де
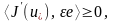 ,
,
 .
Осыдан алатынымыз:
.
.
Осыдан алатынымыз:
.
Осы (5) формула сызықсыз программалау есебі тиімділігінің қажетті шарты ретінде және дөңес программалау есебі тиімділігінің қажетті де жеткілікті шарты ретінде келесі лекцияларда қолданыс табады.
11.Жатық функциялар дөңестігінің критерийлері. Теорема 1
12.Лагранж функциясы. Негізгі теорема.
L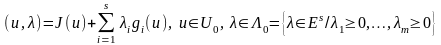 (3)
(3)
функциясын (1), (2) есебінің Лагранж функциясы деп атайды.
1-анықтама.
Егер
L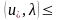 L
L L
L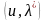 ,
,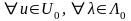 .
(4)
.
(4)
шарты
орындалса, онда
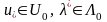 ,
яғни
,
яғни
 жұбы (3) -Лагранж функциясының қайқы
нүктесі деп аталады.
жұбы (3) -Лагранж функциясының қайқы
нүктесі деп аталады.
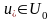 нүктесінде
L
функциясы
нүктесінде
L
функциясы
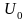 жиынында минимумға жететінді-гін
байқаймыз.
Ал
жиынында минимумға жететінді-гін
байқаймыз.
Ал
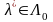 нүктесінде
жиынындағы L
нүктесінде
жиынындағы L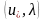 функциясының
максимумын аламыз. Лагранж функциясының
анықталу облысы
функциясының
максимумын аламыз. Лагранж функциясының
анықталу облысы
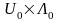 жиыны болып табылады.
жиыны болып табылады.
Негізгі
теорема.
Егер
жұбы (3) - Лагранж функциясының қайқы
күктесі болса, онда
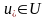 векторы (1), (2) есебінің шешімі болады.
Яғни
векторы (1), (2) есебінің шешімі болады.
Яғни
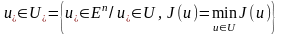 .
.
Дәлелі.
жұбы үшін (5), (6) шарттарының орындалаты-ны
негізгі леммадан көрініп. Ендеше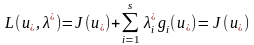 .
Енді (5) теңсіздік былай жазылады:
.
Енді (5) теңсіздік былай жазылады:
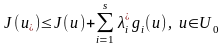 .
(9)
.
(9)
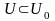 болғандықтан
(9) теңсіздік дербес жағдайда барлық
болғандықтан
(9) теңсіздік дербес жағдайда барлық
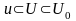 орындалады, яғни
орындалады, яғни
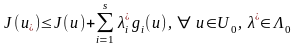 .
(10)
.
(10)
Енді
2-шарттан аңғаратынымыз: егер
онда
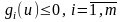 және
және
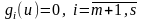 :
демек кез келген
:
демек кез келген
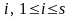 үшін
үшін
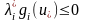 .
Ескеретініміз
.
Ескеретініміз
 ,
мұндағы
,
мұндағы
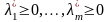 .
Ендеше (10)-нан шығатыны
.
Ендеше (10)-нан шығатыны
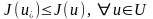 .
Бұл
нүктесінде
функциясы U
жиынындағы глобәлдік немесе абсолют
минимумға жететіндігің білдіреді.
Теорема дәлелденді.
.
Бұл
нүктесінде
функциясы U
жиынындағы глобәлдік немесе абсолют
минимумға жететіндігің білдіреді.
Теорема дәлелденді.
13.Жиынның салыстырмалы ішкі нүктелері.
14.Жиынның шекаралық нүктелері
15.Дөңес функциялар. 1- теорема.
1
анықтама.
-
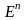 -дегі дөңес
жиынында анықталған функция болып, кез
келген
-дегі дөңес
жиынында анықталған функция болып, кез
келген
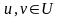 нүктелері үшін барлық
нүктелері үшін барлық
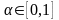 кезінде
кезінде
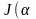
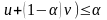
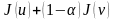 (1)
(1)
теңсіздігі
орындалса, онда
функциясы
жиынындағы дөңес функция деп аталады.Егер
(1) өрнектегі теңдік тек
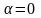 және
және
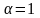 кезінде ғана мүмкін болса, онда
функциясы дөңес
жиынындағы қатаң дөңес функция болғаны.
Егер дөңес
жиынында
функциясы дөңес (қатаң дөңес) болса,
онда –
функциясы ойыс (қатаң ойыс) болғаны.
кезінде ғана мүмкін болса, онда
функциясы дөңес
жиынындағы қатаң дөңес функция болғаны.
Егер дөңес
жиынында
функциясы дөңес (қатаң дөңес) болса,
онда –
функциясы ойыс (қатаң ойыс) болғаны.
2 анықтама. дөңес жиынында анықталған функция болсын.
Егер кез келеген нүктелері үшін барлық кезінде
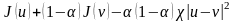 (2)
(2)
теңсіздігі
орындалатын
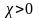 саны табылса, онда
саны табылса, онда
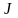 функциясы
жиынында әлді дөңес функция делінеді.
функциясы
жиынында әлді дөңес функция делінеді.
1
теорема.
Дөңес
жиынында
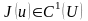 функциясы дөңес болуының қажетті де
жеткілікті шарты:
функциясы дөңес болуының қажетті де
жеткілікті шарты: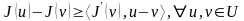 (4)
Дәлелі.
Кажеттілігі.
дөңес дейік. Сонда (1) теңсіздігінен
алатынымыз:
(4)
Дәлелі.
Кажеттілігі.
дөңес дейік. Сонда (1) теңсіздігінен
алатынымыз: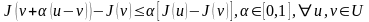
Осыдан, ақырлы өсімшелер формуласы негізінде жазатынымыз:
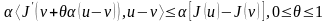 Бұл
теңсіздіктің екі жағын да
санға бөліп,
кезде шекке көшіп,
екендігін ескерсек (4) өрнегі
шығады.Қажеттілік
дәлелденді.
Бұл
теңсіздіктің екі жағын да
санға бөліп,
кезде шекке көшіп,
екендігін ескерсек (4) өрнегі
шығады.Қажеттілік
дәлелденді.
Жеткіліктілігі
.
Дөңес
жиынындағы
функциясы үшін (4) өрнегі орындалсын.
Онда
- да
функциясының дөңестігін көрсетейік.
дөңес болғандықтан:
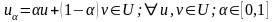 .
.
Ендеше
(4) теңсіздігінен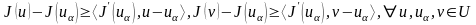 .
Бірінші теңсіздікті
.
Бірінші теңсіздікті
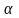 - ға, ал екінші теңсіздікті
- ға, ал екінші теңсіздікті
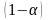 санына көбейтіп, оларды қосамыз.
Нәтижесінде алатынымыз:
санына көбейтіп, оларды қосамыз.
Нәтижесінде алатынымыз:
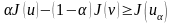 .
Бұдан
функциясының
жиынында дөңестігі шығады. Теорема
дәлелденді.
.
Бұдан
функциясының
жиынында дөңестігі шығады. Теорема
дәлелденді.
16.Дөңес
программалау есебін шығару алгоритмі.
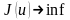 (23)
(23)
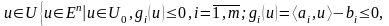
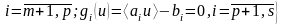 есебі
үшін
екендігіне көз жеткізу керек. Ол үшін
1-3 тh (Вейерштрасс тh) қолданамыз.Дөңес
программалау есебінің түріне
байланысты Лагранж фун қайқы нүктесінің
болатындығына кепілдік беретін шарттардың
орындалуын тексереміз .Мысалы, егер
есеп (1)-(2 түрінде болса, онда
регуляр
екендігін , егер есеп (8)-(9) түрінде болса,
онда
есебі
үшін
екендігіне көз жеткізу керек. Ол үшін
1-3 тh (Вейерштрасс тh) қолданамыз.Дөңес
программалау есебінің түріне
байланысты Лагранж фун қайқы нүктесінің
болатындығына кепілдік беретін шарттардың
орындалуын тексереміз .Мысалы, егер
есеп (1)-(2 түрінде болса, онда
регуляр
екендігін , егер есеп (8)-(9) түрінде болса,
онда
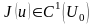 екендігін, ал (23)-(24) есебі үшін
екендігін, ал (23)-(24) есебі үшін
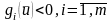 орындалатын
орындалатын
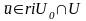 нүктесі табылатындығын көрсетеміз.
Анықталу
аймағы
Лагранж
нүктесі табылатындығын көрсетеміз.
Анықталу
аймағы
Лагранж
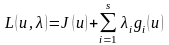 құрамыз, мұн.
құрамыз, мұн.
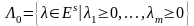 .
.
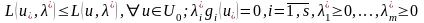 (26)
шартынан (негізгі лемма) Лагранж
фун
қайқы нүктесін табамыз. а) 1-ші шарттан
көретініміз
(26)
шартынан (негізгі лемма) Лагранж
фун
қайқы нүктесін табамыз. а) 1-ші шарттан
көретініміз
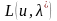 функциясы
жиынындағы минимумына
функциясы
жиынындағы минимумына
 нүктесінде жетеді.
нүктесінде жетеді.
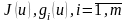 функциялары дөңес
жиынындағы дөңес функциялар, ендеше
-да
дөңес. Егер
функциялары дөңес
жиынындағы дөңес функциялар, ендеше
-да
дөңес. Егер
 ,
онда тиімділік баламасы бойынша және
глобәлдік минимум туралы теоремадан
(26)-дағы 1-ші шартты мынаған алмастырамыз:
,
онда тиімділік баламасы бойынша және
глобәлдік минимум туралы теоремадан
(26)-дағы 1-ші шартты мынаған алмастырамыз:
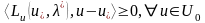 ;
мұндағы
;
мұндағы
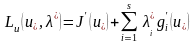 .
Енді (26)
.
Енді (26)
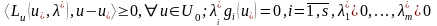 (27) түрінде жазылады. б) Егер
(27) түрінде жазылады. б) Егер
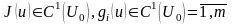 сыртында
сыртында
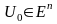 ,
онда тиімділік баламасына сай (27) шартын
келесі түрде өрнектейміз:
,
онда тиімділік баламасына сай (27) шартын
келесі түрде өрнектейміз:
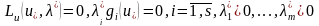 (28) Соңғы (28) шарты
(28) Соңғы (28) шарты
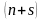 алгебралық теңдеулер жүйесін білдіреді,
белгісіздер саны:
алгебралық теңдеулер жүйесін білдіреді,
белгісіздер саны:
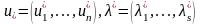 .
Байқайтынымыз: егер Лагранж фун қайқы
нүктесі бар болса, онда (28) - теңдеулер
жүйесінің шешімі бар болғаны, әрі
.
Байқайтынымыз: егер Лагранж фун қайқы
нүктесі бар болса, онда (28) - теңдеулер
жүйесінің шешімі бар болғаны, әрі
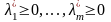 орындалу керек. (28)-шарт
орындалу керек. (28)-шарт
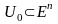 жағдайында қолданылады, дегенмен бұл
жағдайда
екендігіне көз жеткізу керек.
Мәселен
жұбы анықталады дейік. Онда
нүктесі мен
жағдайында қолданылады, дегенмен бұл
жағдайда
екендігіне көз жеткізу керек.
Мәселен
жұбы анықталады дейік. Онда
нүктесі мен
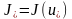 шамасы тиімділік есебінің шешімі
шамасы тиімділік есебінің шешімі
17.Кун-Таккер
теорамасы қандай есепте қолданылады?
Қандай
шарттар орындалғанда Лагранж функциясы
қайқы нүктеге ие болатындығын тағайындайтын
теоремалар Кун-Таккер теоремалары деп
аталады.
Кейде
бастапқы есептің шешімі бар болып (яғни
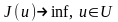 ,
,
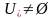
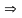 ),
ал осы есеп үшін Лагранж функциясының
қайқы нүктесі жоқ болуы мүмкін.
),
ал осы есеп үшін Лагранж функциясының
қайқы нүктесі жоқ болуы мүмкін.
1-жағдай. Дөңес программалаудың келесі есебін қарастырайық
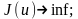 (1)
(1)
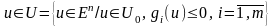 (2)
мұндағы
(2)
мұндағы
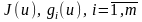 -
жиынында анықталған дөңес функциялар.
-
жиынында анықталған дөңес функциялар.
1
анықтама.
Егер
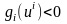 болатын
болатын
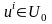 нүктесі табылса, онда
нүктесі табылса, онда
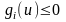 шектеуі
жиынында регуляр делінеді. Егер барлық
(2) шартындағы
шарттары
жиынында регуляр болса,онда U
регуляр
жиын
деп аталады.
шектеуі
жиынында регуляр делінеді. Егер барлық
(2) шартындағы
шарттары
жиынында регуляр болса,онда U
регуляр
жиын
деп аталады.
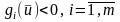 (3)
(3)
орындалатын
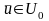 нүктесі бар болсын. Осы (3) шарты Слейтер
шарты деп аталады.
нүктесі бар болсын. Осы (3) шарты Слейтер
шарты деп аталады.
1 теорема. Егер - дөңес жиынында анықталған функциялар, U жиыны регуляр және , онда әрбір нүктесі үшін жұбы Лагранж функциясының:
L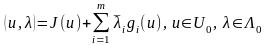 қайқы
нүктесін құратын Лагранж көбейткіштері
қайқы
нүктесін құратын Лагранж көбейткіштері
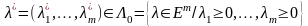 табылуы қажетті. Теорема шартынан
байқайтынымыз: дөңес программалау есебі
(1), (2) үшін егер U
жиыны регуляр
болса (
шарты орындалғанда) Лагранж функциясы
қайқы нүктеге ие болады екен.
табылуы қажетті. Теорема шартынан
байқайтынымыз: дөңес программалау есебі
(1), (2) үшін егер U
жиыны регуляр
болса (
шарты орындалғанда) Лагранж функциясы
қайқы нүктеге ие болады екен.
II жағдай. Енді дөңес программалаудың келесі есебін қарастырайық: (8)
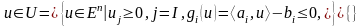 (9)
(9)
мұндағы
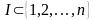 - жиынша,
- жиынша,
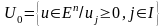 жиын,
-дөңес
жиынында анықталған дөңес функция,
жиын,
-дөңес
жиынында анықталған дөңес функция,
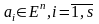 берілген векторлар,
берілген векторлар,
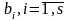 берілген сандар. Осы (8), (9) есебі үшін
Лагранж функциясын жазайы
L
берілген сандар. Осы (8), (9) есебі үшін
Лагранж функциясын жазайы
L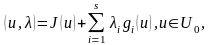
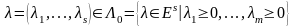 (10)
(10)
Егер
функция
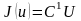 сызықты болса, онда (8)-(9) есебі сызықты
программалаудың жалпы есебі деп аталады.
Мәселен
сызықты болса, онда (8)-(9) есебі сызықты
программалаудың жалпы есебі деп аталады.
Мәселен
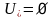 делік. Жоғарыдағы (8)-(9) есебі үшін жазылған
Лагранж функциясы (10) дөңес U
жиынына қосымша ешқандай шарт
қойылмаса да қайқы нүктеге ие болады
екен.
делік. Жоғарыдағы (8)-(9) есебі үшін жазылған
Лагранж функциясы (10) дөңес U
жиынына қосымша ешқандай шарт
қойылмаса да қайқы нүктеге ие болады
екен.
2
теорема. Егер
дөңес
жиынындағы дөңес функция,
және (8) - (9) есебі үшін
болса, онда әрбір
нүктесі үшін
жұбы (10) - Лагранж функциясының
жиынындағы қайқы нүктесін құратын
Лагранж көбейткіштері
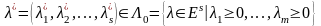 табылуы қажет.
табылуы қажет.
3-жағдай. Дөңес программалаудың неғүрлым жалпы есебін қарастырайық
(23) (24)
мұндағы
дөңес
жиынында анықталған дөңес функциялар,
 - берілген векторлар,
- берілген векторлар,
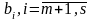 берілген сандар. Осы (34)-(35) есебі үшін
Лагранж функциясы:
берілген сандар. Осы (34)-(35) есебі үшін
Лагранж функциясы:
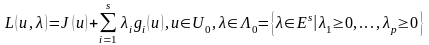 (25)
(25)
3
теорема.
Егер
дөңес
жиынындағы анықталған дөңес функциялар;
(34)-(35) есебі үшін
және
орындалатын
нүктесі табылса, онда әрбір
нүктесі үшін
жұбы
жиынында (36)-Лагранж функциясының қайқы
нүктесін құратын Лагранж көбейткіштері
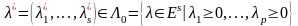 табылуы қажетті.
табылуы қажетті.
18.Операцияларды
зерттеудің кезеңдері Операцияларды
зерттеу – ұйымдастыру жүйелеріндегі
тиімді басқарудың әдістерін жасап, оны
іске асырумен айналысатын ғылым.
Операцияларды зерттеу-дің мақсаты –
ұйымдастыру жүйелерін басқаруда
қабылданатын шешімдерді сандық түрде
негіздеу.Белгілі бір мақсатқа жетуге
бағышталған әрекеттердің мен шаралардың
жиынтығын операция деп түсінеміз.
«Операцияларды зерттеу» өзіндік
зерттеу нысаны мен әдіснамасы бар
кешенді ғылыми зерттеулердің қатарына
жатады. Мәселені шешуге сан қилы
міндеттерді (экономикалық, физикалық,
биологиялық және басқа) позицияда
талдайтын кешенді ғылыми-зерттеуші
ұжымдар қатысады. Операциялық топтар
құрамы түрлі білім салаларының
мамандарынан: математиктерден,
инженерлер-ден, экономистерден,
әлеуметтанушылардан, психологтардан
т.с.с. тұрады. Осындай топтарды құру
мақсаты – проблеманы шешуге ықпалды
барлық факторлар жиынын кешенді түрде
зерттеу және әр алуан ғылымның идеялары
мен әдістерін қолдану. ОЗ әдіснамасы-ның
екінші ерекшелігі – моделдерді және
есептеу техникасын қолдануы. Операциялық
моделдердің құраушылары: а) жүйенің
қызмет ету сапасын сипаттайтын критерий: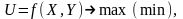 мұндағы
– басқарылатын айнымалылар,
мұндағы
– басқарылатын айнымалылар,
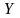 – басқарылмайтын айнымалылар;
– басқарылмайтын айнымалылар;
б) басқарылатын айнымалылардың өзгеру межелерін анықтайтын теңдеулер мен теңдіктер түріндегі шектеулер.Есептің мағанасына қарай математикалық анализдің немесе экстремалдік есептерді шешудің әдістерін қолданып, берілген шарттар мен шектеулердегі сапа критерийін максимумдайтын немесе минимумдайтын тиімді шешімді табамыз. Зерттелінетін моделіміз нақты жүйені мейлінше дәл бейнелегенде ғана шешім нәтижесінде алынған айнымалылардың тиімді мәні жүйенің қызмет ету сапасы жақсаратындықтан, моделдің нақтылыққа сәйкестігін тексеріп, алынған шешімді бағалау қажет.
Ақырында, ОЗ мақсаты нақты жүйелердің қызметінің сапасын жақсартуды көздейтіндіктен, зерттеу нәтижелері қолданысқа енуі тиіс.Сонымен, кез келген операцияны зерттеу келесі кезеңдерден тұрады:1.мәселенің қойылуы; 2.моделді құру; 3.шешім алу; 4.моделді тексеру және шешімді бағалау;5.нәтижелерді қолданысқа енгізу.
20.Сызықтық
программалаудың канондық есебін қай
әдіспен шығарамыз?Канондық
түрдегі сызықты программалау есебін
қарастырайық: , (2.12)мұндағы
, (2.12)мұндағы
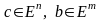 -
берілген векторлар, А- берілген
-
берілген векторлар, А- берілген
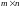 ретті матрица.
ретті матрица.
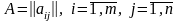 матрицасын
матрицасын
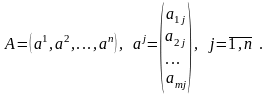
түрінде
жазуға
болады.
Мұндағы
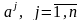 векторы
шарттар
векторлары
деп,
ал
векторы
шарттар
векторлары
деп,
ал
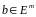 - шектеулер
векторлары
деп
аталады.
Ендеше
- шектеулер
векторлары
деп
аталады.
Ендеше
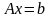 теңдеуі
теңдеуі
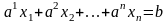 түрінде
жазылады.
Мына
түрінде
жазылады.
Мына
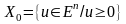 ,
,
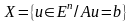 жиындары
аффиндік
жиындар,
яғни
дөңес
жиындар.
жиындары
аффиндік
жиындар,
яғни
дөңес
жиындар.
1
анықтама.
Егер
нүктесі
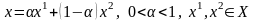
түрінде өрнектелмесе, онда ол шеткі (немесе бұрыштық) нүкте деп аталады.Осы анықтамадан шеткі нүкте жиынындағы кесінділердің ешқайсысының ішкі нүктесі болмайтындығын көреміз. 1 Лемма. Шеткі нүктенің оң координаттарының саны m - нен аспайды. 2 Лемма. Шеткі нүктенің оң координаттарына сай шарттар векторлары сызықты тәуелсіз.
2-анықтама.
Егер ұйғарымды векторлардың оң
координаттарының саны А матрицасының
рангынан кем болмаса (яғни
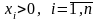 ,
тендеуіндегі нөлден ерекше қосылғыштар
А матрицасының рангынан кем болмаса),
онда (2.12) -түрдегі есеп сызықты
программалаудың канондық түрдегі
ерекшеленбеген есебі деп аталады.
,
тендеуіндегі нөлден ерекше қосылғыштар
А матрицасының рангынан кем болмаса),
онда (2.12) -түрдегі есеп сызықты
программалаудың канондық түрдегі
ерекшеленбеген есебі деп аталады.
3-лемма. Айталық . Егер ерекшеленбеген есептегі ұйғарымды векторының дәл m оң координаты болса, онда х - Х жиынындағы шеткі нүкте.
4-лемма. Кез келген нүктесін жиынындағы шеткі нүктелердің дөңес сызықты комбинациясы ретінде өрнектеуге болады, яғни - жиынындағы шеткі нүктелер.
