1.Компакт жиындар
Тиімділік есебін қарастырайық:
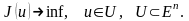(1)
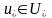нүктесін
және
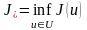шамасын табу қажет. Егер
онда
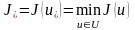екендігін байқаймыз.
Компакт
жиындар.
Мәселен
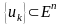қандай да бір тізбек болсын.Онда еске
сала кететініміз: а) егер
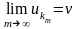орындалатын
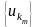тізбекшесі табылатын болса, онда
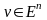нүктесі
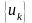тізбегінің шекті нүктесі деп аталады;
б) барлық
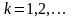үшін
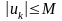болатын
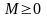саны табылса, онда
тізбегін шектелген дейміз; в) егер
барлық
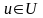үшін
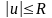орындалатын
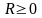саны табылса, онда
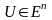жиыны
шектелген делінеді; г) егер
нүктесінің
кез келгек
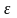- аймағы (O(V,
)
жиыны) U
жиынының
-
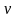дан өзге нүктелерін қамтыса, онда
нүктесі U
жиынының шекті нүктесі деп аталады;
д) U
жиынының кез келген
шекті нүктесі үшін
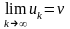болатын
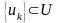тізбегі табылады; е) егер
жиыны өзінің барлық шекті нүктелерін
қамтыса, онда бұл жиын тұйық жиын деп
аталады.
1
анықтама.
Егер кез келген
тізбегі ең болмағанда бір шекті
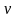нұктесін қамтыса және
,
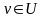онда
жиыны компакт жиын деп аталады.
Бұл анықтама математикалық анализ курсындағы "кез келген шектелген, әрі тұйық жиын - компакт жиын" деген тұжырыммен мағыналас екендігін көреміз. Шынында да, Больцано-Вейерштрасс теоремасына сай кез келген шектелген тізбектің ең болмағанда бір шекті нүктесі бар (U жиыны шектелген), ал тиістілігінен U жиынының тұйықтығы шығады.
2.Вейерштрастың 1-теоремасы
1
теорема.
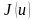функциясы компакт
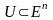жиынында анықталған, ақырлы және
төменнен жартылай үзіліссіз дейік. Онда
жиыны
бос
емес,
компакт жиын
және
кез
келген
минимумдаушы
тізбек
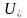жиынына
жинақталады.
Дәлелі:
кез
келген
минимумдаушы
тізбек,
яғни
сандық
тізбектің
шегі
.
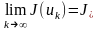Мұндай
минимумдаушы
тізбек
әрқашанда
бар
болатынын
байқаймыз.
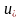- минимумдаушы
тізбектің
кез
келген
шекті
нүктесі
дейік.
Демек,
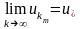болатын
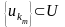тізбекшесі
табылады.
U
жиыны
компакт, сондықтан
минимумдаушы
тізбектің
барлық
шекті
нүктелері
U
жиынында
жатады.
Төменгі
мән және
функциясының
төменнен
жартылай
үзіліссіздігі
анықтамасынан
келесі
теңсіздіктер
шығады:
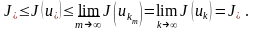(2)
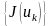тізбегі
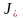шамасына
жинақталатындықтан,
оның
кез
келген
тізбекшесі
де
шамасына
жинақталады.
Соңғы
(2) теңсіздігінен
алатынымыз:
Демек.,
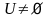және
.
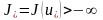Осы
тұжырым
минимумдаушы
тізбектің
кез
келген
шекті
нүктесі
үшін
әділ
болғандықтан
U
- дағы
кез
келген
минимумдаушы
тізбек
жиынына
жинақталады.
жиыны
компакт екендігін
көрсетейік.
-
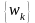жиынынан
алынған
кез
келген
тізбек
дейік.
тиістілігінен
шығатыны:
.
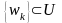Ендеше,
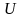жиыны
компакт
болғандықтан
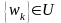нүктесіне
жинақталатын
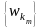тізбекшесі
табылады.
болғандықтан
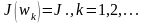
Демек,
минимумдаушы
тізбек.
Онда
жоғарыдағы
дәлелдеуден
көретініміз:
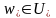шекті
нүкте.
Сонымен,
жиынының
тұйықтығы
дәлелденді.
жиынының
шектелгендігі
тиістілігінен
шығады.
жиыныны
компакт
екендігі
дәлелденді.
Теорема
дәлелденді.
Қолданбалы есептердің көбінде жиыны шектелмеген. Мұндай жағдайларда келесі теоремалардың көмегі тиеді.
3.Тиімділік есебінің қойылымы
4.Сызықтық программалау . 3-лемма.
Айталық
.
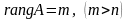Егер
ерекшеленбеген
есептегі
ұйғарымды
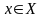векторының
дәл
m оң
координаты
болса,
онда
х
- Х
жиынындағы
шеткі
нүкте.