5.2 Прогнозирование функции отклика объекта на изменение его геометрических свойств.
В данном случае элементами предыстории будут являться значения ΔPx, ΔPy, ΔPz, γ, β, δ, ΔL/3, Δ|R|, S на 14 моментов времени. Необходимо спрогнозировать состояние объекта на 15й момент времени, построить графики с прогнозными точками в фазовом пространстве и произвести оценку прогнозных значений.
(8)
(9)
Производим расчет прогнозных значений µ и α как реальных, так и предельных (µа, µв, αа, αв), при; А=0,3; А=0,7; А=0,9 для массива данных Н,Х,Y. Результаты вычислений приведены в таблицах на рисунках 10,11 .
По полученным данным строим графики прогнозирования экспоненциальным сглаживанием, которые изображены на рисунках 18-26.
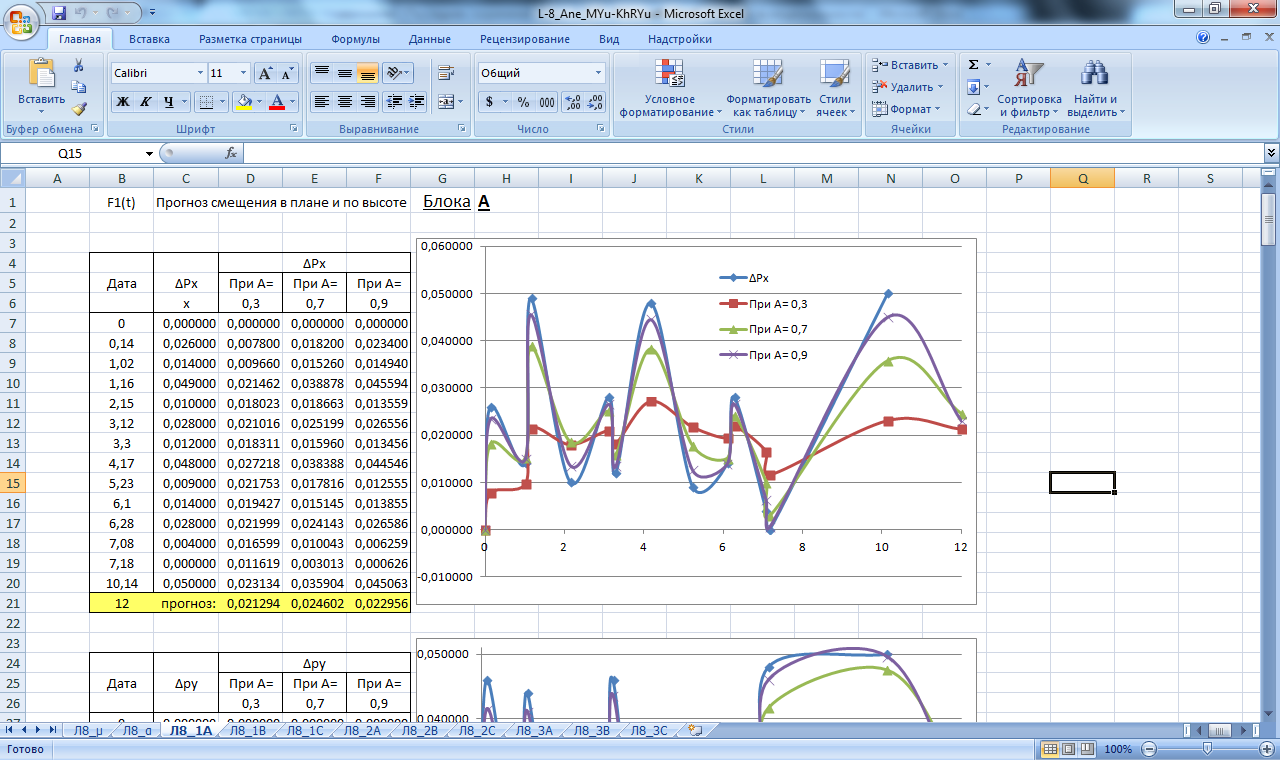
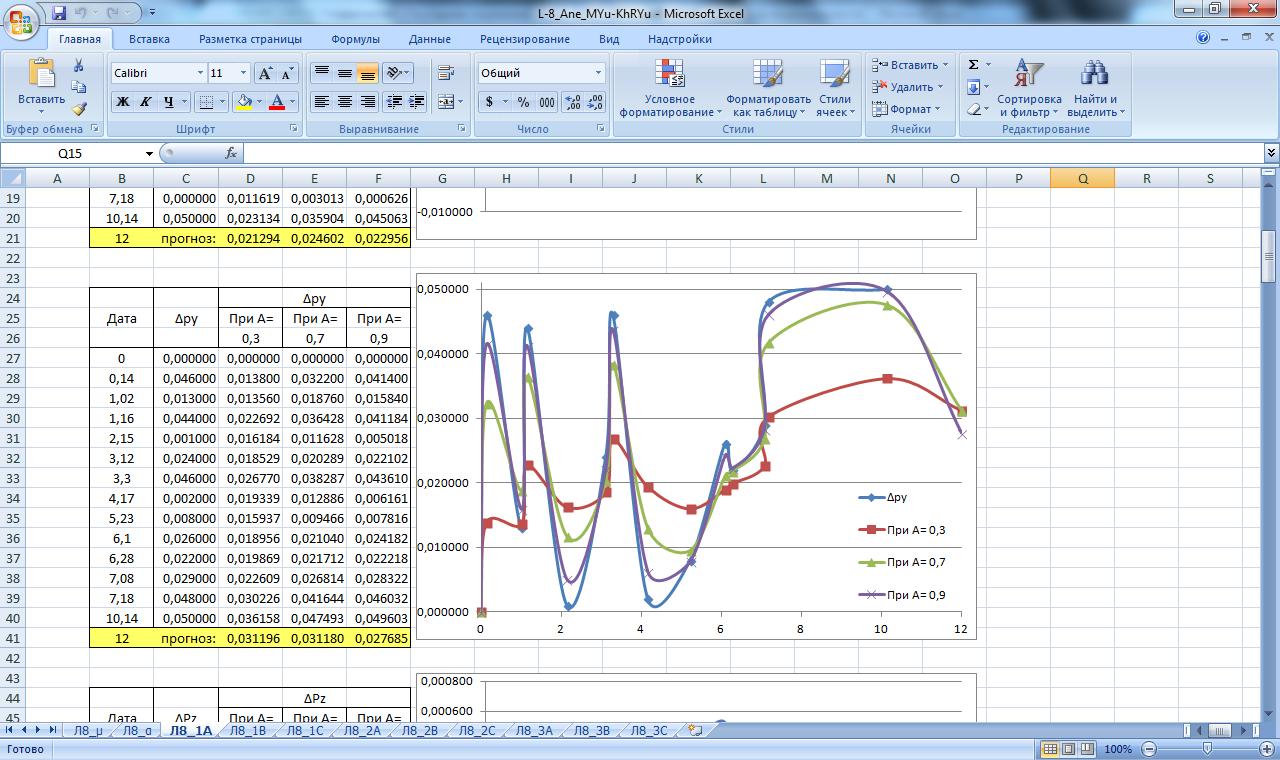
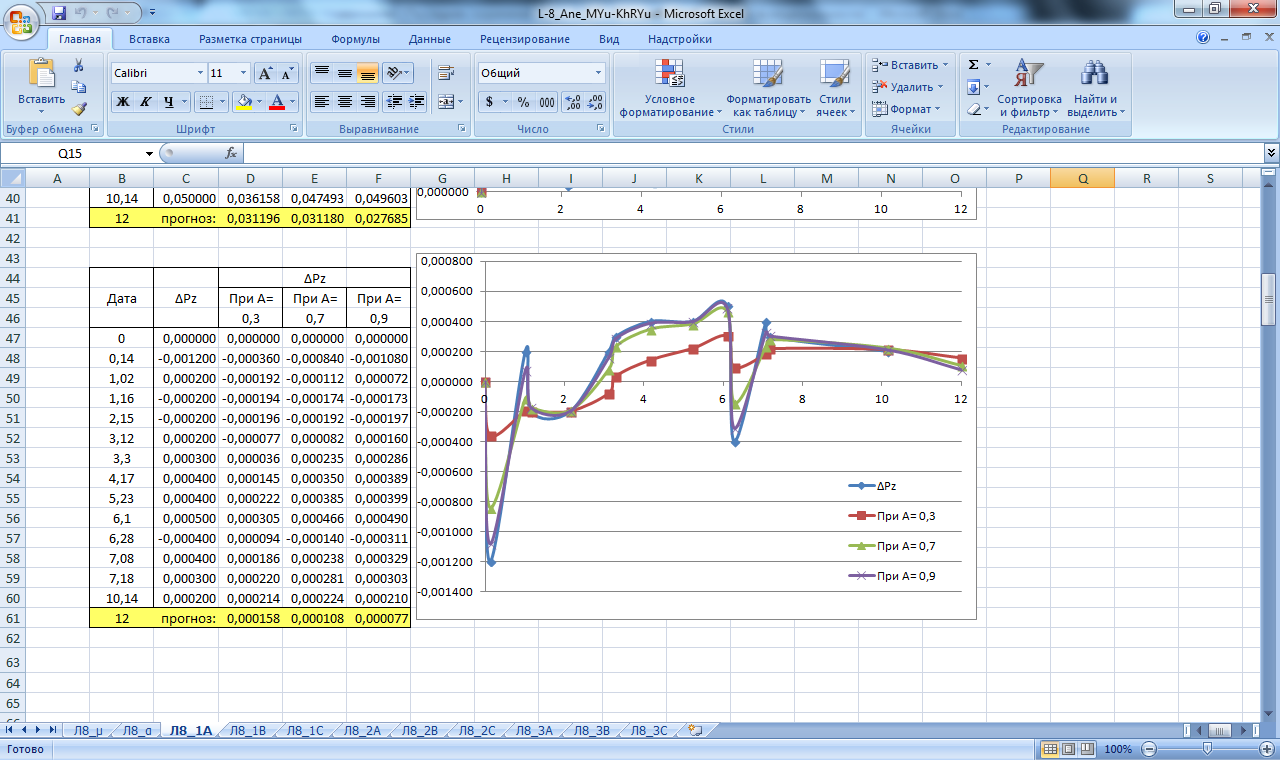
Рисунок 18. Значение сглаживающей функции прогноза смещения в плане и по высоте блока А. Прогнозирование экспоненциальным сглаживанием.
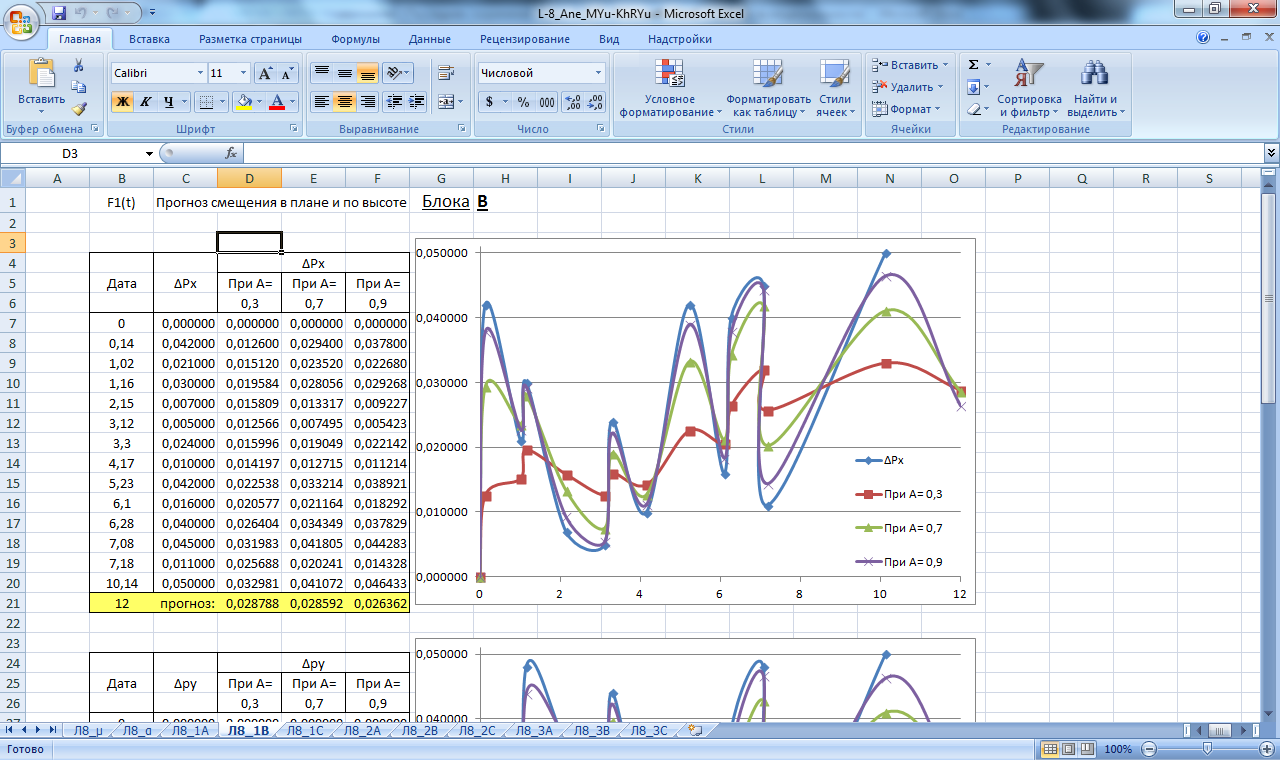
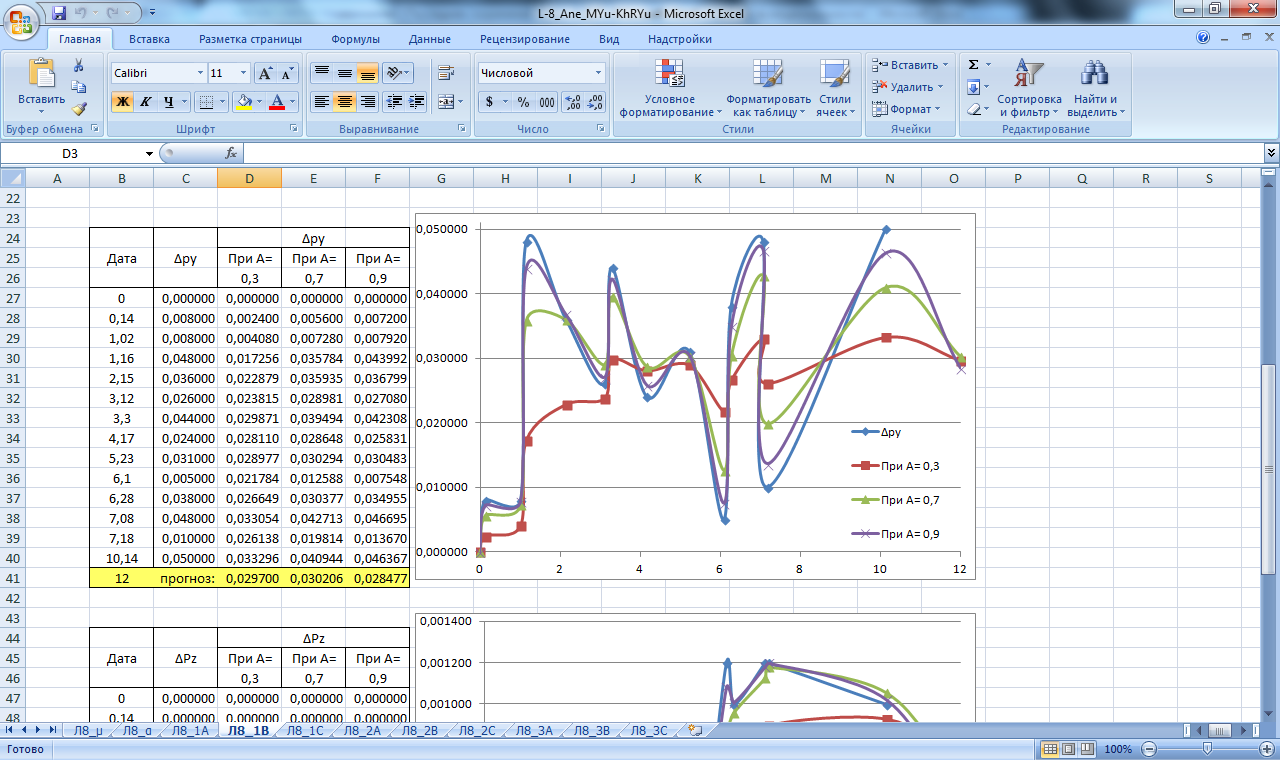
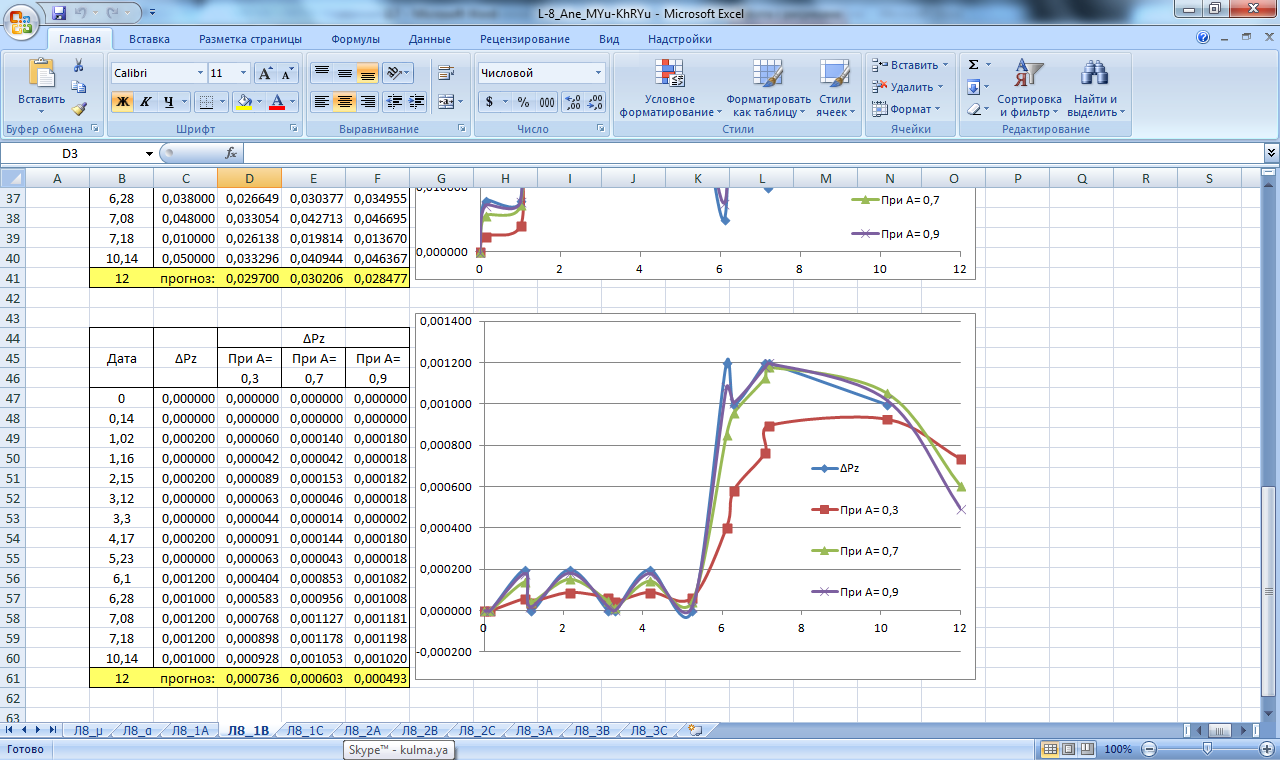
Рисунок 19. Значение сглаживающей функции прогноза смещения в плане и по высоте блока В. Прогнозирование экспоненциальным сглаживанием
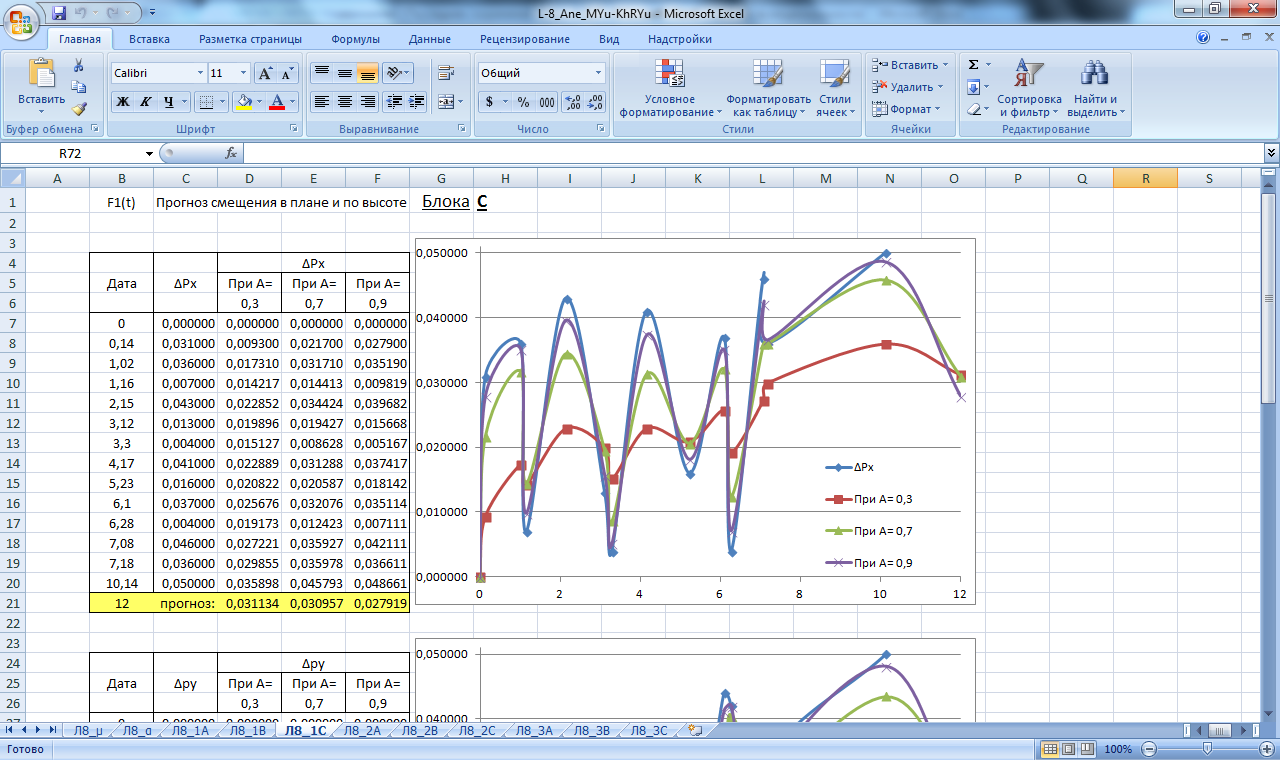
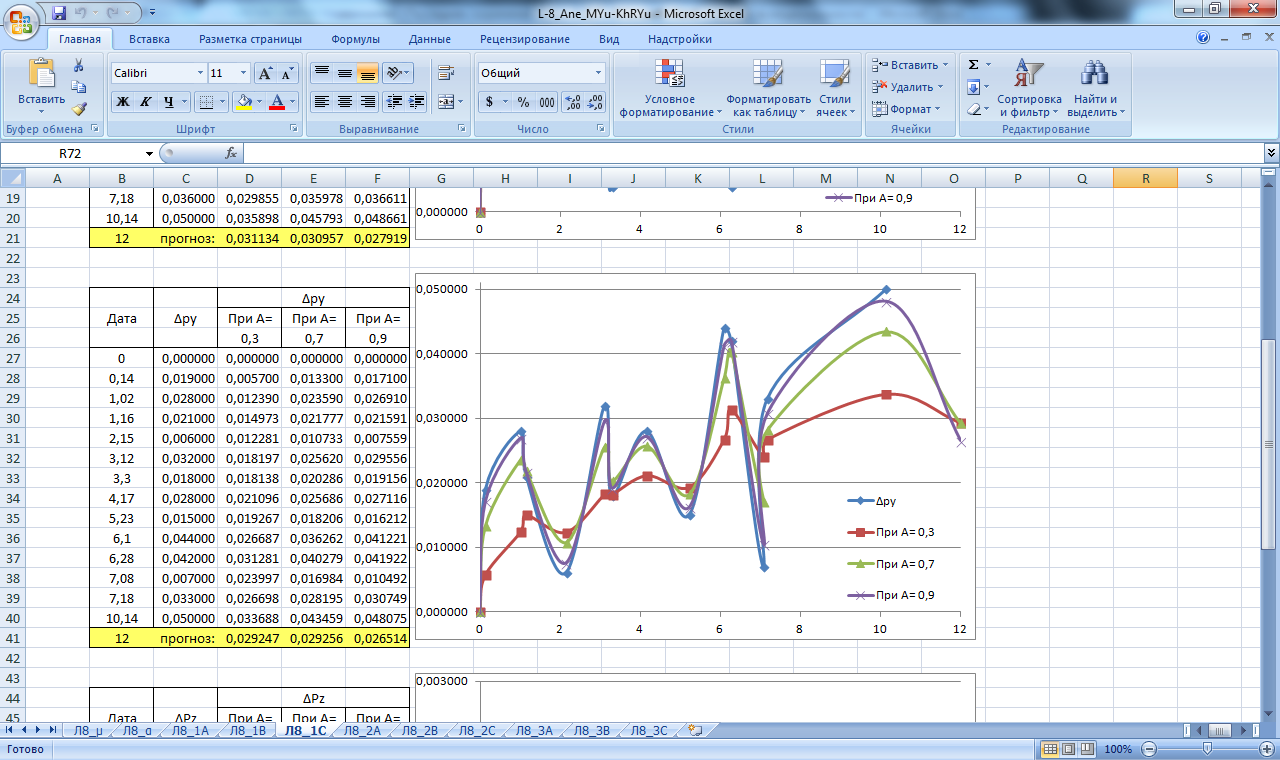
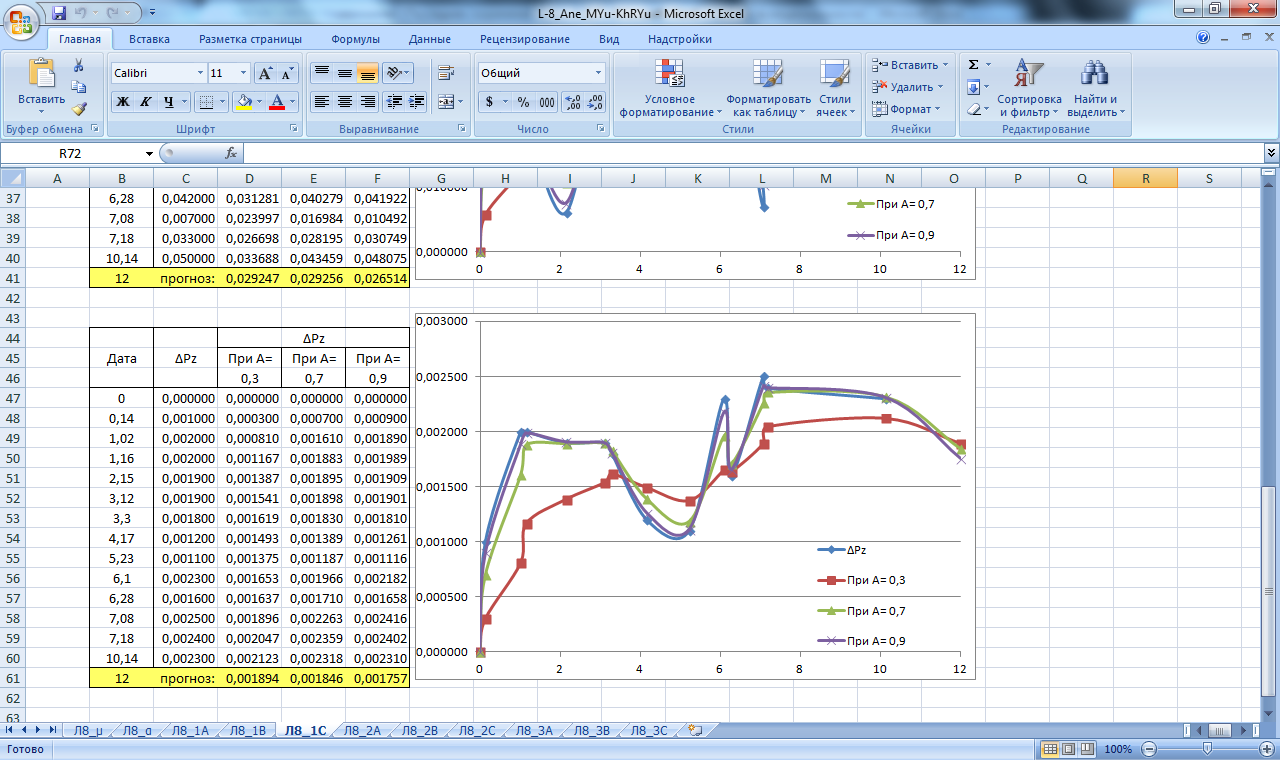
Рисунок 20. Значение сглаживающей функции прогноза смещения в плане и по высоте блока С. Прогнозирование экспоненциальным сглаживанием
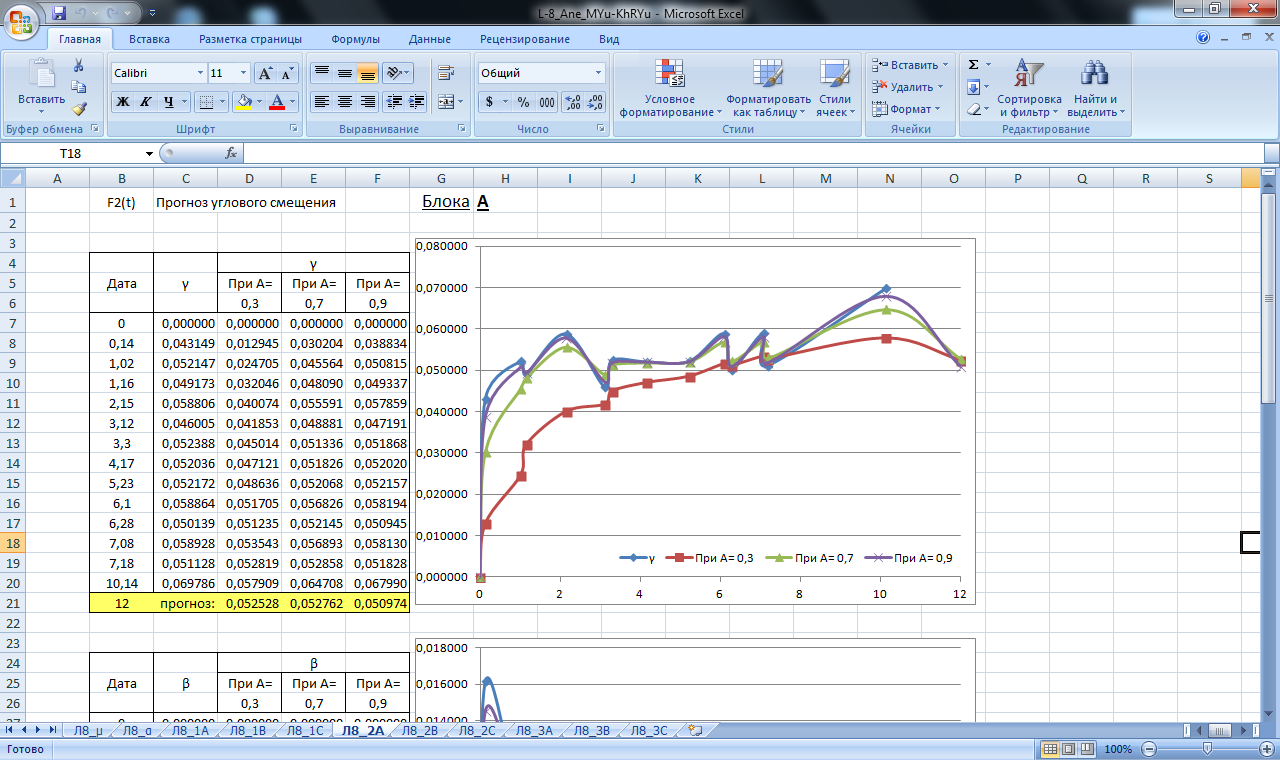
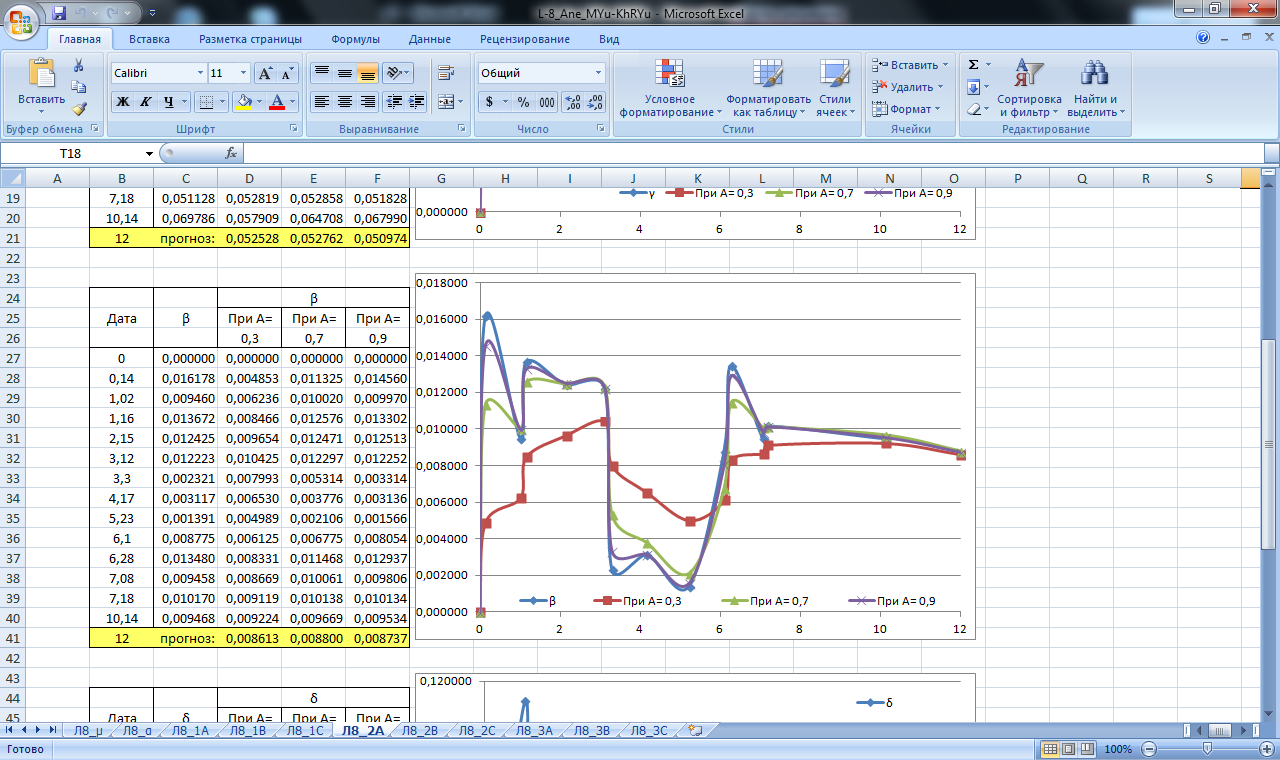
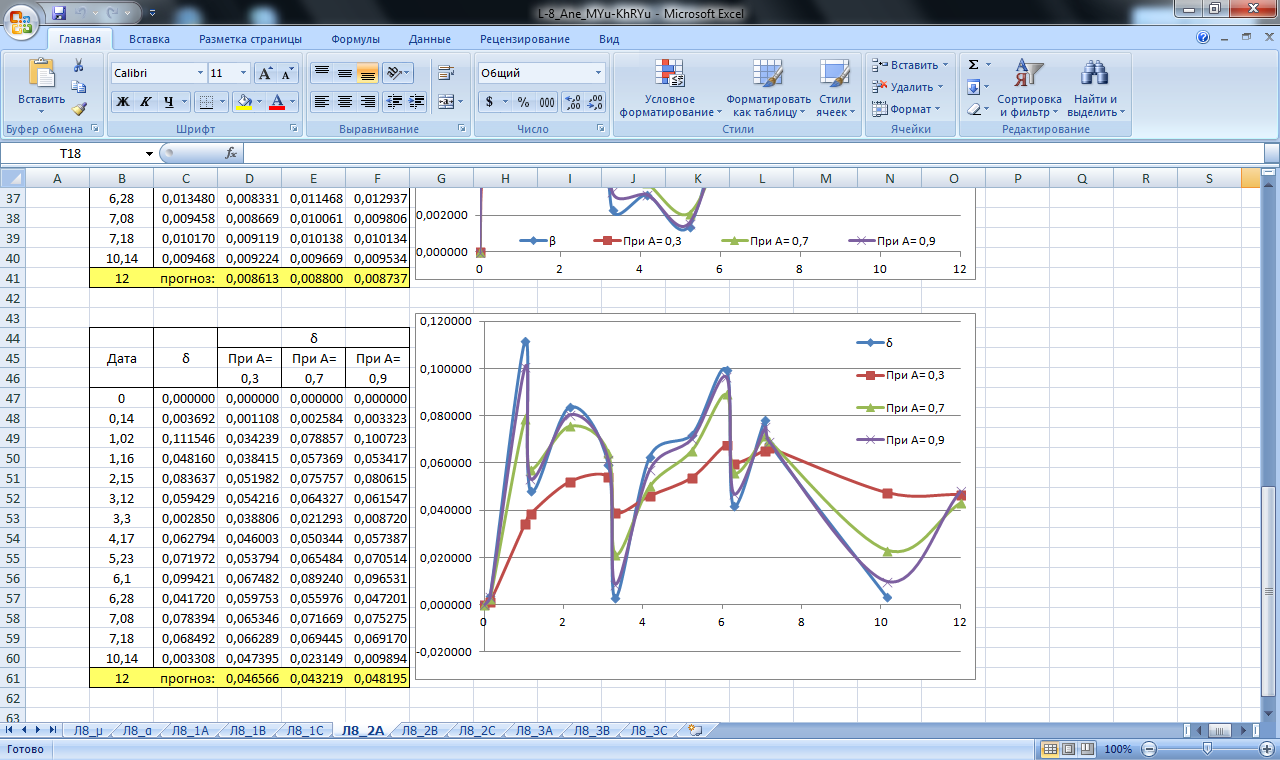
Рисунок 21. Значение сглаживающей функции прогноза углового смещения блока А. Прогнозирование экспоненциальным сглаживанием
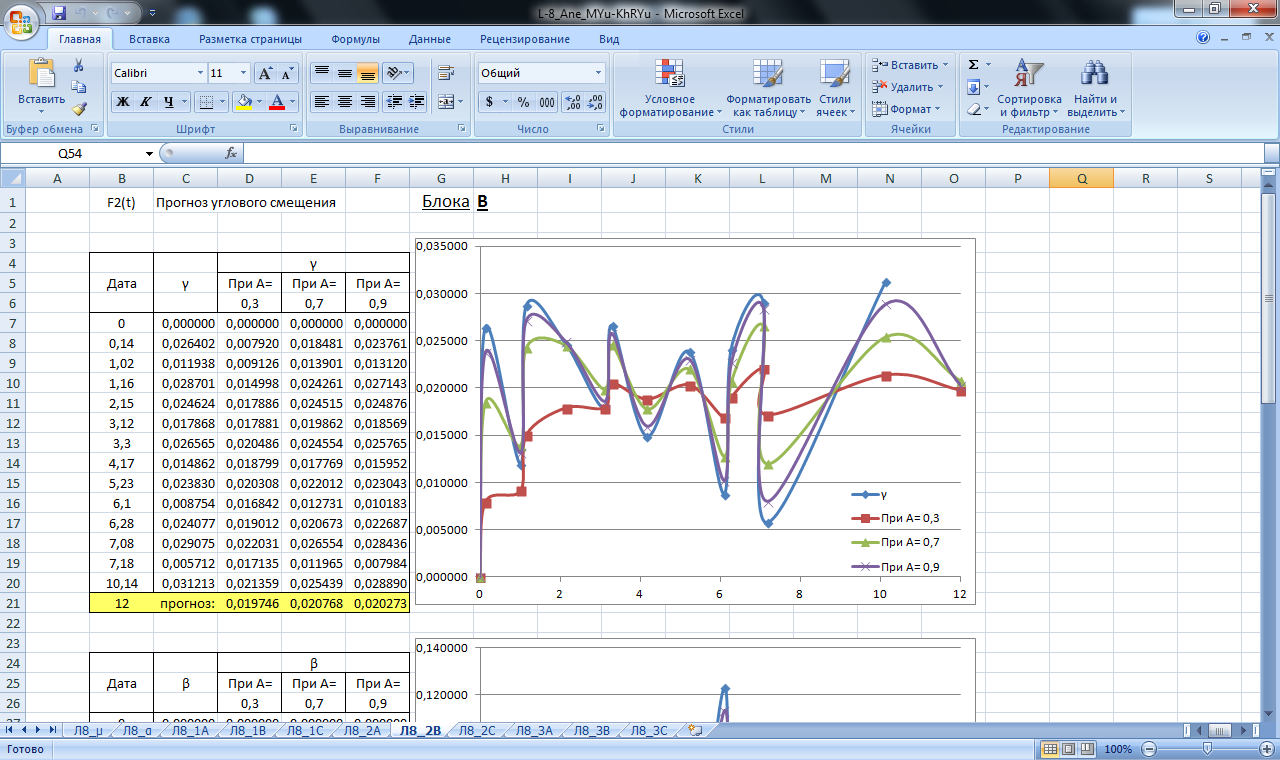
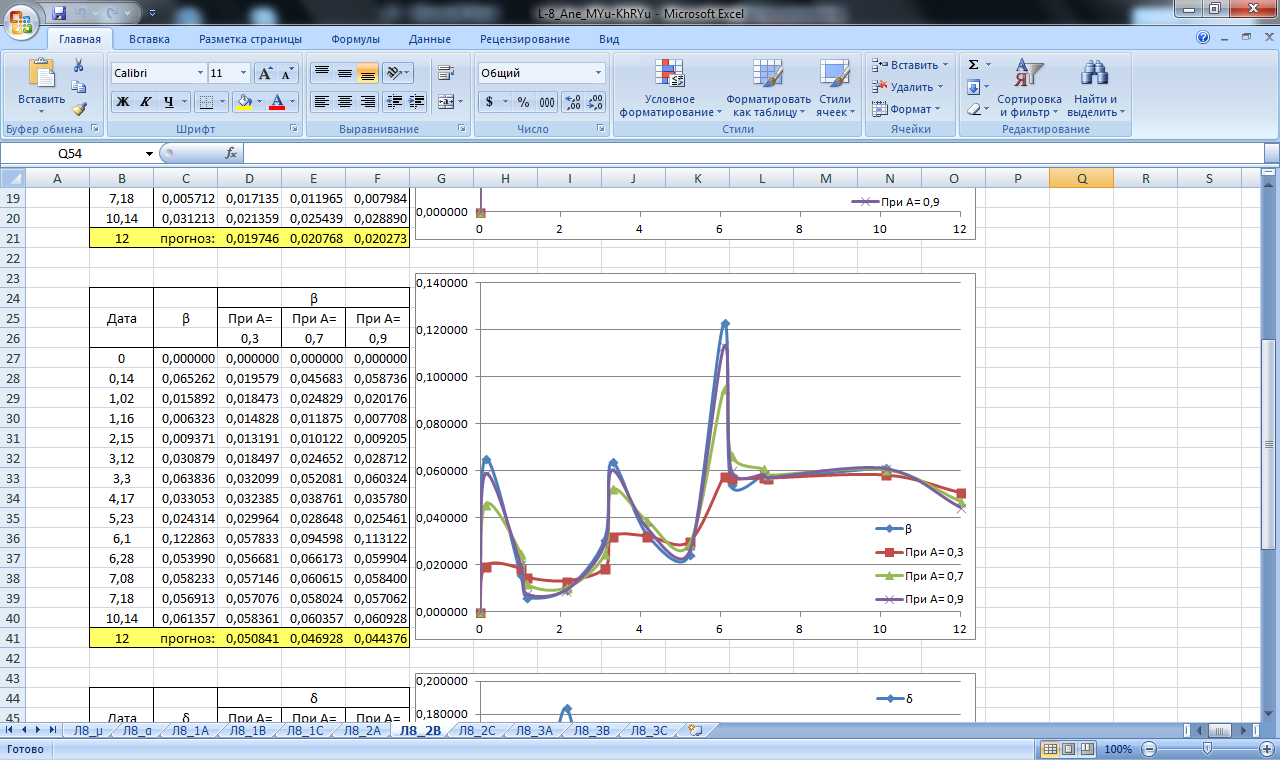
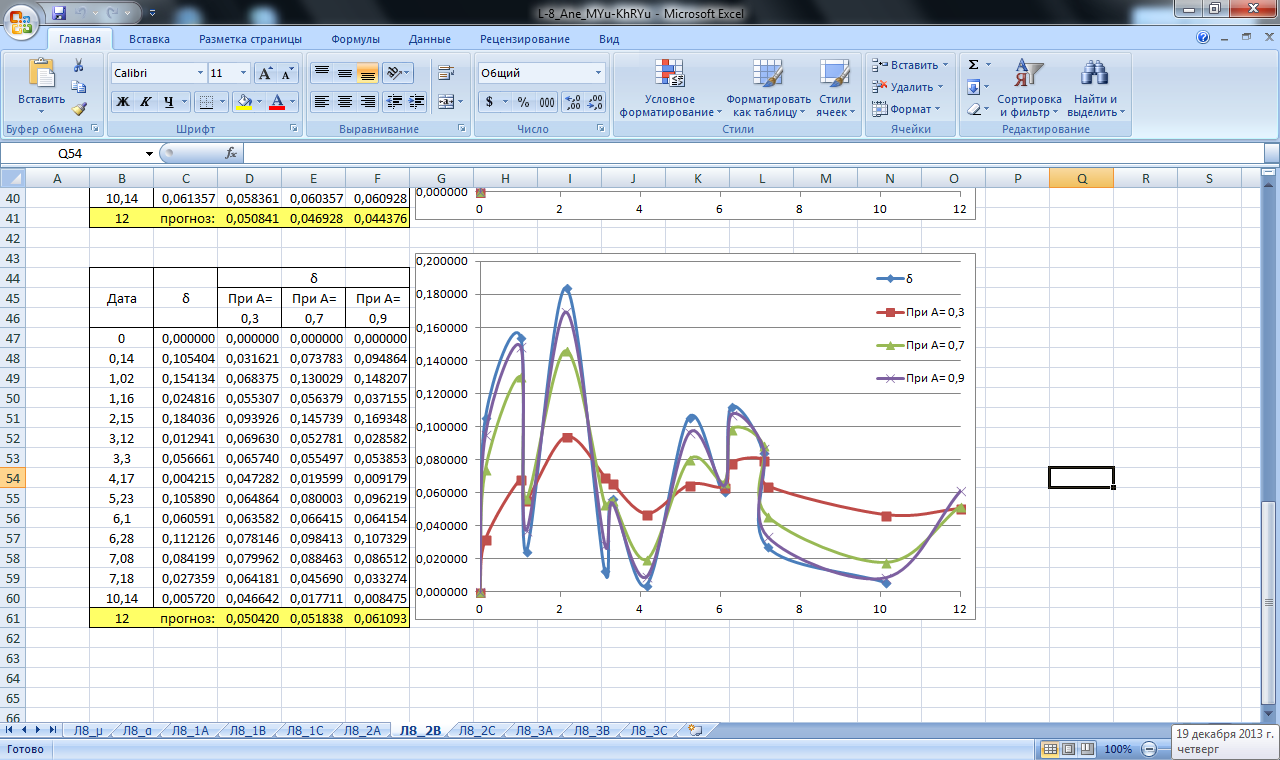
Рисунок 22. Значение сглаживающей функции прогноза углового смещения блока В. Прогнозирование экспоненциальным сглаживанием
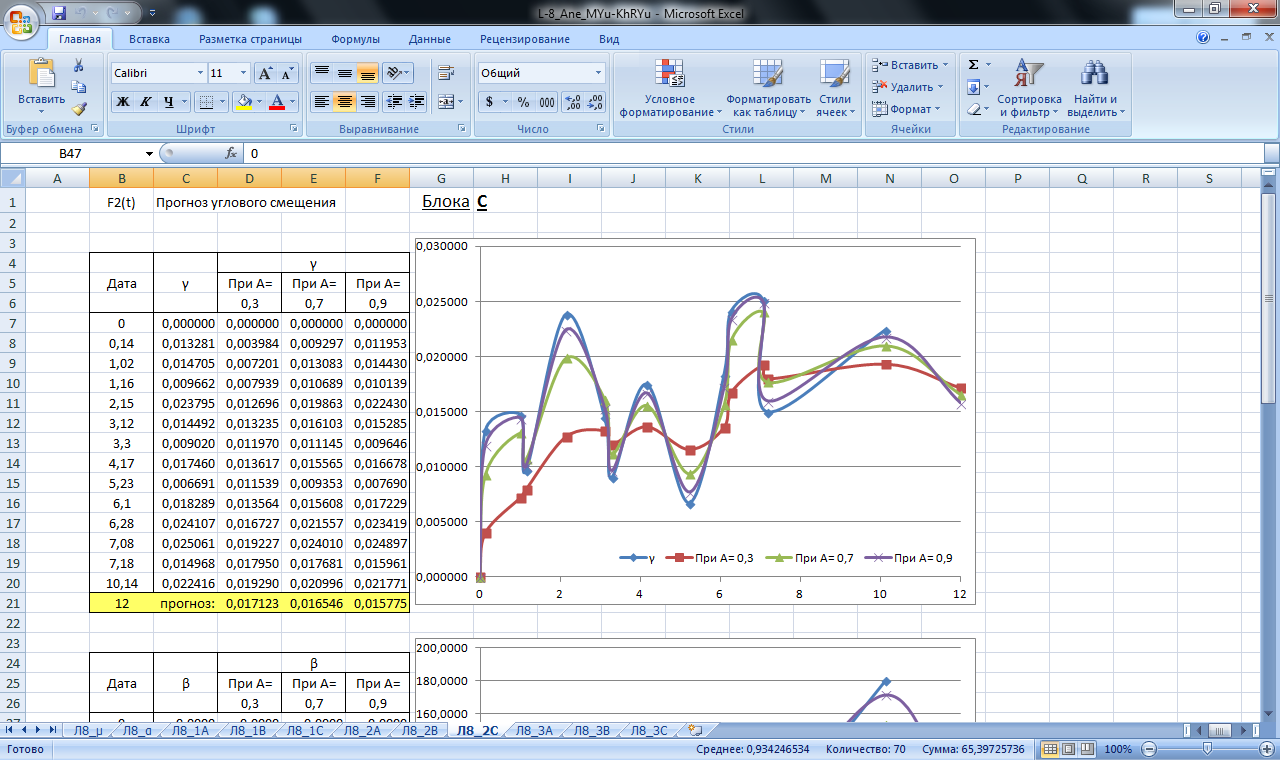
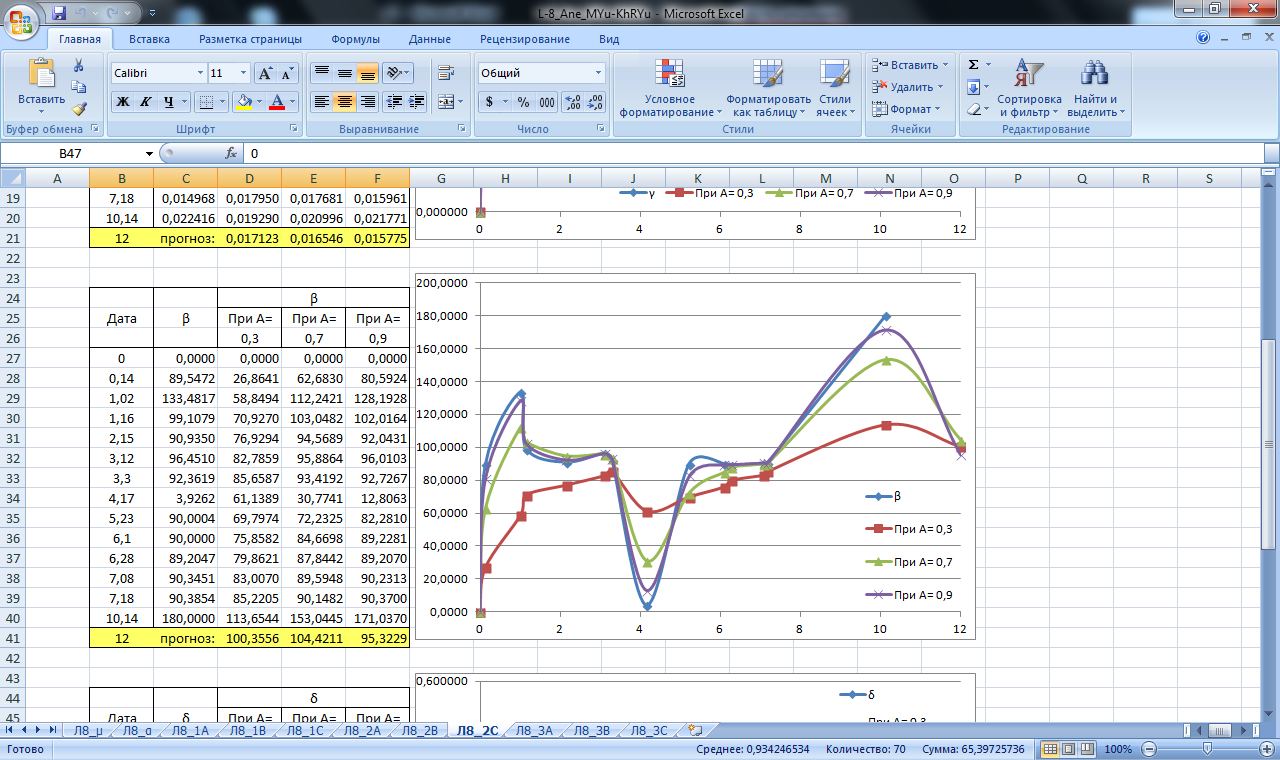
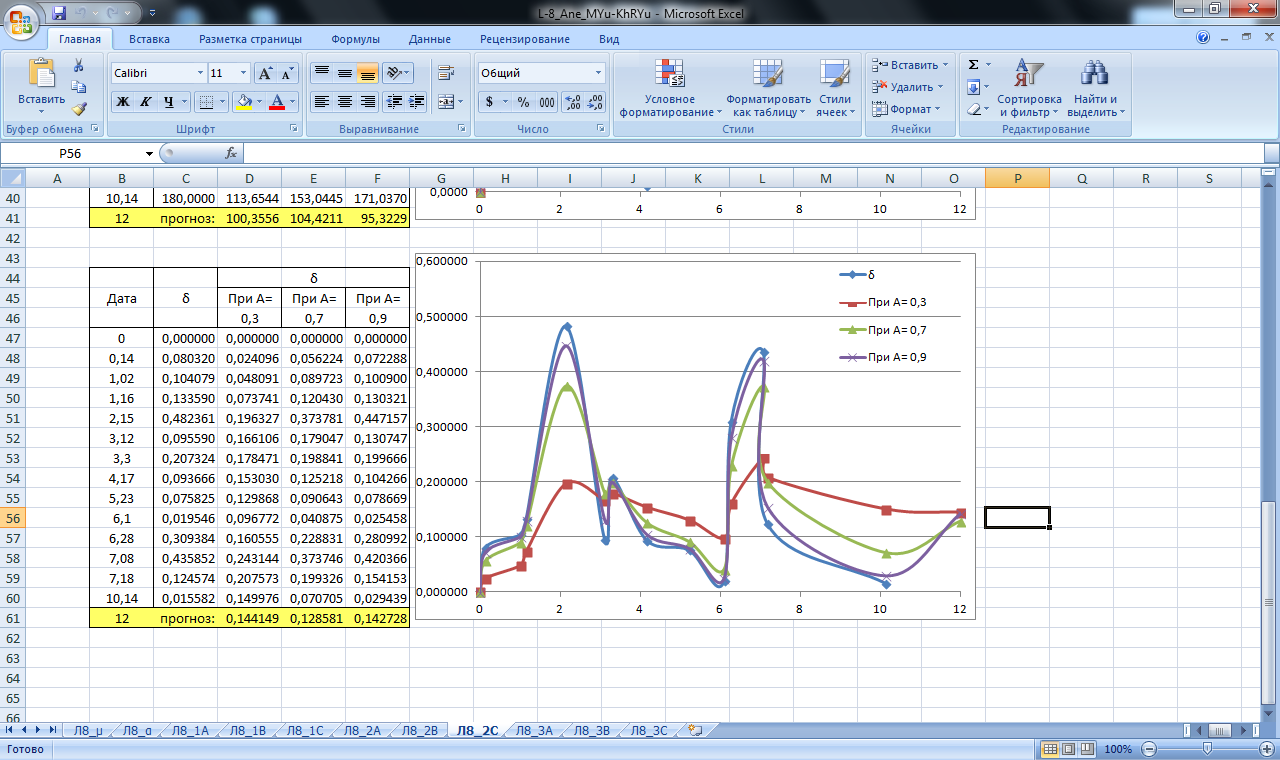
Рисунок 23. Значение сглаживающей функции прогноза углового смещения блока С. Прогнозирование экспоненциальным сглаживанием
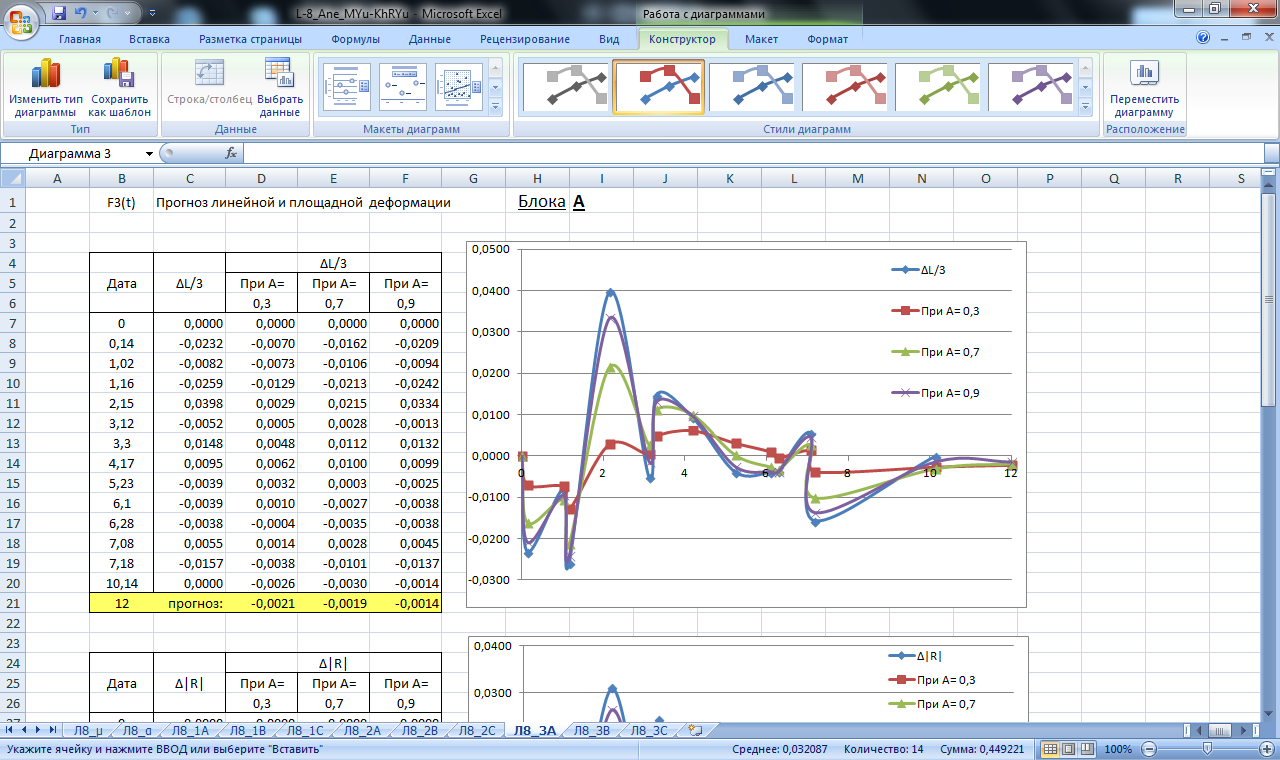
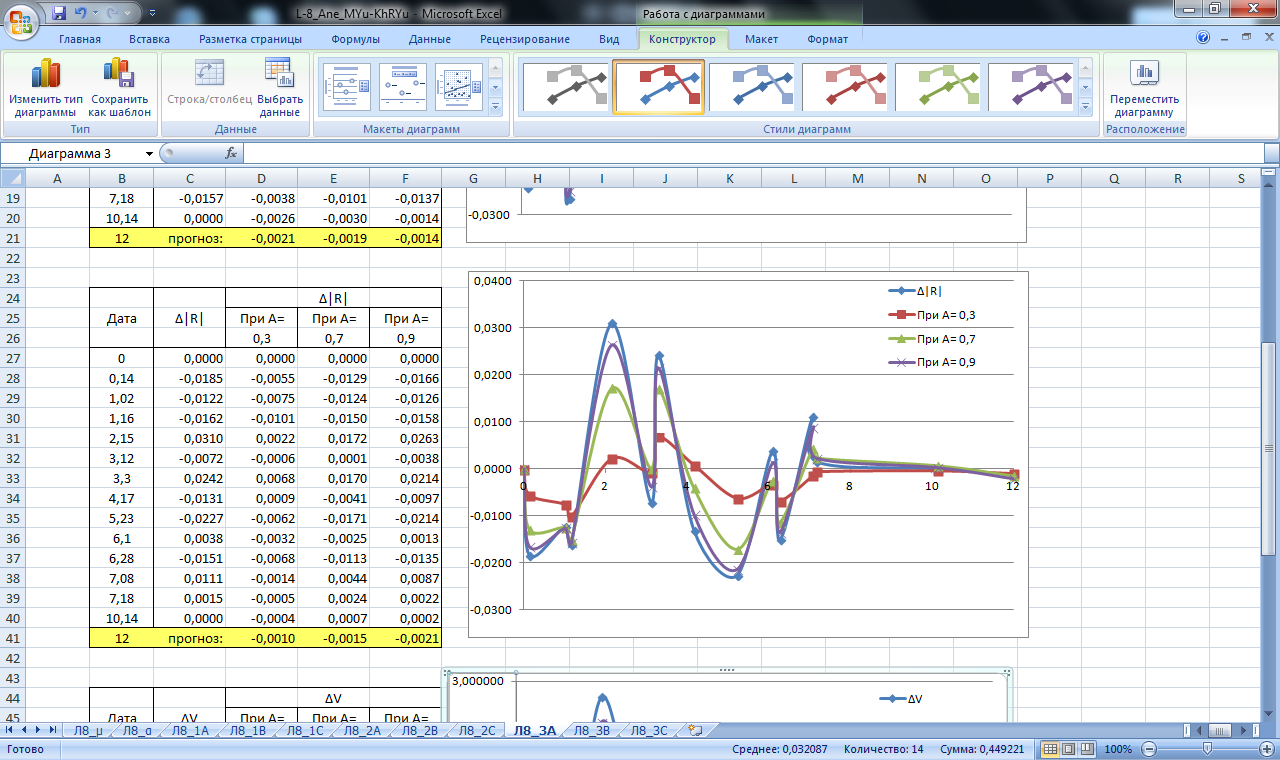
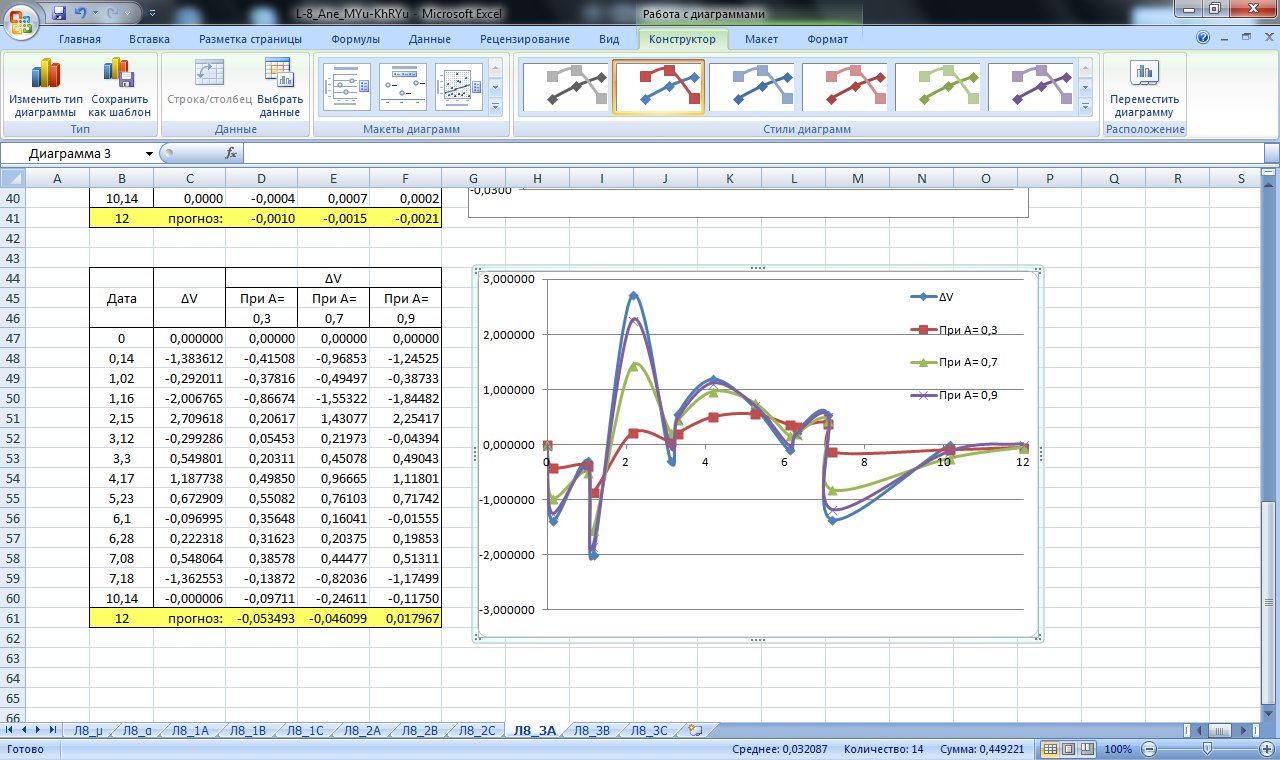
Рисунок 24. Значение сглаживающей функции прогноза линейной и площадной деформации блока А. Прогнозирование экспоненциальным сглаживанием
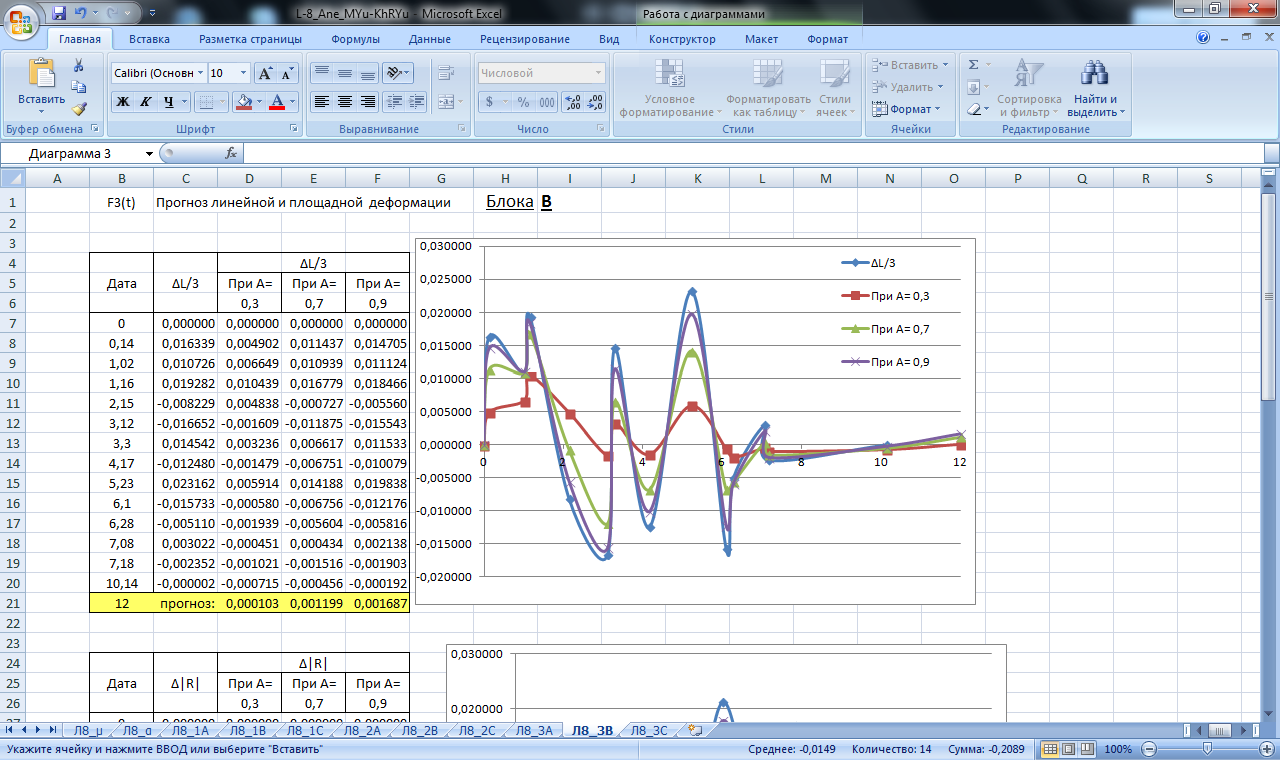
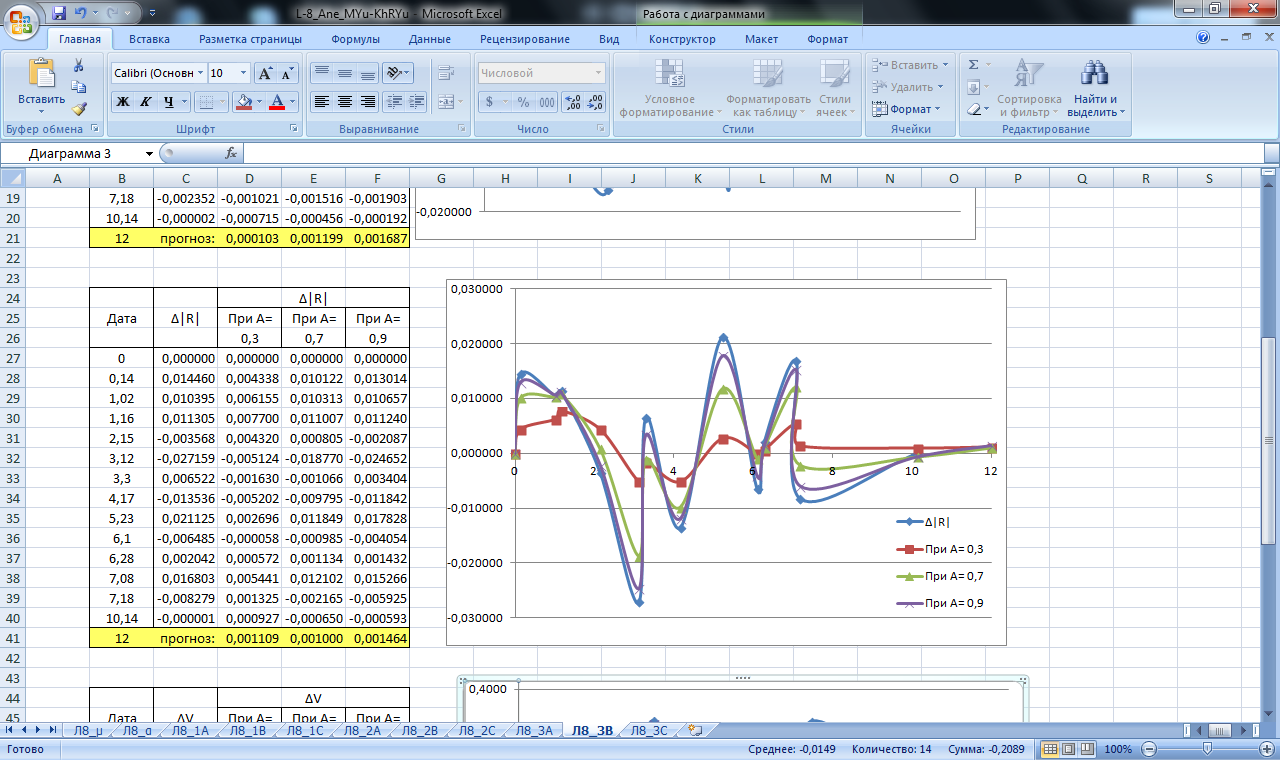
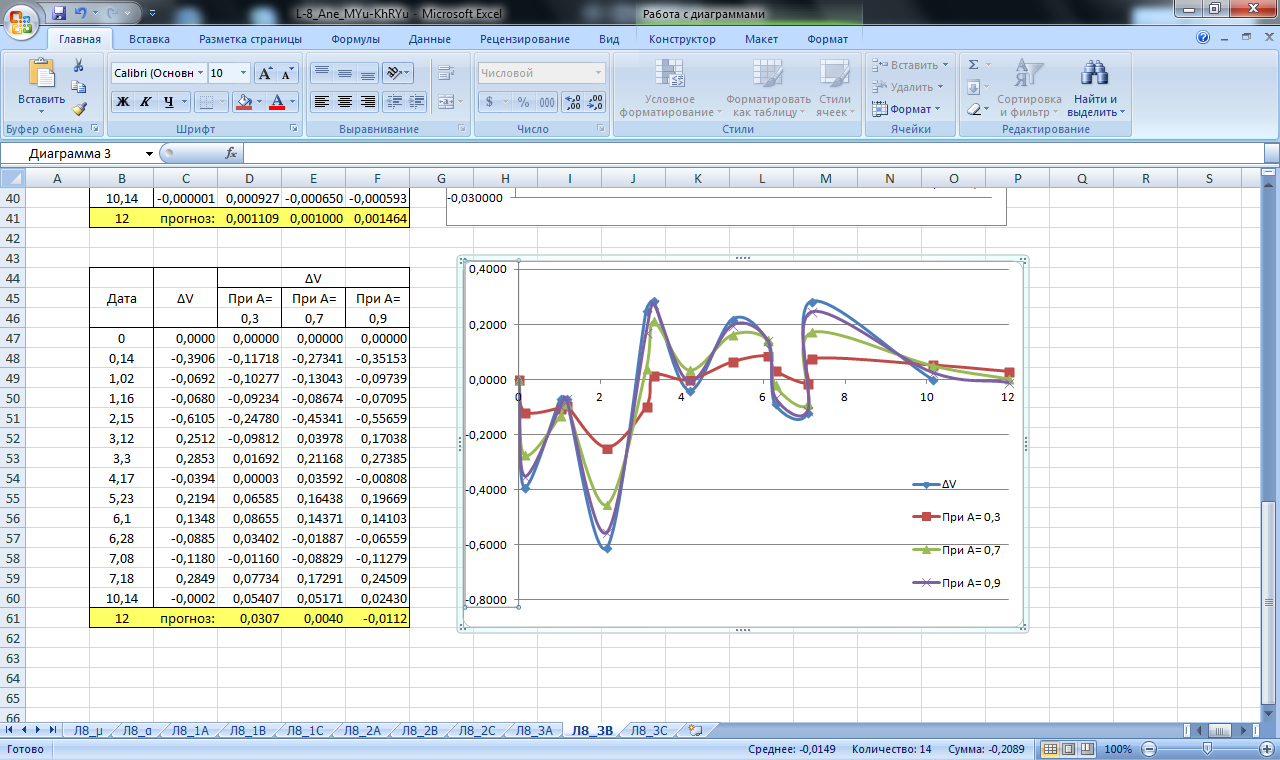
Рисунок 25. Значение сглаживающей функции прогноза линейной и площадной деформации блока В. Прогнозирование экспоненциальным сглаживанием
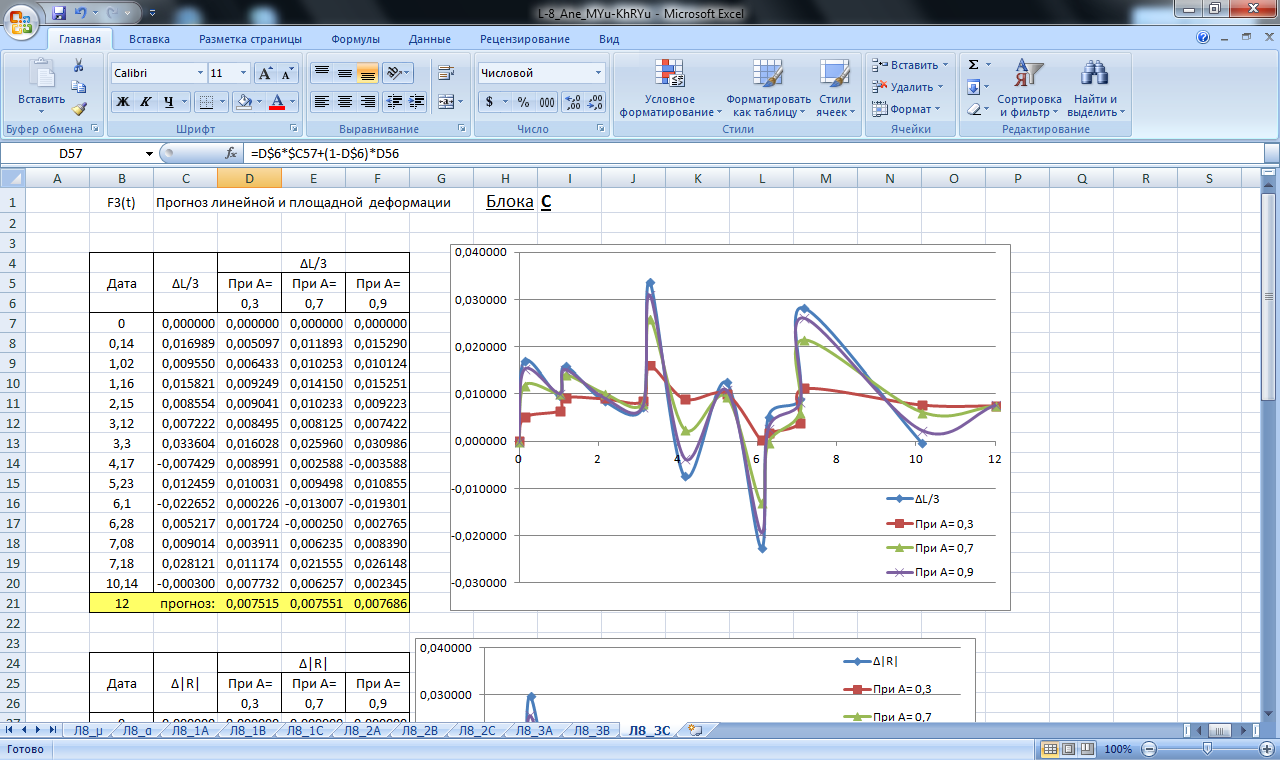
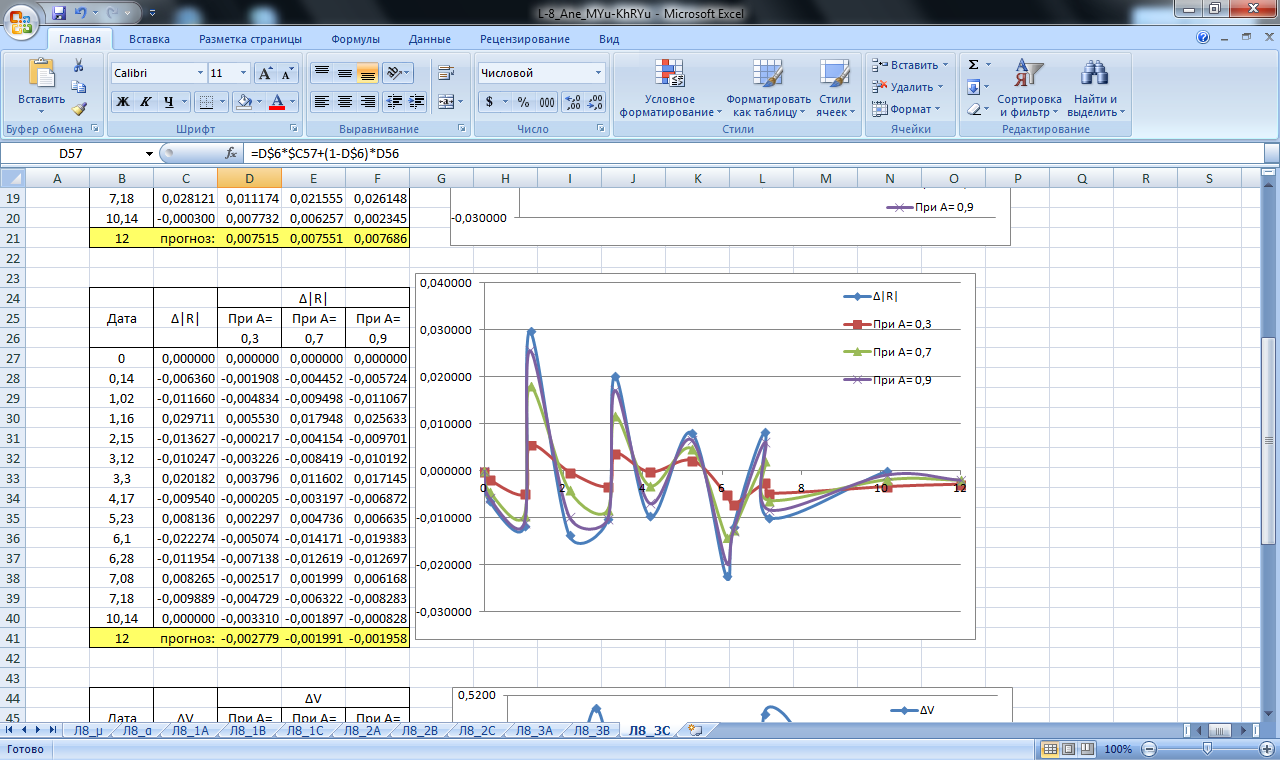
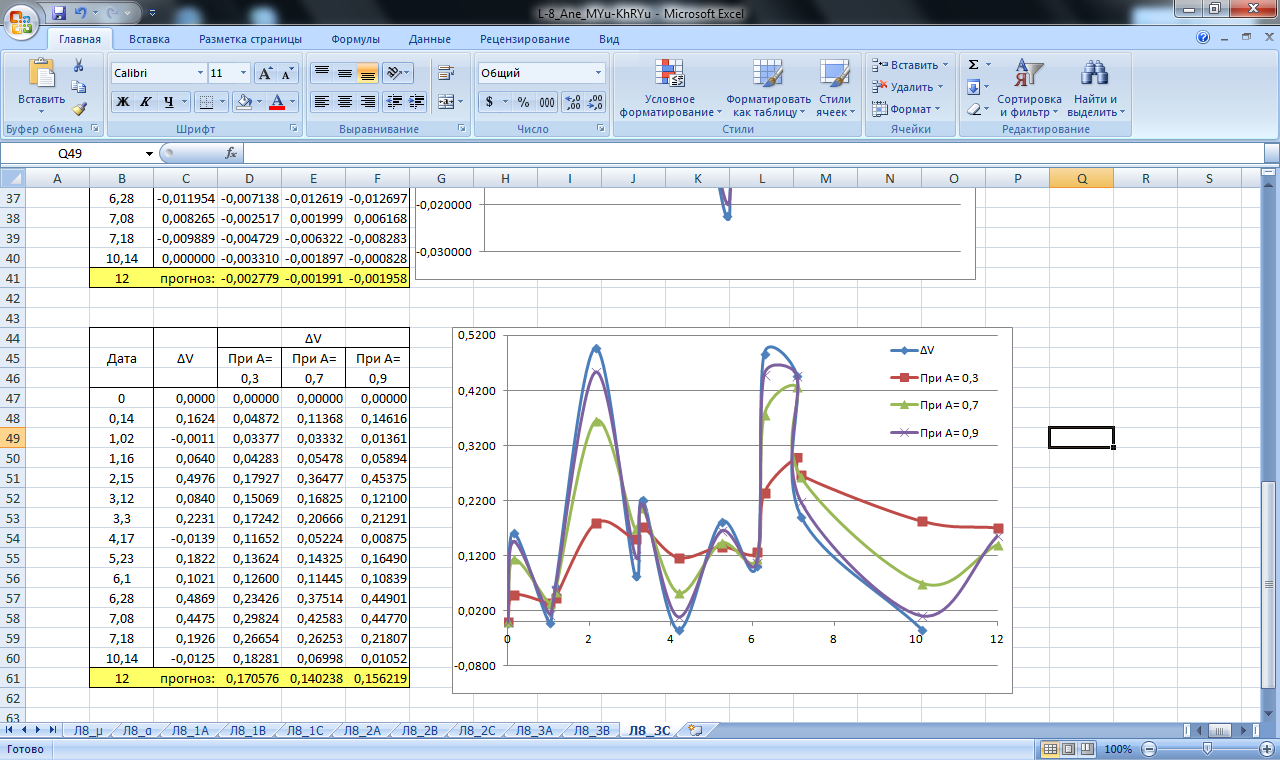
Рисунок 26. Значение сглаживающей функции прогноза линейной и площадной деформации блока С. Прогнозирование экспоненциальным сглаживанием
Таблица 16. Прогнозные значения устойчивости объекта.
|
Блок А |
Блок В |
Блок С |
||||||
Дата |
Вращательное |
Поступательное |
Деформационное |
Вращательное |
Поступательное |
Деформационное |
Вращательное |
Поступательное |
Деформационное |
0 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
0,14 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
1,02 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
1,16 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
2,15 |
+ |
- |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
3,12 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
3,3 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
4,17 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
5,23 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
6,1 |
+ |
- |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
6,28 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
7,08 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
7,18 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
10,14 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
прогноз |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
По полученным результатам можно сделать выводы, что на прогнозные значения ожидается устойчивое стабильное состояние. Критических изменений объекта не прогнозируется.
Независимо от того, что коэффициенты сглаживания от близких к 0 до близких к 1, все три прогнозных функции надежно прогнозируют параметры на следующий временной промежуток.