5.II уровень декомпозиции.
5.1 Определение пространственно-геометрических характеристик объекта. Построение математической модели пространственно-временного состояния объекта.
Блок А
Блок В
Блок С
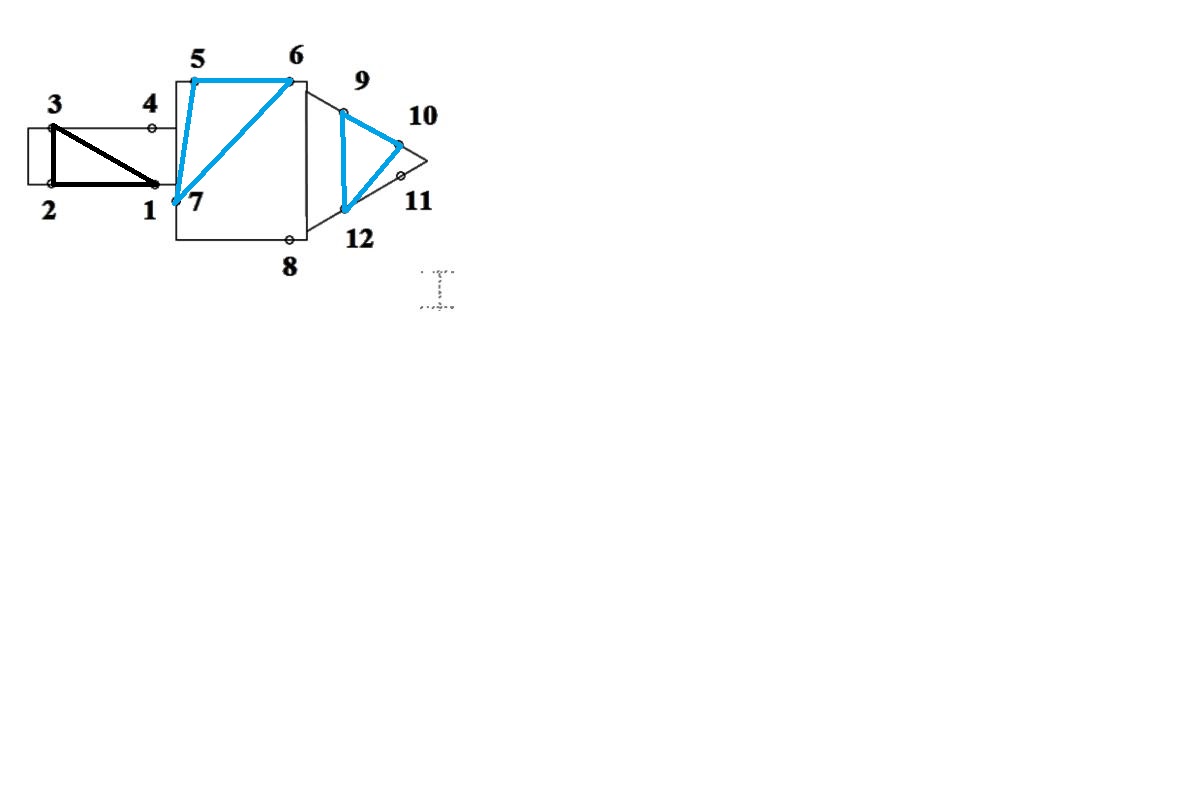
Рисунок 14. Расположение треугольников по блокам.
В предыдущем пункте рассматривалась эволюция состояний объекта, представленного системой точек. Приведенная модель эволюции дает представление о тенденции развития процессов движения и деформации системы в целом. Конструктивные особенности рассматриваемого сооружения свидетельствуют о том, что объект имеет сложную структуру, а значит должен обладать сложными свойствами. Поэтому необходимо рассмотреть не только эволюцию состояний всего объекта, но и эволюцию частей (блоков) объекта.
Применение системного анализа для изучения эволюции состояний объектов позволяет рассматривать тенденцию развития эволюции для разных частей (подсистем) объекта по отношению друг к другу.
Представим систему геодезических точек объекта в виде нескольких подсистем. Общее количество геодезических точек равно 12. Так как объект состоит из 3 блоков, то все точки распределяем равномерно на каждый блок. На каждом блоке будет по 4 точки.
Каждый треугольник изображенный на рисунке 14 позиционируется с соответствующим блоком.
Изучение движений и деформаций техногенных объектов является одной из важнейших задач прикладной геодезии. Контролируемыми параметрами (диагностическими признаками) объектов, для которых используются геодезические методы и средства измерений, являются геометрические величины, характеризующие общие перемещения, положение структурных частей объекта в пространстве и между собой, деформации элементов. К ним относятся осадки, горизонтальные смещения, отклонения от вертикали, прогибы и т.д.
Таким образом, движение любого объекта, наблюдаемого геодезическими методами, складывается из поступательного, вращательного движения и деформационных характеристик.
По результатам повторных геодезических измерений регистрируются изменения координат геодезических точек:
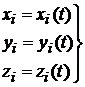(14)
где i – номер геодезической контрольной точки.
Множество точек можно представить в виде совокупности треугольных элементов с вершинами в этих точках (принцип построения триангуляционной сети). Координатами вершин являются координаты контрольных точек (6). Каждый треугольный элемент условно будем считать плоским, а его стороны обозначим векторами, имеющими общее начало.
Плоскость, образованная векторами r1 b r2 определяется уравнением
(15)
Свободный член D есть расстояние s=|V| от начала координат до плоскости. Разности длин проекций |V| на оси x,y,z
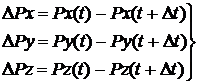(16)
где 
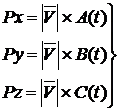(17)
Параметры определяют поступательное движение треугольного элемента относительно системы x,y,z.
Вращательное движение плоскости треугольника характеризуется сочетанием трех составляющих:
- угла поворота γ радиус-вектора относительно вертикальной оси OZ ;
- угла поворота β вектора нормали плоского треугольного элемента;
- угла поворота δ вектора относительно вектора нормали .
Для выявления деформационных характеристик необходимо учесть такие параметры, которые являлись бы инвариантными относительно системы координат. Например, длину вектора , угол , площадь треугольника .
Все перечисленные параметры являются геометрическими свойствами объекта и характеризуют его состояние (геометрическое положение) в пространстве.
Так как движение тела относительно некоторой системы отсчета X Y Z представляет собой совокупность поступательного, вращательного движения и деформации, то изменение состояния объекта во времени и пространстве определится функциями
(18)
(19)
(20)
Нормируя значения аргументов функций (10),(11) и (12) получим пространство состояний (фазовое пространство), где являются явными функциями координат и времени и представляют собой фазовые траектории, характеризующие изменение состояния объекта.
Определение функции f1(ΔPx, ΔPy, ΔPz) где ΔPx, ΔPy, ΔPz- параметры определяющие поступательное движение треугольного элемента относительно системы x,y,z.
ΔPx=хi-x1 (21)
ΔPy=yi-y1 (22)
ΔPz=zi-z1 (23)
По формулам (21-23) рассчитаем параметры поступательного движения, которые приведены в таблице 13.
Таблица 13. Параметры поступательного движения.
Блок А |
|
||||||||||||
Дата |
x |
y |
z |
ΔPx |
ΔPy |
ΔPz |
|
||||||
0 |
20,00 |
21,00 |
29,2222 |
0,00000 |
0,00000 |
0,00000 |
|
||||||
0,14 |
20,02 |
21,04 |
29,2222 |
0,01600 |
0,03800 |
0,00000 |
|
||||||
1,02 |
20,01 |
21,05 |
29,2222 |
0,00500 |
0,04500 |
0,00000 |
|
||||||
1,16 |
20,02 |
21,04 |
29,2226 |
0,02200 |
0,04300 |
0,00040 |
|
||||||
2,15 |
20,05 |
21,04 |
29,2227 |
0,04600 |
0,03800 |
0,00050 |
|
||||||
3,12 |
20,02 |
21,04 |
29,2228 |
0,01700 |
0,04100 |
0,00060 |
|
||||||
3,3 |
20,04 |
21,04 |
29,2222 |
0,03600 |
0,03900 |
0,00000 |
|
||||||
4,17 |
20,03 |
21,04 |
29,2222 |
0,02700 |
0,04400 |
0,00000 |
|
||||||
5,23 |
20,00 |
21,05 |
29,2226 |
0,00400 |
0,04500 |
0,00040 |
|
||||||
6,1 |
20,04 |
21,04 |
29,2227 |
0,04300 |
0,04200 |
0,00050 |
|
||||||
6,28 |
20,02 |
21,04 |
29,2218 |
0,01700 |
0,04400 |
0,00040 |
|
||||||
7,08 |
20,04 |
21,04 |
29,2226 |
0,04200 |
0,04300 |
0,00040 |
|
||||||
7,18 |
20,01 |
21,05 |
29,2222 |
0,01000 |
0,04500 |
0,00000 |
|
||||||
10,14 |
20,05 |
21,05 |
29,2222 |
0,05000 |
0,05000 |
0,00000 |
|
||||||
Блок Б |
|
||||||||||||
Дата |
x |
y |
h |
ΔPx |
Δpy |
ΔPz |
|
||||||
0 |
40,00 |
35,50 |
29,2222 |
0,0000 |
0,0000 |
0,0000 |
|
||||||
0,14 |
40,04 |
35,51 |
29,2222 |
0,0420 |
0,0080 |
0,0000 |
|
||||||
1,02 |
40,02 |
35,51 |
29,2224 |
0,0210 |
0,0080 |
0,0002 |
|
||||||
1,16 |
40,03 |
35,55 |
29,2222 |
0,0300 |
0,0480 |
0,0000 |
|
||||||
2,15 |
40,01 |
35,54 |
29,2224 |
0,0070 |
0,0360 |
0,0002 |
|
||||||
3,12 |
40,01 |
35,53 |
29,2222 |
0,0050 |
0,0260 |
0,0000 |
|
||||||
3,3 |
40,02 |
35,54 |
29,2222 |
0,0240 |
0,0440 |
0,0000 |
|
||||||
4,17 |
40,01 |
35,52 |
29,2224 |
0,0100 |
0,0240 |
0,0002 |
|
||||||
5,23 |
40,04 |
35,53 |
29,2222 |
0,0420 |
0,0310 |
0,0000 |
|
||||||
6,1 |
40,02 |
35,51 |
29,2234 |
0,0160 |
0,0050 |
0,0012 |
|
||||||
6,28 |
40,04 |
35,54 |
29,2232 |
0,0400 |
0,0380 |
0,0010 |
|
||||||
7,08 |
40,05 |
35,55 |
29,2234 |
0,0450 |
0,0480 |
0,0012 |
|
||||||
7,18 |
40,01 |
35,51 |
29,2234 |
0,0110 |
0,0100 |
0,0012 |
|
||||||
10,14 |
40,05 |
35,55 |
29,2232 |
0,0500 |
0,0500 |
0,0010 |
|
||||||
Блок С |
|||||||||||||
Дата |
x |
y |
h |
ΔPx |
Δpy |
ΔPz |
|||||||
0 |
45,00 |
45,00 |
29,2311 |
0,0000 |
0,0000 |
0,0000 |
|||||||
0,14 |
45,03 |
45,02 |
29,2321 |
0,0310 |
0,0190 |
0,0010 |
|||||||
1,02 |
45,04 |
45,03 |
29,2331 |
0,0360 |
0,0280 |
0,0020 |
|||||||
1,16 |
45,01 |
45,02 |
29,2331 |
0,0070 |
0,0210 |
0,0020 |
|||||||
2,15 |
45,04 |
45,01 |
29,233 |
0,0430 |
0,0060 |
0,0019 |
|||||||
3,12 |
45,01 |
45,03 |
29,233 |
0,0130 |
0,0320 |
0,0019 |
|||||||
3,3 |
45,00 |
45,02 |
29,2329 |
0,0040 |
0,0180 |
0,0018 |
|||||||
4,17 |
45,04 |
45,03 |
29,2323 |
0,0410 |
0,0280 |
0,0012 |
|||||||
5,23 |
45,02 |
45,02 |
29,2322 |
0,0160 |
0,0150 |
0,0011 |
|||||||
6,1 |
45,04 |
45,04 |
29,2334 |
0,0370 |
0,0440 |
0,0023 |
|||||||
6,28 |
45,00 |
45,04 |
29,2327 |
0,0040 |
0,0420 |
0,0016 |
|||||||
7,08 |
45,05 |
45,01 |
29,2336 |
0,0460 |
0,0070 |
0,0025 |
|||||||
7,18 |
45,04 |
45,03 |
29,2335 |
0,0360 |
0,0330 |
0,0024 |
|||||||
10,14 |
45,05 |
45,05 |
29,2334 |
0,0500 |
0,0500 |
0,0023 |
|||||||
На основании данных таблицы 13 построен график траектории функции f1(ΔPx, ΔPy, ΔPz) представленный на рисунке 15.
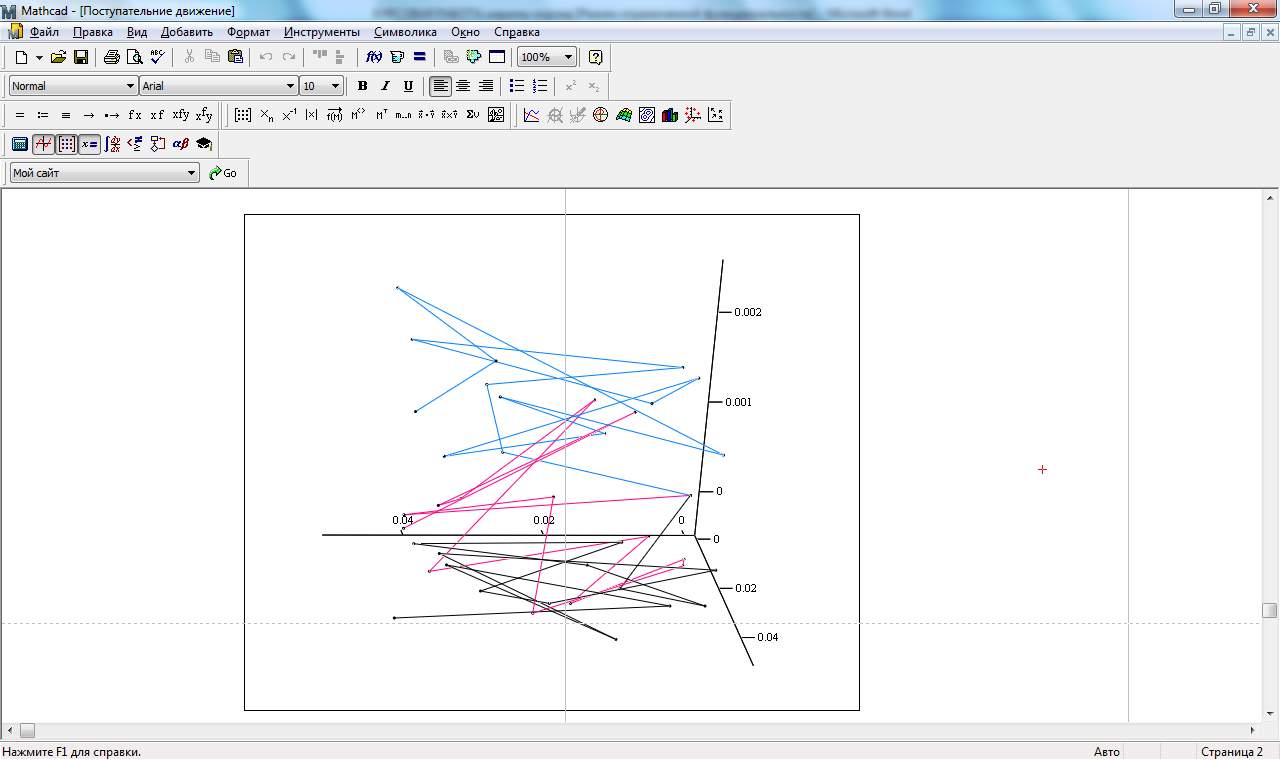
Блок А ___
Блок В ___
Блок С ___
Рисунок 15. Траектории функции f1(ΔPx, ΔPy, ΔPz)
Определение функции f2(γ, β, δ) где
-угла поворота γ радиус-вектора относительно вертикальной оси OZ ;
- угла поворота β вектора нормали плоского треугольного элемента;
- угла поворота δ вектора относительно вектора нормали .
(24)
(25)
Координатные формулы
(26) |
(27) |
|
(28) |
(29) |
|
|
|
(30) |
|
(31) |
(32) |
-
взаимно ортогональные единичные векторы,
имеющие направления координатных осей;
или 
Тогда: 
По формулам (24-32) рассчитаем параметры вращательного движения, которые приведены в таблице 14.
Таблица14 . Параметры вращательного движения
Блок А(1,2,3) |
Блок B(6,5,8) |
Блок C (9,11,12) |
|||||||||
Дата |
γ |
β |
δ |
Дата |
γ |
β |
δ |
Дата |
γ |
β |
δ |
0 |
0,0000 |
0,0000 |
0,0000 |
0 |
0,0000 |
0,0000 |
0,0000 |
0 |
0,0000 |
0,0000 |
0,0000 |
0,14 |
0,0431 |
0,0000 |
0,0037 |
0,14 |
0,0264 |
0,0197 |
0,0754 |
0,14 |
0,0133 |
0,4867 |
0,0664 |
1,02 |
0,0521 |
0,0535 |
0,1115 |
1,02 |
0,0119 |
0,0535 |
0,0362 |
1,02 |
0,0147 |
0,2549 |
0,0370 |
1,16 |
0,0492 |
0,0019 |
0,0482 |
1,16 |
0,0287 |
0,1152 |
0,1225 |
1,16 |
0,0097 |
0,8273 |
0,0577 |
2,15 |
0,0588 |
0,0000 |
0,0836 |
2,15 |
0,0246 |
0,0737 |
0,0865 |
2,15 |
0,0238 |
0,9850 |
0,2074 |
3,12 |
0,0460 |
0,0001 |
0,0594 |
3,12 |
0,0179 |
0,0768 |
0,0324 |
3,12 |
0,0145 |
0,7170 |
0,0425 |
3,3 |
0,0524 |
0,0409 |
0,0029 |
3,3 |
0,0266 |
0,0439 |
0,1563 |
3,3 |
0,0090 |
0,6562 |
0,0117 |
4,17 |
0,0520 |
0,2143 |
0,0628 |
4,17 |
0,0149 |
0,0704 |
0,0831 |
4,17 |
0,0175 |
0,0661 |
0,1084 |
5,23 |
0,0522 |
0,2877 |
0,0720 |
5,23 |
0,0238 |
0,0017 |
0,3107 |
5,23 |
0,0067 |
0,5102 |
0,0685 |
6,1 |
0,0589 |
0,0388 |
0,0994 |
6,1 |
0,0088 |
0,0408 |
0,1581 |
6,1 |
0,0183 |
0,1420 |
0,0517 |
6,28 |
0,0501 |
0,0214 |
0,0417 |
6,28 |
0,0241 |
0,0511 |
0,0876 |
6,28 |
0,0241 |
0,3927 |
0,0863 |
7,08 |
0,0589 |
0,0270 |
0,0784 |
7,08 |
0,0291 |
0,0233 |
0,0618 |
7,08 |
0,0251 |
0,8940 |
0,2207 |
7,18 |
0,0511 |
0,0035 |
0,0685 |
7,18 |
0,0057 |
0,1192 |
0,0226 |
7,18 |
0,0150 |
0,0636 |
0,0187 |
10,14 |
0,0698 |
0,0000 |
0,0033 |
10,14 |
0,0312 |
0,0185 |
0,0007 |
10,14 |
0,0224 |
0,0000 |
0,0100 |
На основании данных таблицы 14 построен график траектории функции f2(γ, β, δ) представленный на рисунке 16.
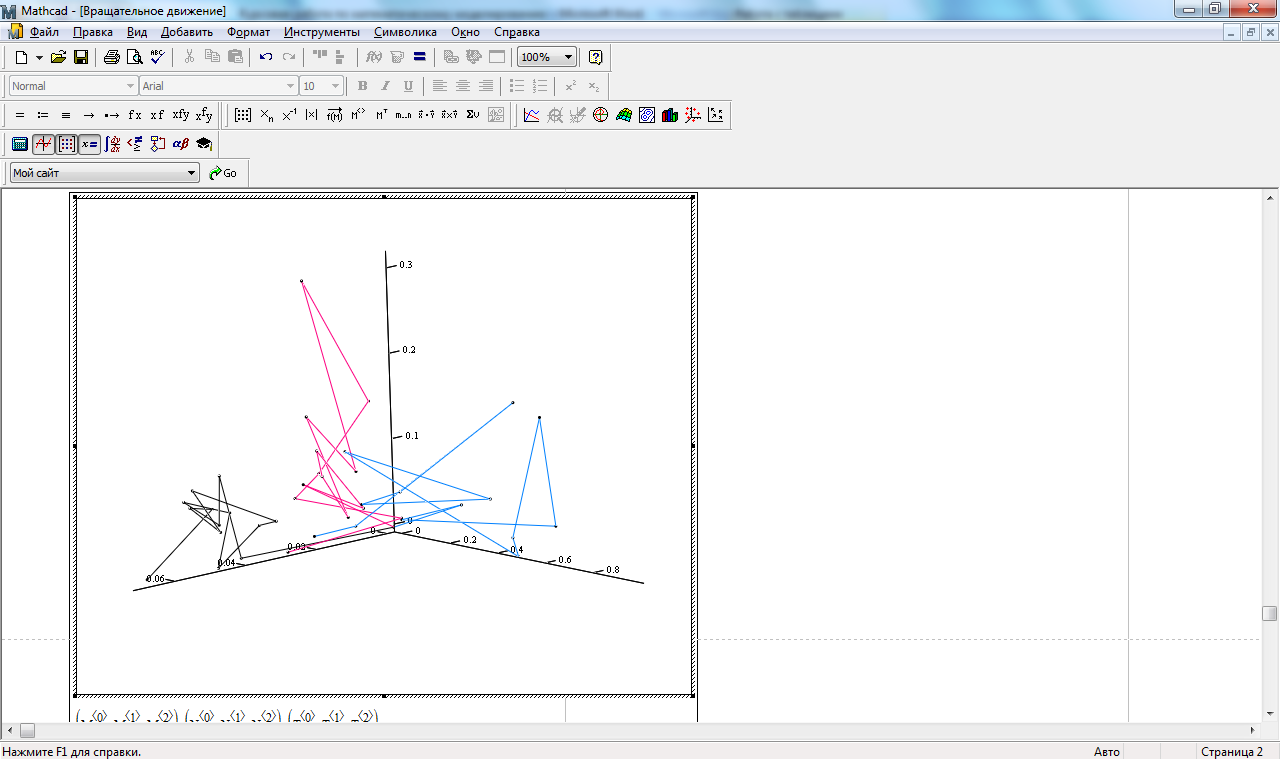
Блок А ___
Блок В ___
Блок С ___
Рисунок 16. Траектории вращательного движения.
Определение функции f3(ΔL/3, Δ|R|, S). Длина стороны L , разница между нулевым и последующим вектором R , площадь треугольника S.
(33)
(34)
По формулам (32-34) рассчитаем параметры поступательного движения, которые приведены в таблице 15.
Таблица 15. Параметры деформационного движения.
|
Блок А |
Блок В |
Блок С |
||||||
Дата |
ΔL/3 |
Δ|R| |
S |
ΔL/3 |
Δ|R| |
S |
ΔL/3 |
Δ|R| |
S |
0 |
0 |
0,0000 |
0,000 |
0,00000 |
0,0000 |
0,000 |
0,00000 |
0,0000 |
0,0000 |
0,14 |
-0,02320 |
-0,0185 |
-1,384 |
0,01634 |
0,0145 |
-0,391 |
0,01699 |
-0,0064 |
0,1624 |
1,02 |
-0,00815 |
-0,0122 |
-0,292 |
0,01073 |
0,0104 |
-0,069 |
0,00955 |
-0,0117 |
-0,0011 |
1,16 |
-0,02585 |
-0,0162 |
-2,007 |
0,01928 |
0,0113 |
-0,068 |
0,01582 |
0,0297 |
0,0640 |
2,15 |
0,03977 |
0,0310 |
2,710 |
-0,00823 |
-0,0036 |
-0,611 |
0,00855 |
-0,0136 |
0,4976 |
3,12 |
-0,00521 |
-0,0072 |
-0,299 |
-0,01665 |
-0,0272 |
0,251 |
0,00722 |
-0,0102 |
0,0840 |
3,3 |
0,01483 |
0,0242 |
0,550 |
0,01454 |
0,0065 |
0,285 |
0,03360 |
0,0202 |
0,2231 |
4,17 |
0,00948 |
-0,0131 |
1,188 |
-0,01248 |
-0,0135 |
-0,039 |
-0,00743 |
-0,0095 |
-0,0139 |
5,23 |
-0,00390 |
-0,0227 |
0,673 |
0,02316 |
0,0211 |
0,219 |
0,01246 |
0,0081 |
0,1822 |
6,1 |
-0,00392 |
0,0038 |
-0,097 |
-0,01573 |
-0,0065 |
0,135 |
-0,02265 |
-0,0223 |
0,1021 |
6,28 |
-0,00379 |
-0,0151 |
0,222 |
-0,00511 |
0,0020 |
-0,089 |
0,00522 |
-0,0120 |
0,4869 |
7,08 |
0,00547 |
0,0111 |
0,548 |
0,00302 |
0,0168 |
-0,118 |
0,00901 |
0,0083 |
0,4475 |
7,18 |
-0,01570 |
0,0015 |
-1,363 |
-0,00235 |
-0,0083 |
0,285 |
0,02812 |
-0,0099 |
0,1926 |
10,14 |
0,000021 |
0,00013 |
0,00001 |
0,00003 |
0,00012 |
0,001 |
-0,00030 |
0,0000 |
-0,0125 |
На основании данных таблицы 15 построен график траектории функции f3(ΔL/3, Δ|R|, S) представленный на рисунке 17.
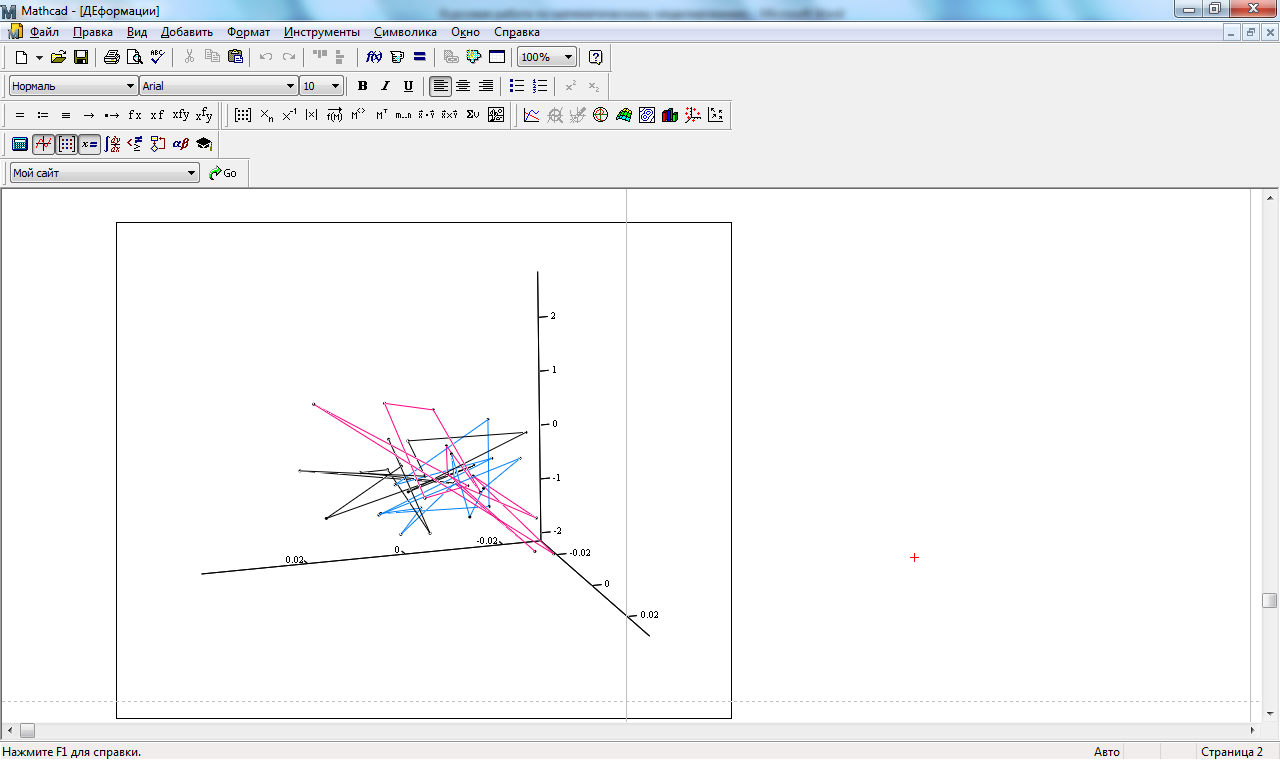
Блок А ___
Блок В ___
Блок С ___
Рисунок 17. Траектория деформационного движения.
Вывод: построены графики траекторий поступательного, вращательного и деформационного движений для каждого треугольного элемента.