4.2 Прогнозирование функции отклика объекта на изменение его геометрических свойств.
Движение в пространстве и времени есть функция отклика объекта в результате какого-то внешнего воздействия, т.е. функция представляет реакцию объекта на это воздействие. В нашем случае функцией отклика будет являться фазовая траектория.
Любую функцию можно прогнозировать различными методами:
Эвристический метод основан на мнении высококвалифицированных специалистов в данной области знания, что дает возможность избежать грубых ошибок, особенно в области скачкообразных изменений прогнозируемой величины. Метод эвристического прогнозирования в основном используется для прогнозирования процессов, формализацию которых нельзя привести к моменту прогнозирования.
Математическое прогнозирование заключается в использовании имеющихся (до определенного времени) данных о некоторых характеристиках прогнозируемого объекта, обработке этих данных математическими методами и определении функций зависимости этих характеристик от времени (или от других независимых переменных) для получения необходимых свойств объекта в заданный момент времени.
Комбинированное прогнозирование. Эвристическим и математическим методам прогнозирования присущи и преимущества, и недостатки. Комбинированный метод объединяет достоинства этих методов и сглаживает недостатки. Комбинированное прогнозирование имеет следующую последовательность действий. Из исследования модели процесса развития явления выявляются общие закономерности, при этом в них могут быть коэффициенты или функции, которые не удается определить на основании анализа моделей процесса. Эти коэффициенты (или функции) определяют статистическими методами. Полученные данные позволяют выполнить математический прогноз. Независимо от него осуществляется эвристический прогноз, и затем результаты эвристического и математического прогнозирования сравниваются. В случае их непротиворечивости, задачу прогнозирования можно считать решенной. В случае противоречивости прибегают к методу логического анализа, с помощью которого и принимают окончательное решение.
Метод наименьших квадратов (МНК) объективен. По своей сути он предназначен для обработки статистических данных, дискретных процессов. Однако, для него необходим достаточно большой статистический материал, необходимо знать вид функции, описывающий процесс, а также он не дает возможности предсказать «скачок» ни на участке упреждения, ни на участке наблюдения. МНК предполагает неизменность модели в области наблюдений и в области прогноза, «скачок» же – это изменение модели.
Методы оптимальной фильтрации (Винера – Хопфа, фильтр Калмана), предназначенные для обработки непрерывных статистических данных и рассчитанные, прежде всего, на применение в автоматических системах управления. Эти фильтры быстро и просто реализуются на ЭВМ, очень удобны для получения непрерывного прогноза, однако для них характерны: необходимость значительного статистического материала, знания корреляционной функции процесса и невозможность предсказания скачков на участке упреждения.
Кроме перечисленных методов, для прогнозирования применяют метод канонических разложений и метод прогнозирования с помощью моделирования процессов развития, который идеален в том случае, если процесс детально изучен. Для сложных процессов построить корректную модель часто не удается.
Рассмотренные способы прогнозирования характеристик процессов являются актуальными при допущении неизменности их моделей как на участке наблюдения за этими процессами, так и на участке прогнозирования. Однако не всегда параметры принятой модели не меняются. В большинстве случаев входные данные искажены помехой. Поэтому иногда трудно распознать, является ли отклонение нового наблюдения следствием внешнего воздействия, помехи или внутреннего воздействия. В последнем случае необходимо, чтобы модель позволяла как можно точнее описывать текущие данные о процессе, и совсем не обязательно, чтобы она также хорошо описывала данные, полученные в прошлом. Очень важно, чтобы прогнозирующая система могла автоматически распознавать изменения в модели. Одним из путей решения этой задачи является применение прогнозирования методом экспоненциального сглаживания. Сглаживание (аппроксимация) - подбор уравнения, которое полным образом описывает процесс математически.
Математическая модель экспоненциального сглаживания имеет вид:
.
(7)
– постоянная
(коэффициент) сглаживания;
-
прогнозное состояние объекта;
-
предыдущее значение прогноза;
-
текущее значение предыстории.
Текущее
значение сглаженной величины
равно сумме предыдущего ее значения и
некоторой доли разности между текущим
наблюдением и предыдущим значением
сглаженной величины. Величина
является линейной комбинацией всех
наблюдений, вес которых убывает по
геометрической прогрессии со временем.
Текущее наблюдение имеет вес A.Значение
задается экспериментальным методом
илежит в интервале (0, 1). Если коэффициент
А близок к 0, апроксимационная траектория
вытягивается из синусоиды в прямую.
При этом
,
т. е. значение S
настолько стабильное, что можно не
использовать новую информацию о процессе.
Напротив,
означает, что предшествующей информации
о процессе доверять нельзя. При применении
экспоненциального сглаживания для
определения коэффициента постоянной
модели A
необходимо знать предшествующее значение
оценки
и текущего наблюдения
.
Точность и скорость реакции системы на
изменение в модели зависят от величины
постоянной сглаживания A.
Малая величина A
обеспечивает большую точность оценки
A
при неизменной модели, но медленную
реакцию на изменение в модели, а увеличение
A
будет способствовать увеличению скорости
этой реакции.
В нашем случае элементами предыстории будут являться значения µ и α (для Н, Х, Y) на 14 моментов времени. Необходимо спрогнозировать состояние объекта на 15й момент времени, построить графики с прогнозными точками в фазовом пространстве и произвести оценку прогнозных значений.
(8)
(9)
Производим расчет прогнозных значений µ и α как реальных, так и предельных (µа, µв, αа, αв), при; А=0,3; А=0,7; А=0,9 для массива данных Н,Х,Y. Результаты вычислений приведены в таблицах на рисунках 10,11 .
По полученным данным строим графики прогнозирования экспоненциальным сглаживанием, которые изображены на рисунках 10,11.
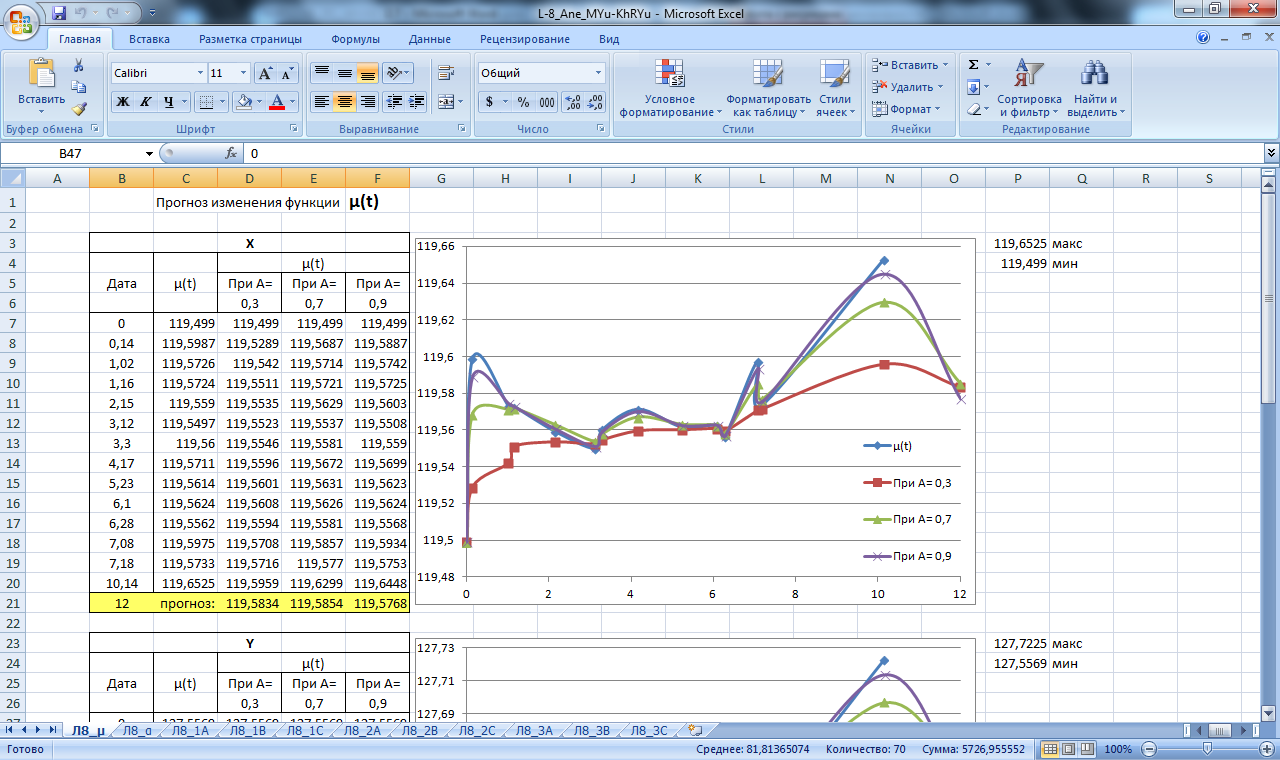
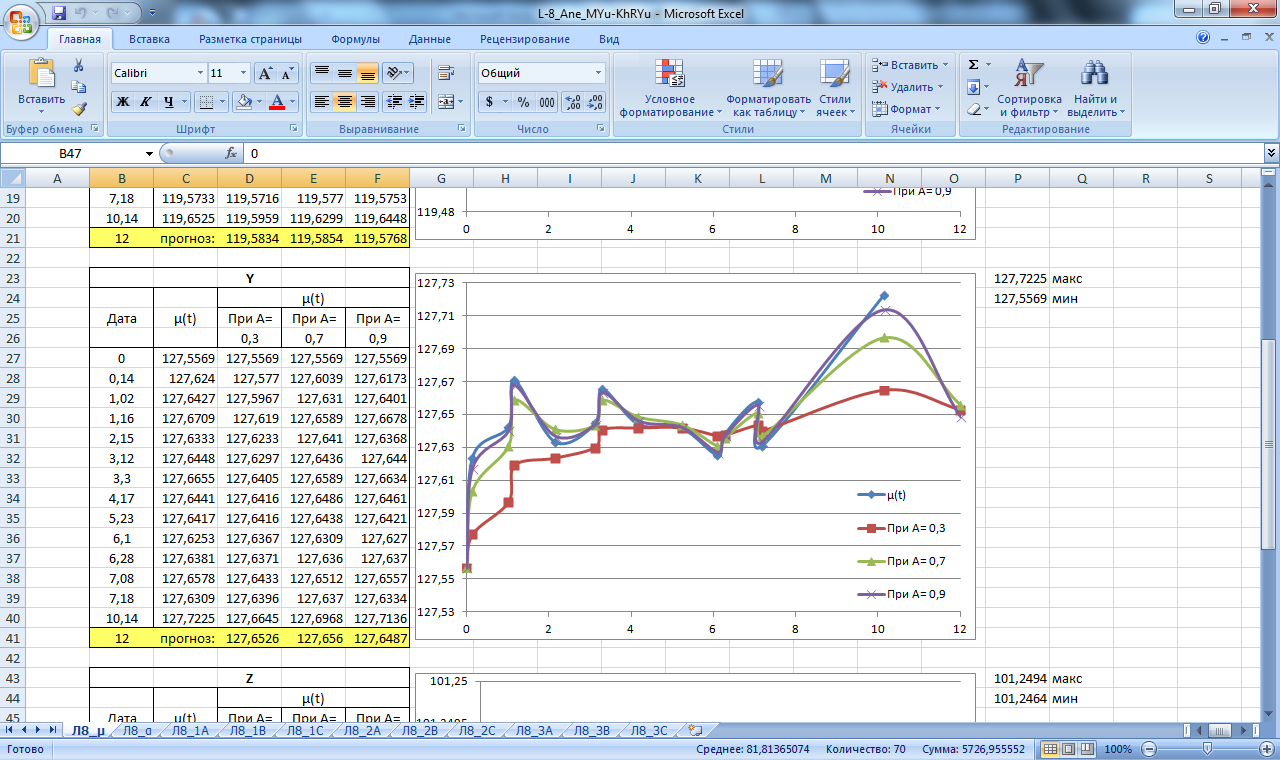
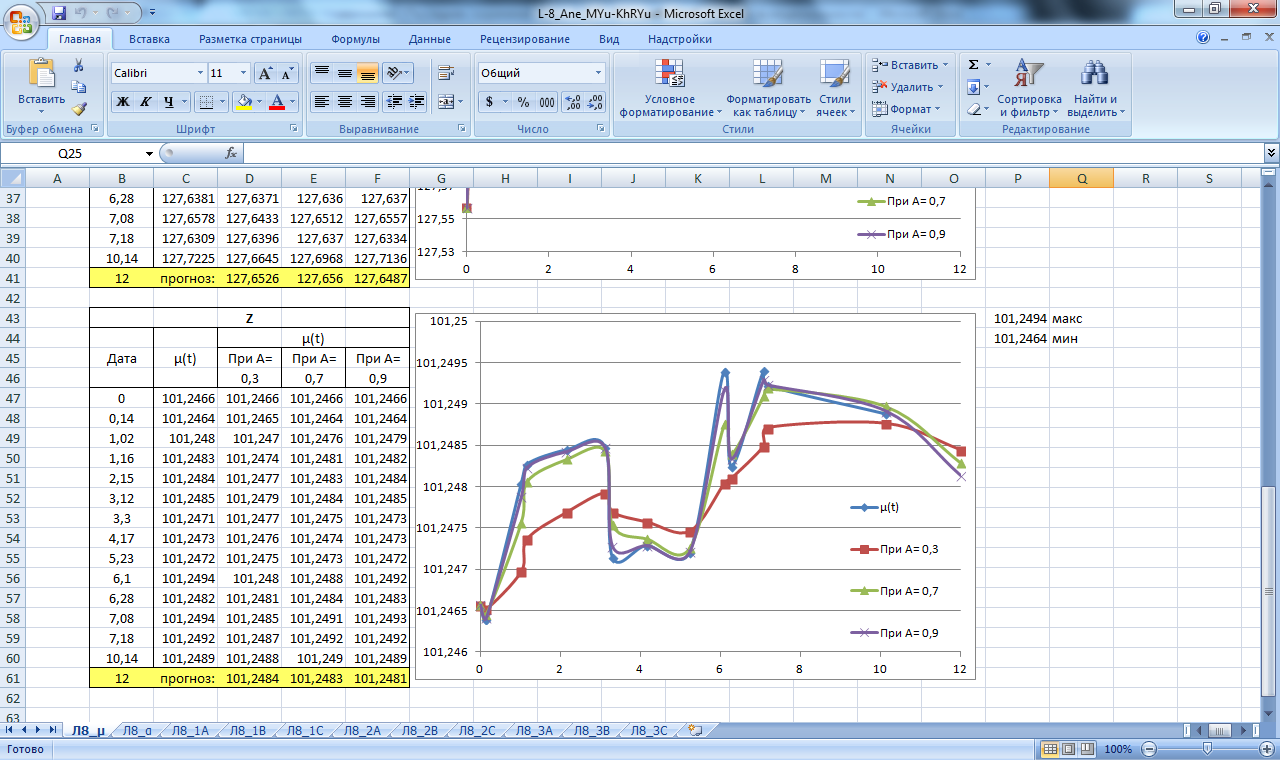
Рисунок 10. Значение сглаживающей функции µ. Прогнозирование экспоненциальным сглаживанием
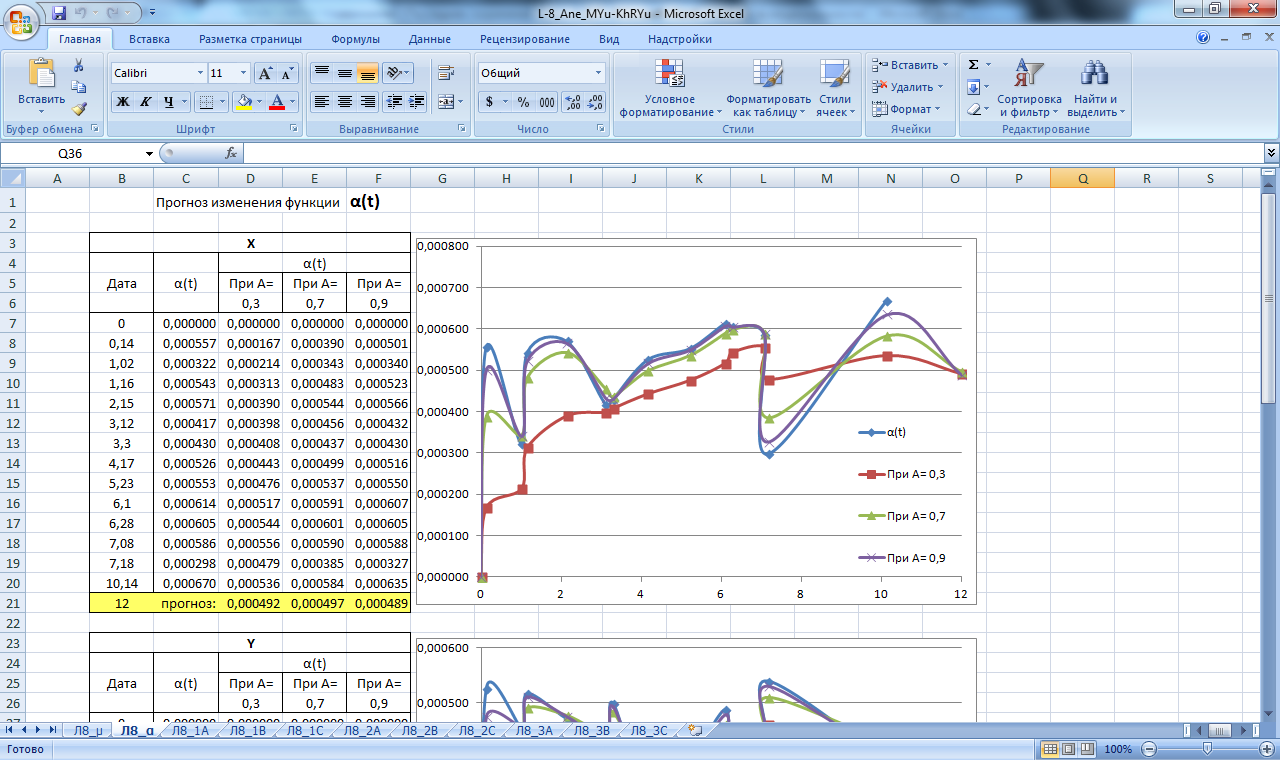
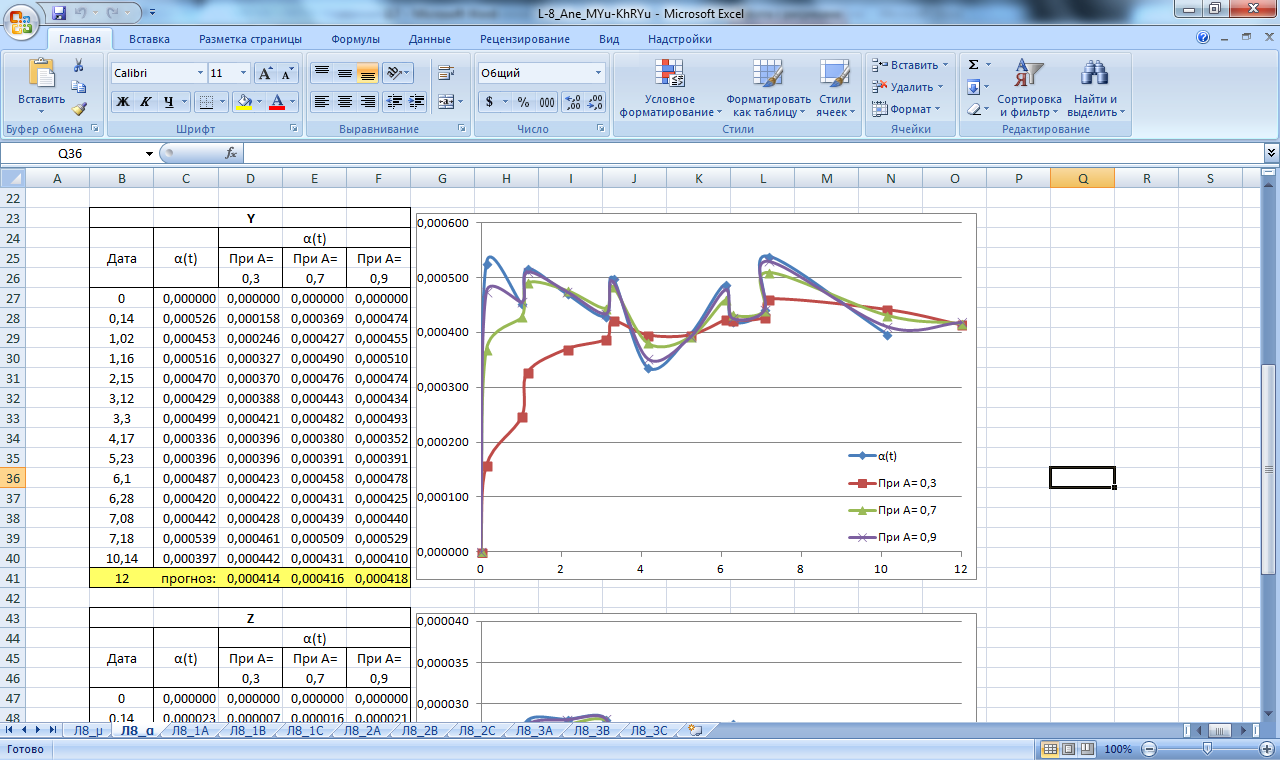
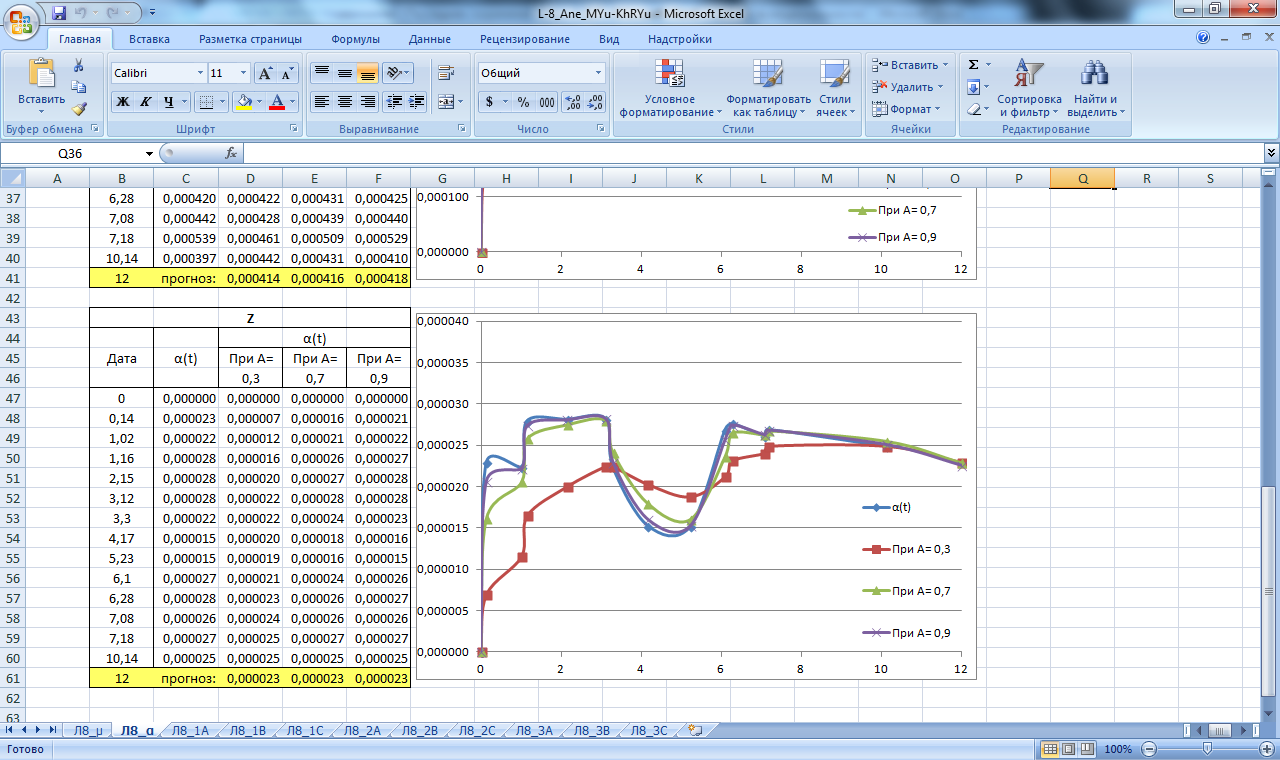
Рисунок 11. Значение сглаживающей функции α. Прогнозирование экспоненциальным сглаживанием.
Вывод: построены графики прогнозирования методом экспоненциального сглаживания. Полный анализ объекта возможно будет сделать после статистической оценки изменения пространственно-временного состояния объекта.