4.I уровень декомпозиции.

4.1 Разработка модели изменения состояния объекта в фазовом и гильбертовом пространствах.

Состояние объекта определим свойствами элементов системы геодезических точек. Любая система определена множеством элементов S_i (i=1,n) и множеством функций взаимосвязи между ними f_j (j=1,k).

Каждый элемент системы обладает, за счет функций взаимосвязи, общими свойства для всей системы, общими свойствами для соседних связанных с ним элементов, и индивидуальными свойствами. Элементы системы могут образовывать подсистемы элементов с функциональными связями характерными как для всей системы, так и для подсистемы индивидуально.

В связи с этим, состояние изучаемого объекта можно определить, как свойствами всей системы, геодезических точек, так и совокупностью свойств подсистем (в зависимости от конструктивных особенностей и от цели моделирования).

Состояние объекта определяется множеством его свойств (характеристик) в фиксированный момент времени. Состояние системы геодезических точек определяется множеством свойств элементов этой системы.

Условно, модель состояния системы можно изобразить, как показано на рисунке 5.

H₁

__

H₂ V

S_i,f _i

H_n

Рисунок 5.Модель состояния системы

Где H_i – множество свойств (координат геодезических пунктов), V – состояние объекта.

В качестве характеристик состояния системы примем высотные отметки геодезических точек. Тогда математическая модель состояния определится скалярной функцией (формула 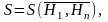1):

(1)

где n – количество высотных координат точек.

Каждое свойство, характеризующее объект, рассматривается как скалярная функция некоторого параметра (чаще всего – времени), а его численное значение – как координата на числовой оси, соответствующей этой скалярной функции. Таким образом, каждому свойству ставится в соответствие координатная ось. Тогда состояние объекта, соответствующее данному множеству свойств, представляется точкой в пространстве состояний, координаты которой равны численным значениям свойств. Размерность пространства состояний равна количеству свойств, принятых во внимание при описании состояний объекта. Такое пространство получило название фазового пространства, точки этого пространства называют фазовыми точками. В фазовом пространстве для описания состояния объекта допускается использование свойств различной физической природы

Любой точке фазового пространства сопоставляют вектор, координаты которого эквивалентны свойствам объекта. Тогда, модель состояния объекта - вектор с координатами равными значениям свойств объекта (формула 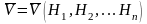2):

, (2)

где 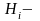численные значения свойств объекта (т.е. высотные отметки геодезических точек).

Множество состояний объекта образует фазовое пространство, где каждому его свойству сопоставляется координатная ось. Т.е. состояние объекта определится точкой в фазовом пространстве с координатами эквивалентными его свойствам. С течением времени объект приобретает новое состояние и следовательно фазовая точка займет другое положение в фазовом пространстве. След от перемещения точки в фазовом пространстве называется фазовой траекторией и характеризует тенденцию изменения состояния объекта с течением времени, т.е. эволюцию объекта.

Любой вектор определяется не только своими координатами, но модулем М и направлением . Модель эволюции, в этом случае, определяется двумя характеристиками М и , которые являются одновременно координатами в фазовом пространстве:

где

(3)

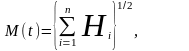(4)

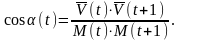(5)

Фазовое пространство определится параметрами t, M и .

На основании формулы (2) определим модель эволюции для исследуемого объекта

Модель эволюции системы V(t)=V(H1(t),H2(t),…,H12(t)).

Определив фазовые координаты функции M и  (таблицы 4,5,6), построим графики фазовых траекторий (рисунки 6,7,8).

М – фазовая координата определяющая неравномерность движения объекта в пространстве и времени (вращательное движение);

α – фазовая координата определяющая движения объекта в вертикальной плоскости (поступательное движение).

По формулам (4),(5) посчитаны координаты определяющие неравномерность движение объекта в пространстве и времени, а так же фазовые координаты определяющие движение объекта в вертикальной плоскости. Результаты приведены в таблицах №№4,5,6.

Таблица 4.Координата Н(м). µ, α- фазовые координаты.
Дата	1	2	3	4	5	6	7		8		9		10		11		12		µ(t)(у.е)		α(t)(у.е)
0	29,222	29,223	29,222	29,222	29,223	29,222	29,233		29,234		29,231		29,232		29,232		29,232		101,247		0,0000
0,16	29,222	29,222	29,223	29,222	29,223	29,222	29,233		29,232		29,232		29,232		29,232		29,232		101,246		0,00002
1,07	29,222	29,224	29,223	29,223	29,223	29,222	29,233		29,233		29,233		29,232		29,233		29,232		101,248		0,00002
1,14	29,223	29,223	29,223	29,223	29,222	29,222	29,233		29,233		29,233		29,234		29,232		29,232		101,248		0,00003
2,16	29,223	29,223	29,223	29,224	29,223	29,222	29,232		29,233		29,233		29,234		29,232		29,232		101,248		0,00003
3,20	29,223	29,224	29,224	29,223	29,223	29,222	29,232		29,233		29,233		29,234		29,232		29,232		101,248		0,00003
3,30	29,222	29,224	29,222	29,223	29,222	29,222	29,233		29,232		29,233		29,233		29,233		29,232		101,247		0,00002
4,19	29,222	29,224	29,222	29,223	29,222	29,222	29,233		29,233		29,232		29,232		29,232		29,232		101,247		0,00002
5,08	29,223	29,224	29,222	29,223	29,222	29,222	29,233		29,233		29,232		29,232		29,233		29,232		101,247		0,00002
6,19	29,223	29,224	29,223	29,223	29,223	29,223	29,233		29,233		29,233		29,233		29,233		29,233		101,249		0,00003
6,29	29,222	29,223	29,223	29,223	29,223	29,223	29,232		29,233		29,233		29,232		29,234		29,233		101,248		0,00003
8,08	29,223	29,224	29,223	29,223	29,223	29,223	29,233		29,234		29,234		29,232		29,234		29,233		101,249		0,00003
9,18	29,222	29,224	29,223	29,223	29,223	29,223	29,232		29,234		29,234		29,232		29,234		29,233		101,249		0,00003
10,14	29,222	29,224	29,223	29,223	29,223	29,223	29,233		29,233		29,233		29,233		29,233		29,233		101,249		0,00002

На основании таблицы № 4 построен график фазовой траектории для координат Н (рисунок 6).

Рисунок 6. График фазовой траектории

для координат Н

Дата	1	2	3	4	5	6	7	8	9	10	11	12	µ(t)(у.е)	α(t)(у.е)
0,00	20,00	5,00	5,00	20,00	26,50	40,00	21,00	36,50	45,00	51,50	51,50	45,00	119,499	0,000000
0,16	20,02	5,03	5,04	20,04	26,51	40,04	21,05	36,54	45,03	51,54	51,54	45,01	119,599	0,000557
1,07	20,01	5,01	5,00	20,04	26,50	40,02	21,03	36,52	45,04	51,54	51,52	45,02	119,573	0,000322
1,14	20,02	5,05	5,02	20,02	26,50	40,03	21,03	36,54	45,01	51,54	51,51	45,03	119,572	0,000543
2,16	20,05	5,01	5,01	20,05	26,52	40,01	21,03	36,50	45,04	51,53	51,51	45,01	119,559	0,000571
3,20	20,02	5,03	5,01	20,03	26,53	40,01	21,02	36,53	45,01	51,51	51,52	45,01	119,550	0,000417
3,30	20,04	5,01	5,01	20,02	26,50	40,02	21,02	36,53	45,00	51,50	51,55	45,02	119,560	0,000430
4,19	20,03	5,05	5,02	20,00	26,53	40,01	21,03	36,52	45,04	51,52	51,52	45,04	119,571	0,000526
5,08	20,00	5,01	5,03	20,04	26,51	40,04	21,05	36,53	45,02	51,50	51,53	45,01	119,561	0,000553
6,19	20,04	5,01	5,05	20,02	26,54	40,02	21,02	36,51	45,04	51,50	51,52	45,03	119,562	0,000614
6,29	20,02	5,03	5,03	20,04	26,55	40,04	21,01	36,53	45,00	51,50	51,50	45,02	119,556	0,000605
8,08	20,04	5,00	5,05	20,03	26,54	40,05	21,04	36,52	45,05	51,52	51,52	45,03	119,597	0,000586
9,18	20,01	5,00	5,01	20,04	26,52	40,01	21,01	36,52	45,04	51,52	51,55	45,03	119,573	0,000298
10,14	20,05	5,05	5,05	20,05	26,55	40,05	21,05	36,55	45,05	51,55	51,55	45,05	119,653	0,000670

Таблица 5. Координаты Х. µ, α- фазовые координаты.

На основании таблицы № 5 построен график фазовой траектории для координат Х (рисунок 7).

Рисунок 7. График фазовой траектории для координат Х

Таблица 6. Координаты У. µ, α- фазовые координаты.
Дата	1	2	3	4	5	6	7		8		9		10		11		12		µ(t)(у.е)		α(t)(у.е)
0,00	21,00	21,00	29,50	29,50	35,50	35,50	21,00		36,50		45,00		51,50		51,50		45,00		127,5569		0,000000
0,16	21,04	21,05	29,52	29,53	35,55	35,51	21,02		36,50		45,02		51,50		51,52		45,02		127,6240		0,000526
1,07	21,05	21,01	29,51	29,54	35,55	35,51	21,03		36,51		45,03		51,52		51,54		45,02		127,6427		0,000453
1,14	21,04	21,04	29,51	29,54	35,55	35,55	21,01		36,54		45,02		51,51		51,55		45,05		127,6709		0,000516
2,16	21,04	21,00	29,55	29,54	35,51	35,54	21,03		36,51		45,01		51,53		51,53		45,02		127,6333		0,000470
3,20	21,04	21,02	29,52	29,53	35,51	35,53	21,05		36,54		45,03		51,52		51,52		45,02		127,6448		0,000429
3,30	21,04	21,05	29,54	29,54	35,52	35,54	21,03		36,55		45,02		51,54		51,54		45,01		127,6655		0,000499
4,19	21,04	21,00	29,55	29,52	35,52	35,52	21,01		36,52		45,03		51,53		51,53		45,03		127,6441		0,000336
5,08	21,05	21,01	29,53	29,53	35,50	35,53	21,03		36,53		45,02		51,53		51,52		45,03		127,6417		0,000396
6,19	21,04	21,03	29,51	29,53	35,51	35,51	21,02		36,52		45,04		51,50		51,51		45,05		127,6253		0,000487
6,29	21,04	21,02	29,54	29,50	35,51	35,54	21,02		36,53		45,04		51,52		51,52		45,01		127,6381		0,000420
8,08	21,04	21,03	29,52	29,50	35,53	35,55	21,04		36,54		45,01		51,53		51,54		45,04		127,6578		0,000442
9,18	21,05	21,05	29,51	29,53	35,51	35,51	21,04		36,52		45,03		51,51		51,54		45,00		127,6309		0,000539
10,14	21,05	21,05	29,55	29,55	35,55	35,55	21,05		36,55		45,05		51,55		51,55		45,05		127,7225		0,000397

На основании таблицы № 6 построен график фазовой траектории для координат У (рисунок 8).

Рисунок 8. График фазовой траектории для координат У

По заданной математической модели изменения состояния объекта в гильбертовом пространстве построен график функции 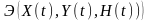, где 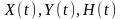, вычисляются по формуле (6)

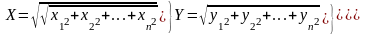
X_г (м)

Y_г (м)

H_г (м)

(6)

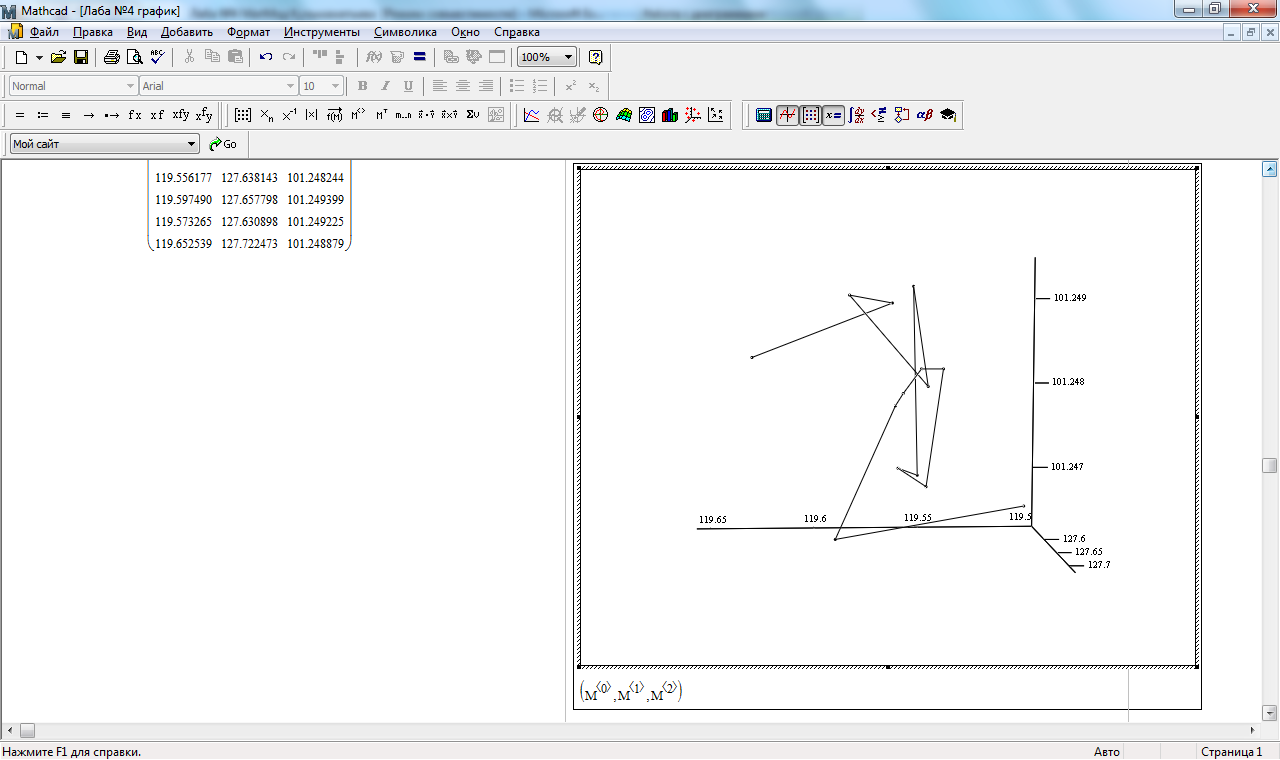
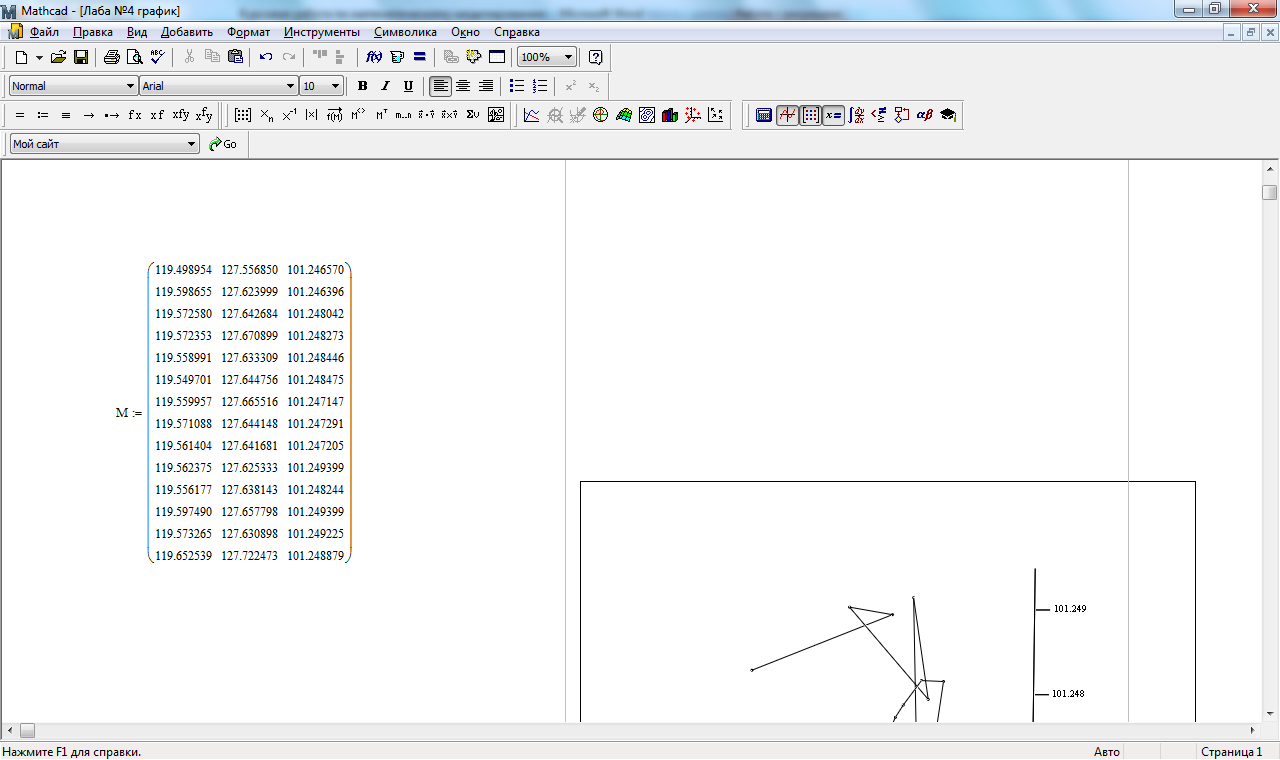
H_г (м)

X_г(м)

Y_г (м)

Рисунок 9. График траектории и значения координат в гильбертовом пространстве.

Анализируя полученные графики траекторий координат, можно заметить, что на всех рисунках наблюдается тенденция изменения на протяжении периода исследования. Это может характеризоваться воздействием внешних факторов или ошибкой измерений.