3. Построение концептуальной модели изменения пространственно-временного состояния объекта в трехмерном пространстве. Алгоритмизация. Формализация.

Следующий этап построения модели системы – разработка алгоритма.

Алгоритм – это точное предписание последовательности действий для достижения указанной цели.

Главными свойствами алгоритма являются результативность, массовость (универсальность, понятливость и конечность (дискретность))

Множество геодезических контрольных точек представляет с объектом одно целое – это есть система, которая может изменять свои значения в пространстве и времени. Любую систему можно изучить, применяя приёмы и методы системного анализа.

Существует два метода системного анализа:

1. классический, основанный на принципе агрегирования (от частного к общему);

2. системный, основанный на принципе декомпозиции (от общего к частному).

Модель изменения состояния объекта методом системного подхода должна отображать процесс изменения пространственно-временного состояния всей системы одной функции координат и времени.

Создание системы контроля состояний объекта делает необходимым формулирование следующих задач:

1. оперативное предоставление объективной информации о состоянии объекта в целом;

2. определение выхода состояния объекта за критический уровень;

3. определение границ структурных частей объекта;

4. прогнозирование будущего состояния объекта.

Р ешение этих задач невозможно без применения методов системного анализа, который дает объективную информацию об изменении всего объекта и его частей. Процедура декомпозиции системы имеет иерархическую структуру, состоящую из k уровней детализации. При этом величина k зависит как от степени сложности самого объекта, так и от вида, скорости движения, влияющего на изменение его состояния, и имеет предельное значени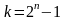е , где 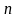– количество точек системы. Критерием принятия решения о переходе от уровня к уровню является проверка условий выхода состояния объекта за предельно допустимые границы. При определенных обстоятельствах декомпозиция может осуществляться до уровня неделимого элемента системы – геодезического знака. В этом случае анализ системы контроля переходит к классическому виду.

Следуя структурной схеме (рисунок 3) рассмотрим процедуру декомпозиции на примере модели объекта (рисунок 2).

Блок в

Блок с Блок а

Рисунок 2. Модель объекта.

П оток сигналов X, поступающих на вход системы

I уровень декомпозиции.

1.Разработка модели  изменения состояния объекта в фазовом и гильбертовом пространствах

2.Прогнозирование функции объекта

3.Оценка математической модели пространственно-временного состояния объекта

II уровень декомпозиции

1.Определение пространственно-геометрических характеристик объекта. Построение математической модели пространственно-временного состояния объекта

2. Прогнозирование функции объекта

3.Статистический метод оценки изменения пространственно-временного состояния объекта

Выходные сигналы Y

Рисунок 3. Структурная схема декомпозиции

I уровень декомпозиции представляет собой исследование поведения системы в различные моменты времени. Изменение состояния объекта обусловлено изменением свойств объекта относительно времени.

II уровень декомпозиции представляет собой моделирование блоков в системе в пространстве и времени относительно друг друга. Структурная схема подразделяется на подсистемы, определённые частями объекта. На данном этапе необходимо сравнять количество марок на блоках, привести их к общему знаменателю (если марки уже расставлены) или же распределить имеющееся количество марок относительно блоков системы в равном количестве. Дальнейшее исследование ведётся по тому же алгоритму, что и на I уровне декомпозиции.

На рисунке 4 представлена типовая схема моделирующего алгоритма, построенная по блочному принципу. Схема состоит из четырех модулей.

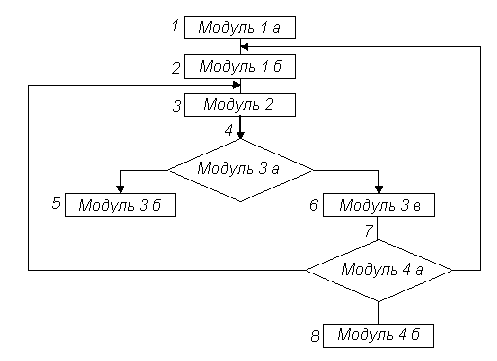
Рисунок 4. Типовая схема моделирующего алгоритма

Согласно математическому описанию модели изменения состояний объектов по геодезическим данным, содержание программных модулей следующее:

• модуль 1 – формирование начальных значений состояний объекта:

а) начальные значения состояния объекта

,

где 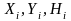– координаты геодезических марок 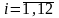приходящихся на нулевую эпоху;

б) начальные значения состояния объекта для одного прогона модели (указываются отметки марок из множеств 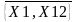, , 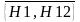учитываемых при анализе состояния объекта для одного прогона (рисунок 3));

• модуль 2 – определение очередного момента изменения состояния объекта, где 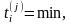и выбор блока ;

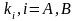• модуль 3 – логическое переключение:

а) переход по номеру блока 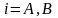и по времени Т (принятие решения о завершении прогона);

б) фиксирование информации о переходе системы (блока) из состояния в состояние (в графической интерпретации выражается очередной точкой функции, определяющей состояние объекта в фиксированный момент времени с фазовыми координатами M и 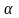, эквивалентными значениям множества отметок геодезических знаков);

в) завершение прогона, если ;

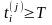• модуль 4 – управление и обработки информации:

а) проверка точности результатов моделирования (расчет предельно допустимых границ, в рамках которых состояние объекта можно считать устойчивым);

б) окончательная обработка информации и подготовка результатов моделирования к передаче на выход модели системы.

Данная схема моделирующего алгоритма является укрупненной и в разных случаях может быть уточнена и дополнена модулями для варьирования структурой объекта.

Каждый элемент системы обладает, за счёт функций взаимосвязи, общими свойствами для всей системы, общими свойствами для соседних связанных с ними элементов, и индивидуальными свойствами. Элементы системы могут образовывать подсистемы элементов с функциональными связями характерными как для всей системы, так и для подсистемы индивидуально.

В связи с этим, состояние изучаемого объекта можно определить, как свойствами всей системы, геодезических точек, так и совокупностью свойств подсистемы (в зависимости от конструктивных особенностей и от цели моделирования).

Состояние объекта определяется множеством его свойств (характеристик) в фиксированный момент времени. Состояние системы геодезических точек определяется множеством свойств элементов этой системы.

Целью моделирования является описание движения системы в целом. В данной курсовой работе объект моделирования сложный и обладает большим количеством свойств, то необходим тот метод, который бы учитывал все эти свойства. Исходя из перечисленного, для курсовой работы приемлем метод фазового пространства, в котором каждому свойству объекта сопоставлена своя координатная ось. Каждая точка этого пространства (фазовая точка) характеризует одно из состояний объекта. Кривая, отображающая изменение состояния объекта – фазовая траектория.

Методы реализации математических моделей определяются формой представления мо­дели, целями моделирования, имеющимися техническими ресурсами и т.д. Выделяют два метода реализации математических моделей: аналитический и численный.

Аналитический метод применяют к моделям, представленным в аналитической или инва­риантной форме. В этом случае установлена аналитическая зависимость искомых резуль­татов от исходной информации, множества состояний объекта и других его характери­стик. Эта зависимость чаще всего выражена явной или неявной функцией и может быть исследована методами математического анализа. В результате такого исследования фор­мулируются выводы о существовании решения его единственности, диапазоне допусти­мых значений, зависимости решения от изменений исходной информации и другие, глав­ный образом, качественные характеристики самой модели и результатов моделирования, количественные характеристики находят при численной реализации математической мо­дели.

Численные методы реализации модели основаны на выполнении вычислительного экспе­римента, т.е. совместном использовании математического анализа, вычислительной мате­матики и технических средств для получения ответов на разумно поставленные вопросы математического и физического содержания. В настоящее время технология вычислительного эксперимента делится на ряд этапов.

На первом этапе, на основе имеющейся модели разрабатывается вычислительный алгоритм, т. е. определяется совокупность алгебраических формул, по которым будут выполняться вычисления, и логических условий, устанавливающих необходимую последовательность применения этих фор­мул. Для одной и той же модели можно предложить множество вычислительных алгоритмов, сре­ди которых необходимо выбрать экономически целесообразный алгоритм, обеспечивающий полу­чение результатов моделирования с заданной точностью.

На втором этапе разрабатывается программа для выполнения вычислений на ЭВМ.

На третьем этапе выполняются расчеты на ЭВМ. Этот этап имеет наибольшее сходство с фи­зическим (натурным) экспериментом. На этом этапе обязательно производятся, так называемые, тестовые расчеты, необходимые для выявления и устранения оши­бок, допущенных при создании математической модели, организации вычислительного экспери­мента и составлении программы для ЭВМ.

Четвертый этап вычислительного эксперимента состоит в обработке и анализе результатов вычислений. Итог этого этапа - принятие решения о приемлемости результатов или необходимости внесения изменений в модель, алгоритм или программу.

Постоянно возрастающая сложность и объем вычислений не компенсируются возрас­тающей мощностью ЭВМ. Поэтому необходимо постоянное совершенствование матема­тических моделей, вычислительных алгоритмов и программ. Эти обстоятельства привели к созданию качественно новой методологии исследования объектов методом математиче­ского моделирования, которая получила название имитационное моделирование.

В качестве средств реализации математического аппарата выбираем программный продукт МаthСad, так как данный продукт прост в использовании и подходит для выполнения как простых, так и сложных вычислений и операций, имеет ряд встроенных функций и позволяет пользователю программировать свои, а также позволяет визуализировать полученные результаты (в виде 2-мерных, 3-мерных графиков, диаграмм и т. д.), в общем обладает всеми функциями, необходимыми для реализации выбранного математического аппарата.