32. Знакозмінні ряди. Ознака Лейбніца. Абсолютна та умовна збіжність.

Ряд називається знакозмінним, якщо він містить нескінченну кількість, як додатніх, так і від’ємних членів. Ряд члени якого по черзі мають додатній та від’ємний знаки, називається знакопочережним.

Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду.

Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається.

Для виявлення умовної збіжності знакопочережного ряду використовують наступну ознаку:

Ознака Лейбніца. Якщо абсолютні величини знакопочережного ряду монотонно спадають і границя абсолютної величини загального члену ряду дорівнює нулю при , то ряд збігається, причому його сума S не перевищує першого члена ряду.

32. Функціональні ряди. Степеневий ряд. Область збіжності. Ряд Тейлора і Маклорена.

Ряд називається функціональним, якщо його члени є функціями.

,

Якщо замість х підставити деяке число х₀, то матимемо числовий ряд, який може бути збіжний або розбіжний.

Якщо числовий ряд збігається, то точку х₀ називають точкою збіжності функціонального ряду.

Сукупність усіх точок збіжності функціонального ряду називається областю його збіжності.

Степеневим рядом називається ряд виду

Радіус збіжності R знаходиться за формулою ,

a_n – коефіцієнт при степеневій функції. Інтервал - називається інтервалом збіжності.

Питання збіжності ряду при розв’язується для кожного ряду окремо.

• якщо , то ряд збіжний лише в точці ;

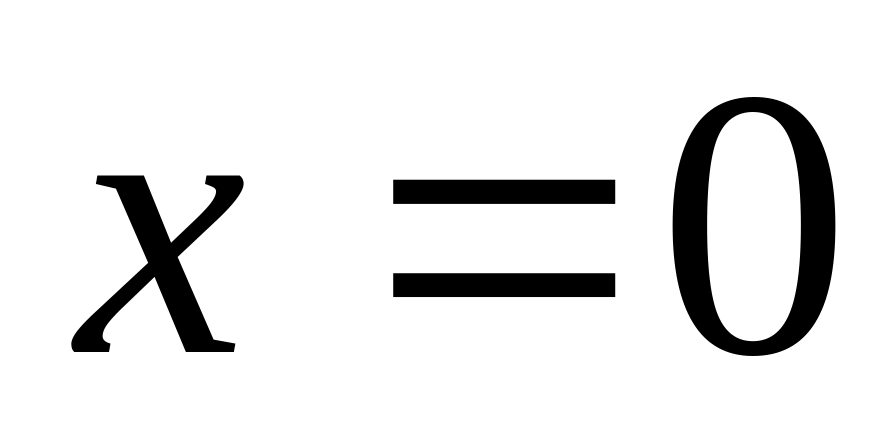• якщо , то ряд збіжний на всій числовій осі.

Радіус збіжності ряду визначається за тими ж формулами, але інтервал збіжності знаходять з нерівності , , ,

Ряд Тейлора:

Якщо , то ряд називається рядом Маклорена:

Використовують в наближених обчисленнях наступні розклади, в яких змінна х замінена змінною U:

1) ,

2) ,

3) ,

4) ,

5) ,

6) ,

7) ,