26. Опуклість та вгнутість. Точки перегину. Дослідження за допомогою похідної.

Плоска крива L називається опуклою в точці , якщо точки кривої, що суміжні з точкою і лежать по обидва боки від неї, розміщені нижче дотичної до кривої, проведеної через цю точку.

Якщо друга похідна функції у даному проміжку є від’ємною, то графік її є опуклим у цьому проміжку.

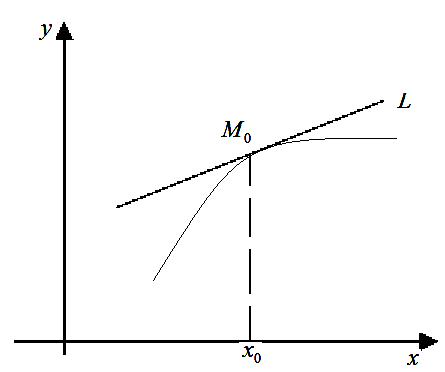
Плоска крива L називається вгнутою в точці , якщо точки кривої, що суміжні з точкою і лежать по обидва боки від неї, розміщені вище дотичної до кривої, проведеної через цю точку.

Якщо друга похідна функції у даному проміжку є додатною, то графік її є вгнутим у цьому проміжку.

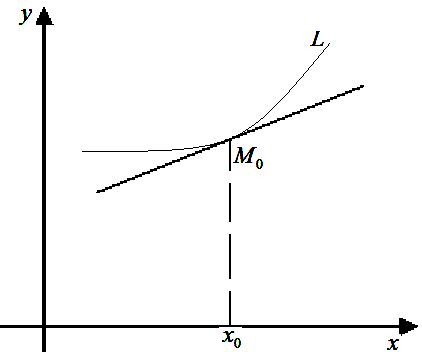
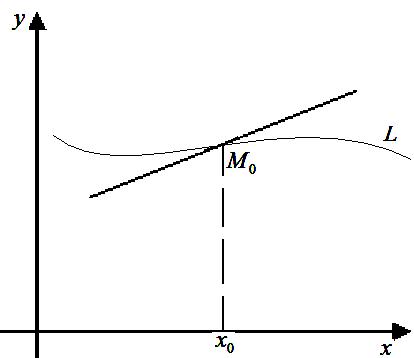
Точкою перегину кривої L називається точка , яка відділяє опуклу частину кривої від вгнутої.

Достатня ознака точки перегину: якщо при додатному друга похідна функції дорівнює нулю і при переході аргументу через дане значення вона змінює знак, то точка є точкою перегину.

27. Поняття функції багатьох змінних. Способи задання. Область визначення.

Відповідність при які кожній парі , відповідає єдине значення , називається функцією двох змінних. - символічний запис функції з двома змінними.

Множина всіх пар для яких функція має зміст називається областю визначення, позначається .

Аналогічно означається функція n-змінних.

Способи задання функцій:

• графічний (множиною точок координатної площини);

• табличний (функція задається таблицею);

• аналітичний (задається формулою);

• область визначення.

27. Частинні похідні та частинні диференціали функцій. Повний диференціал та його застосування.

Нехай задано функція від двох змінних фіксуючи одну із змінних (наприклад ) ми маємо функцію від однієї змінної .

Частинною похідною по змінній називається границя відношення приросту функції по до при умові, що . Позначається , , , , .

Щоб знайти частинну похідну по , вважають сталим, а  змінною.

Частинною похідною по змінній називається границя відношення приросту функції по до при умові, що . Позначається , , , , .

Щоб знайти частинну похідну по , вважають сталим, а  змінною.

Якщо частинні похідні і функції неперервні в даній області, то її повне перетворення представляється в кожній точці цієї області у вигляді

,

де при і

( )

Приріст частинної функції називається повним диференціалом функції і позначається через або .

Якщо , то ,

або

27. Первісна функція. Невизначений інтеграл. Таблиця невизначених інтегралів. Методи інтегрування.

Функція називається первісною для функції на заданому проміжку, якщо для всіх з цього проміжку справедлива рівність .

Якщо є первісною для функції , то для будь-якої сталої функція є первісною для функції .

 невизначений інтеграл від функції ;

 первісна для функції ;

 підінтегральний вираз.

Похідна від первісної для функції на заданому проміжку дорівнює підінтегральній функції

Операція знаходження множини всіх первісних функцій для даної функції називається невизначеним інтегруванням і є оберненою операцією до диференціювання. На відміну від диференціювання невизначений інтеграл від елементарної функції не завжди є елементарною функцією.

Властивості невизначеного інтеграла:

1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції

2. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу

3. Знак інтеграла перед знаком диференціала знищує останній, але при цьому вводиться довільний сталий доданок

4. Сталий множник можна виносити за знак інтеграла

5. Інтеграл від алгебраїчної суми функцій дорівнює алгебраїчній сумі інтегралів від даних функцій

Наслідок: інтеграл від лінійної комбінації функції дорівнює лінійній комбінації інтегралів від заданих функцій з тими самими коефіцієнтами.

Таблиця невизначених інтегралів:

1. ; 14.

2. 15.

3. 16.

4. 17.

5. ; 18.

6. 19.

7. 20.

8. 21.

9. 22.

10. 23.

11. 24.

12. 25.

13.

Методи інтегрування:

1. Метод безпосереднього інтегрування полягає в тому, що підінтегральну функцію перетворюють до вигляду табличних функцій.

2. Метод підстановки (заміни змінної)

3. Метод інтегрування частинами

27. Визначений інтеграл та його застосування для розв’язання задач.

Криволінійна трапеція – це геометрична фігура обмежена кривою , прямими , та віссю .

; ;  диференціал змінної площі

Визначеним інтегралом від функції на відрізку називається границя інтегральної суми за умови, що , а , якщо ця границя існує і не залежить від способу розбиття відрізка на менші відрізки і від вибору ;

Геометричний зміст інтеграла: якщо , то чисельно дорівнює площі криволінійної трапеції.

Властивості визначеного інтеграла:

1)

2)

3)

4)

5)

Формула Ньютона-Лейбніца: .

27. Основні означення і поняття диференціального рівняння. Диференціальні рівняння з відокремлюваними змінними.

Диференціальним рівнянням називається рівняння, яке зв’язує незалежну змінну х, функцію у та її похідну .

Диференціальне рівняння може не містити явно х або у, але обов’язково має містити похідну .

Порядком диференціального рівняння називається порядок вищої похідної, що входить в дане рівняння.

Розв’язати диференціальне рівняння це означає знайти функцію при підстановці якої в дане рівняння одержимо тотожність.

Загальним розв’язком диференціального рівняння називається такий розв’язок, в який входить стільки незалежних сталих, який порядок рівняння.

Якщо в загальний розв’язок підставити початкові умови х₀, у₀ знайти С, С підставити в загальний розв’язок матимемо частинний розв’язок.

Диференціальним рівнянням з відокремлюваними змінними називається рівняння виду , де - функція від х, - функція від у.

Алгоритм розв’язання диференціальним рівнянням з відокремлюваними змінними:

1. Заміняємо ,

2. Відокремлюємо змінні

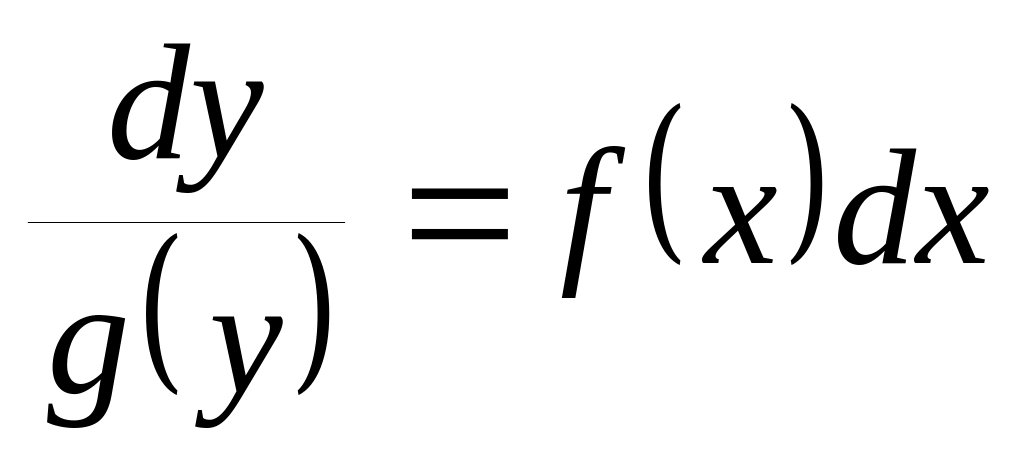
3. Інтегруємо . Знаходимо загальний розв’язок.

4. Якщо задані початкові умови х₀, у₀, то при підстановці їх в загальний розв’язок знаходимо С, С підставивши в загальний розв’язок матимемо частинний розв’язок.

32. Лінійні та однорідні диференціальні рівняння першого порядку. Алгоритм їх розв’язання.

Лінійні диференціальні рівняння першого порядку – це рівняння виду

, де - функції від х.

Алгоритм розв’язання лінійного диференціального рівняння першого порядку:

1. Заміняємо (UV – функції від х), то : .

2. З другого і третього доданків виносимо U за дужки: .

3. Функцію V знаходимо з рівності - диференціальне рівняння з відокремлюваними змінними V, x. .

4. Знайдену функцію V підставляємо в рівність (1) і знаходимо функцію U.

5. Записати , якщо задані початкові умови, то знайти частинний розв’язок.

Функція називається однорідною n-го порядку ,якщо замінивши матимемо дану функцію , ,

Однорідним диференціальним рівнянням першого порядку називається рівняння виду

, де - однорідні функції.

Алгоритм розв’язання однорідного диференціального рівняння першого порядку:

Заміняємо , де z – функція від х, . Такою підстановкою рівняння зводиться до диференціального рівняння з відокремлюваними змінними z та x.

32. Диференціальні рівняння вищих порядків. Лінійні диференціальні рівняння другого порядку із сталими коефіцієнтами. Алгоритм їх розв’язання.

Диференціальне рівняння другого порядку – це рівняння виду

Загальний розв’язок диференціального рівняння другого порядку – це функція, яка залежить від х та констант С₁,С₂.

Приклад: , , .

Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами – це рівняння виду , де p, g – сталі числа.

Алгоритм розв’язання лінійного однорідного диференціального рівняння другого порядку зі сталими коефіцієнтами:

Складаємо характеристичне рівняння:

Загальний розв’язок має вигляд:

1 вип. Якщо k₁, k₂ – дійсні різні числа : (D>0) .

2 вип. Якщо k=k₁=k₂ : (D=0) .

3 вип. Якщо корені комплексні числа : , , (D<0) .

32. Числові ряди. Збіжність ряду. Необхідна ознака збіжність ряду. Гармонічний ряд і ряд геометричної прогресії.

Рядом називається вираз виду

- члени ряду; - загальний член ряду.

Розглянемо деякі ряди :

1. Гармонічний ряд – це ряд, що складається з обернених до натуральних чисел.

Якщо в узагальненому гармонічному ряді : , то ряд збіжний, , то ряд розбіжний.

2. Ряд геометричної прогресії:

Сума перших n-членів ряду називається частинною сумою (S_n)

; ;

Збіжність ряду геометричної прогресії:

Якщо послідовність частинних сум збіжна, тобто існує границя , то такий ряд називається збіжним. ( S – сума ряду ) Ряд геометричної прогресії збіжний, коли .

Якщо границя - не існує або дорівнює , то ряд називається розбіжним.

Необхідна ознака збіжності ряду. Якщо ряд збіжний, то його загальний член прямує до нуля.

32. Знакододатні ряди, достатні ознаки збіжності.

Ознаки збіжності числових рядів з додатніми членами.

Перша порівняльна ознака. Нехай треба дослідити збіжність ряду . Візьмемо відомий збіжний числовий ряд . Якщо члени (1) не перевищують відповідних членів ряду (2) , , …, …, тоді ряд (1) збігається і його сума не перевищує суми ряду (2).

Друга порівняльна ознака. Нехай треба дослідити збіжність ряду . Візьмемо відомий розбіжний числовий ряд . Якщо члени (1) не менше відповідних членів ряду (2) , , …, …, то і ряд (1) розбіжний.

Ознака Даламбера. Якщо для додатнього числового ряду існує границя , то при D<1 - ряд збіжний, D>1 - ряд розбіжний.

Зауваження. Якщо D=1, то за цією ознакою неможливо визначити збіжність або розбіжність ряду.

Радикальна ознака Коші. Якщо для додатнього числового ряду існує границя , то при K<1 - ряд збіжний, K>1 - ряд розбіжний.

Зауваження. Ця ознака використовується найчастіше у випадках, коли загальний член ряду містить n в основі та показнику степеня.

Інтегральна ознака Коші. . Нехай треба дослідити збіжність ряду , . Розглянемо невласний інтеграл , в якому підінтегральна функція одержана шляхом заміни аргументу n на х в функції .

Зауваження. Інтегральна ознака Коші є найбільш сильною ознакою її використовують, коли не можна використати ознаки Даламбера (D=1) та радикальну ознаку Коші (K=1). Якщо невласний інтеграл збігається, то числовий ряд також збігається. Якщо невласний інтеграл розбігається (=). То ряд також розбіжний.