
- •Алгебраїчна форма комплексного числа. Дії над комплексними числами заданими в алгебраїчній формі.
- •Геометричні задання комплексних чисел. Модуль і аргумент. Тригонометрична і показникові форми комплексного числа.
- •Поняття відсотка, три типи задач на відсотки. Формули простого і складного відсотків.
- •Визначники та їх властивості. Формули Крамера.
- •Векторний і мішаний добуток векторів.
- •Поділ відрізка у даному відношенні. Відстань між двома точками. Полярна система координат.
- •Основні означення і поняття, рівняння еліпса, гіперболи, параболи.
- •Похідні основних елементарних функцій
- •Опуклість та вгнутість. Точки перегину. Дослідження за допомогою похідної.
- •Первісна функція. Невизначений інтеграл. Таблиця невизначених інтегралів. Методи інтегрування.
- •Знакозмінні ряди. Ознака Лейбніца. Абсолютна та умовна збіжність.
- •Функціональні ряди. Степеневий ряд. Область збіжності. Ряд Тейлора і Маклорена.
Похідні основних елементарних функцій
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила диференціювання
Властивості похідної
Похідна суми (різниці) функцій U(x) і V(x):

Похідна добутку :

Похідна частки:
 ;
;

Сталу с можна виносити за знак похідної:
 ; с=const
; с=const
Похідна складеної функції
Нехай
y=f((x))-cкладена
функція, тобто y=f(U),
U=(x).Тоді
![]()
Тобто, похідна складеної функції по незалежній змінній х дорівнює добутку похідної від даної функції по проміжній змінній U на прохідну проміжної змінної по незалежній змінній.
Геометричний та механічний зміст похідної. Дотична і нормаль до графіка функції.
Геометричний
зміст похідної.
Значення
похідної функції y=f(x)
в
точці х=х0,
тобто
![]()
Механічний зміст похідної. Похідна функції y=f(x) в точці х виражає швидкість зміни функції в точці х, тобто швидкість проходження процесу, що описується залежністю y=f(x).
Дотична і нормаль до графіка функції.
На малюнку показані дотична і нормаль до графіка функції y=f(x) в точці з координатою х=х0.
![]() дотична,
дотична,
![]()
нормаль,
нормаль,
![]()
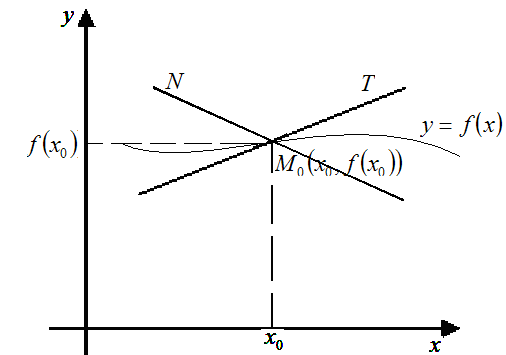
Рівняння дотичної до графіка функції у точці для
![]()
Рівняння нормалі до графіка функції у точці для
![]() ;
(
;
(![]() )
)
Диференціал функції. Застосування диференціала до наближених обчислень. Диференціали вищих порядків.
Диференціал функції – головна частина приросту функції.
![]()
Диференціали вищих порядків
Похідна 2-го порядку – це похідна від похідної 1-го порядку. Аналогічно диференціали.
Похідна наявної та параметричної функції. Правило Бернулі-Лопіталя.
Похідна
функції, заданої наявно.Якщо
функція y=f(x)
задана рівнянням F(x,y)=0,
не разв'язаним відносно у, то вона
називається заданою неявно і її похідна
![]() знаходиться
за формулою:
знаходиться
за формулою:
![]()
Похідна
функції, заданої параметрично.Якщо
функція y=f(x)
задана параметричними рівняннями
![]() ,
тоді похідна визначається за формулою
,
тоді похідна визначається за формулою

Правило
Бернулі-Лопіталя.
Це
правило стосується знаходження границь
частки функцій, якщо границі мають
невизначеності типу![]() в
особливих випадках для розкриття
невизначеності 0;
в
особливих випадках для розкриття
невизначеності 0;
![]() ,
звівши їх до невизначеностей
.
,
звівши їх до невизначеностей
.
Зростання і спадання функції. Екстремуми. Дослідження за допомогою похідної. Асимптоти графіків функцій.
Теорема
1.
Якщо функція
,
диференційована в інтервалі (a;b), неспадна
(незростаюча) на ньому, то її похідна в
цьому інтервалі не від’ємна (не додатна),
тобто
![]() (
(![]() ).
).
Теорема
2.
Якщо функція
,
диференційована в інтервалі (a;b),
задовольняє в ньому умові
![]() (
(![]() ),
то ця функція зростає (спадає) в інтервалі
(a;b).
),
то ця функція зростає (спадає) в інтервалі
(a;b).
Точка
![]() називається точкою
максимуму (мінімуму) функції
,
якщо
називається точкою
максимуму (мінімуму) функції
,
якщо
![]() (
(![]() )
для всіх х, які належать досить малому
околу
.
Максимум і мінімум функції називається
локальними
екстремумами функції,
а відповідні значення аргументу
(локальними) точками екстремуму функції.
)
для всіх х, які належать досить малому
околу
.
Максимум і мінімум функції називається
локальними
екстремумами функції,
а відповідні значення аргументу
(локальними) точками екстремуму функції.
Необхідна
умова екстремуму:
якщо функція
в точці
має екстремум, то похідна
![]() або дорівнює нулю, або не існує.
або дорівнює нулю, або не існує.
Точка , в якій виконується необхідна умова екстремуму, називається критичною точкою.
Достатні умови існування екстремуму в критичній точці:
якщо при переході через критичну точку похідна змінює знак, то точка екстремуму; якщо знак змінюється з плюса на мінус, то точка максимуму, а якщо змінюється з мінуса на плюс, точка мінімуму;
якщо
 ,
то
точка максимуму функції
;
якщо
,
то
точка максимуму функції
;
якщо
 ,
то
точка мінімуму.
,
то
точка мінімуму.
Асимптотою
кривої
називається пряма, до якої необмежено
наближається точка, яка рухається по
кривій, якщо принаймні одна з координат
точки прямує до нескінченності. Іншими
словами, пряма
![]() називається
асимптотою графіка функції
для
називається
асимптотою графіка функції
для![]() ,
якщо різниця
,
якщо різниця
![]()
нескінченно мала для
.
нескінченно мала для
.
Теорема.
Якщо пряма
асимптота графіка функції
для
![]() ,
то
,
то
![]() ,
,
![]() .
.
Якщо
![]() ,
рівняння
визначає похилу асимптоту.
,
рівняння
визначає похилу асимптоту.
Якщо
![]() ,
,![]() асимптота має рівняння
і називається горизонтальною.
асимптота має рівняння
і називається горизонтальною.
Пряма
називається вертикальною
асимптотою графіка
функції
,
якщо хоча б одне з двох граничних значень
![]() ,
,
![]() є нескінченими.
є нескінченими.
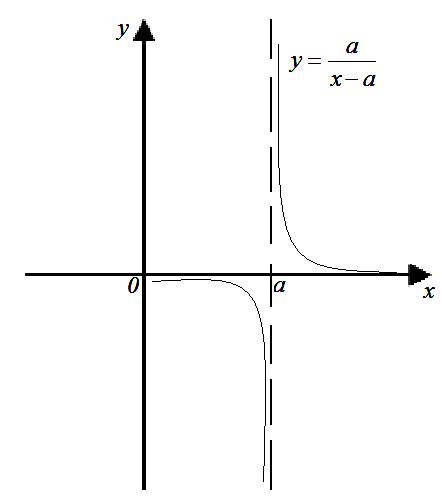
Крива![]() (а>0),
зображена на малюнку має горизонтальну
асимптоту у=0
і
вертикальну асимптоту х=а.
(а>0),
зображена на малюнку має горизонтальну
асимптоту у=0
і
вертикальну асимптоту х=а.
