
- •Алгебраїчна форма комплексного числа. Дії над комплексними числами заданими в алгебраїчній формі.
- •Геометричні задання комплексних чисел. Модуль і аргумент. Тригонометрична і показникові форми комплексного числа.
- •Поняття відсотка, три типи задач на відсотки. Формули простого і складного відсотків.
- •Визначники та їх властивості. Формули Крамера.
- •Векторний і мішаний добуток векторів.
- •Поділ відрізка у даному відношенні. Відстань між двома точками. Полярна система координат.
- •Основні означення і поняття, рівняння еліпса, гіперболи, параболи.
- •Похідні основних елементарних функцій
- •Опуклість та вгнутість. Точки перегину. Дослідження за допомогою похідної.
- •Первісна функція. Невизначений інтеграл. Таблиця невизначених інтегралів. Методи інтегрування.
- •Знакозмінні ряди. Ознака Лейбніца. Абсолютна та умовна збіжність.
- •Функціональні ряди. Степеневий ряд. Область збіжності. Ряд Тейлора і Маклорена.
Основні означення і поняття, рівняння еліпса, гіперболи, параболи.
Еліпс
є геометричне місце точок М
площини,
сума відстаней від кожної з яких до двох
заданих точок
![]() і
і![]() є величина стала.
і
фокуси еліпса;
є величина стала.
і
фокуси еліпса;
![]()
велика вісь;
велика вісь;
![]() - мала вісь ;
- мала вісь ;
![]()
міжфокусна відстань;
міжфокусна відстань;
![]() ;
якщо
;
якщо
![]() фокуси містяться на осі
,
якщо
фокуси містяться на осі
,
якщо
![]() фокуси містяться на осі
.
фокуси містяться на осі
.

Канонічне
(найпростіше) рівняння еліпса: ![]()
Ексцентриситет
еліпса
![]()
це відношення міжфокусної відстані до
великої осі; формули справедливі при
:
це відношення міжфокусної відстані до
великої осі; формули справедливі при
:
![]()
Вираження
половини міжфокусної відстані через
півосі еліпса:
![]()
Фокальні
радіуси-вектори:
![]() ,
,
![]() .
.
Гіпербола
є геометричне місце точок М
площини,
різниця відстаней яких до двох заданих
точок
і
(фокусів), взята за модулем, є величина
стала:
![]()
Гіпербола
перетинає вісь
в
двох точках
![]() ,
які називаються вершинами
гіперболи.
,
які називаються вершинами
гіперболи.
Відрізок
називається дійсною
віссю гіперболи.
Гіпербола має також уявну
вісь,
яка проходить через її центр, але не
перетинає її (пряма
![]() на малюнку)
на малюнку)
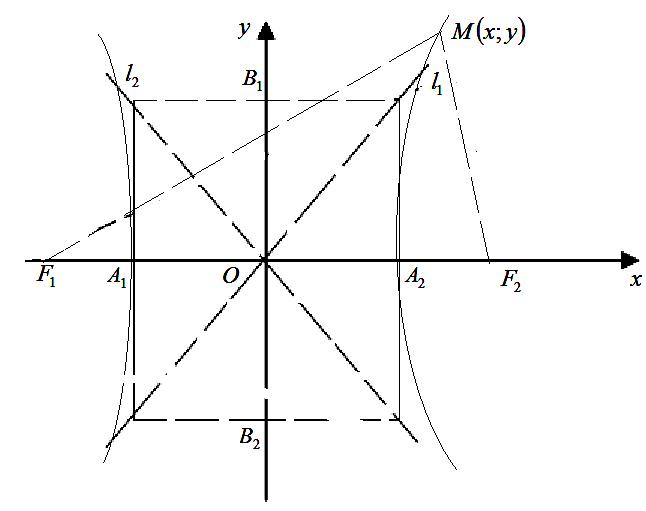
Канонічне
(найпростіше) рівняння гіперболи,
де
![]() ,
відстань між фокусами:
,
відстань між фокусами:
![]()
Ексцентриситет
гіперболи
:
![]() ;
;
![]() ;
;
![]()
Рівняння
асимптот гіперболи
і
:
![]()
Фокальні
радіуси-вектори:
![]() ,
,
![]() .
.
Рівнобічна
гіпербола,
рівняння якої
![]() .
.
Асимптотами
рівнобічної гіперболи
є дві взаємно перпендикулярні прямі
(![]() ).
).
Дві
гіперболи називається спряженими,
якщо вони мають спільний центр О
і спільні осі, але дійсна вісь однієї з
них є уявною віссю іншої.
,
![]()
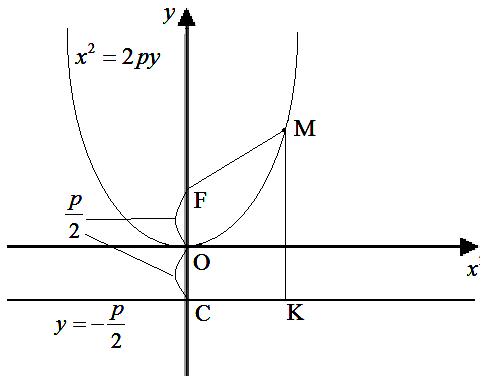
Параболою називається геометричне місце точок М площини, в якої однаково віддалені від заданої точки (фокуса) і заданої прямої (директриса).
O – вершина параболи, М – вершина, яка лежить на параболі, PQ – директриса, MF=MK
Канонічне
рівняння параболи
симетричної відносно осі
:
![]() /
:
/
:
![]()
Фокус
параболи
:
![]() /
:
/
:
![]()
Директриса
параболи
:
![]() /
:
/
:![]()
Фокальний
радіус-вектор параболи
:
![]()
 Оу
Оу 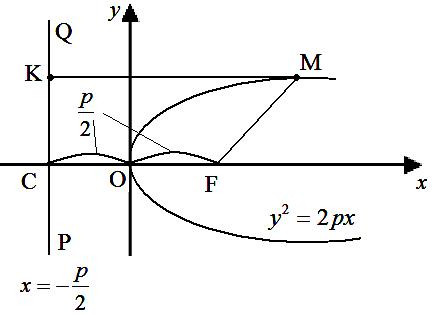 Ох
Ох
Загальне рівняння площини і деякі його випадки. Рівняння площини у відрізках на осях, що проходить через три точки.
Види рівнянь площини.
Координатна
форма рівняння площини, що проходить
через дану точку
![]() і має нормальний вектор
і має нормальний вектор
![]() :
: ![]()
Загальне
рівняння площини:
![]()
Окремі випадки загального рівняння площини:
1)
![]()
рівняння площини, яка проходить через
початок координат.
рівняння площини, яка проходить через
початок координат.
2)
![]()
рівняння площини, паралельної осі
.
рівняння площини, паралельної осі
.
3)
![]()
рівняння площини, паралельної осі
.
рівняння площини, паралельної осі
.
4)
![]()
рівняння площини паралельної осі
рівняння площини паралельної осі
![]() .
.
5)
![]()
рівняння площини, яка проходить через
вісь
.
рівняння площини, яка проходить через
вісь
.
6)
![]()
рівняння площини, яка проходить через
вісь
.
рівняння площини, яка проходить через
вісь
.
7)
![]()
рівняння площини, яка проходить через
вісь
.
рівняння площини, яка проходить через
вісь
.
8)
![]() або
або
![]()
рівняння площини, яка паралельна
координатній
рівняння площини, яка паралельна
координатній
![]() .
.
9)
![]() або
або
![]()
рівняння площини, яка паралельна
координатній
рівняння площини, яка паралельна
координатній
![]() .
.
10)
![]() або
або
![]()
рівняння площини, яка паралельна
координатній
рівняння площини, яка паралельна
координатній
![]() .
.
11)
![]() або
або
![]()
рівняння площини
.
рівняння площини
.
12)
![]() або
або
![]()
рівняння площини
.
рівняння площини
.
13)
![]() або
або
![]()
рівняння площини
.
рівняння площини
.
Рівняння
площини у відрізках на осях координат,
за параметри, які визначають площину,
вибрані відрізки a,
b
i
c,
що відтинаються цією площиною на осях
координат:
![]()
Рівняння
площини, що проходить через три дані
точки
![]() ,
,
![]() ,
,
![]() :
:

Різні види рівнянь прямої у просторі: загальне, канонічне, параметричне, через дві точки.
Види рівнянь у просторі.
Загальне
рівняння прямої у просторі:
![]()
Канонічне
рівняння прямої, яка проходить через
точку
![]() ;
х, у, z – координати точки М
на цій прямій; m,
n,
р – координати напрямленого вектора
прямої, тобто
;
х, у, z – координати точки М
на цій прямій; m,
n,
р – координати напрямленого вектора
прямої, тобто
![]() :
:
![]() .
.
Параметричне
рівняння прямої;
![]() - координати точки
- координати точки
![]() ,
що лежить на прямій; t
– параметр:
,
що лежить на прямій; t
– параметр:

Рівняння
прямої, що проходить через дві дані
точки
![]() і
:
і
:
![]()
Графічні методи розв’язання задач лінійного програмування. Алгоритм графічного методу.
Для розв’язання двовимірних задач лінійного програмування, тобто задач з двома змінними, а також тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування.
Розглянемо таку задачу.
Знайти екстремум (мінімум, максимум) функції:
![]() - цільова
функція
- цільова
функція
за умов

Припустимо, що система за умов сумісна і многокутник її розв’язків обмежений.
Згідно з геометричною інтерпретацією задачі лінійного програмування кожне і-те обмеження-нерівність визначає півплощину з граничною прямою. Системою обмежень описується переріз усіх зазначених півплощин, координати яких задовольняють всі обмеження задачі. Таку множину точок називають многокутником розв’язків, або областю допустимих планів (розв’язків) задачі лінійного програмування.
Умова
невід’ємності змінних означає, що
область допустимих розв’язків задачі
належить першому квадрату системи
координат двовимірного простору. Цільова
функція задачі лінійного програмування
геометрично інтерпретується як сім’я
паралельних прямих
![]() .
.
Сформулюємо деякі властивості задачі лінійного програмування, застосовані під час її графічного розв’язання.
Якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин многокутника розв’язків. А якщо цільова функція досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин.
Отже, розв’язати задачу лінійного програмування графічно означає знайти таку вершину многокутника розв’язків, у результаті підставляння координат якої в лінійну цільову функцію, вона набуває найбільшого (найменшого) значення.
Алгоритм графічного методу розв’язання задач лінійного програмування:
Будуємо прямі лінії, рівняння яких дістаємо заміною в обмеженнях задачі знаків нерівностей на знаки рівностей.
Визначаємо півплощини, що відповідають кожному обмеженню задачі.
Знаходимо многокутник розв’язків задачі лінійного програмування.
Будуємо вектор
 ,
що задає напрям зростання значень
цільової функції задачі.
,
що задає напрям зростання значень
цільової функції задачі.Будуємо пряму , перпендикулярну до вектора
 .
.Переміщуючи пряму в напрямі вектора (для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину многокутника розв’язків, де цільова функція досягає екстремального значення.
Визначаємо координати точки, в якій цільова функція набуває максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.
Постановка транспортної задачі.
Транспортна задача – це специфічна задача лінійного програмування застосована для визначення най економнішого плану перевезення однорідної продукції від постачальників до споживачів.
Математична модель транспортної задачі.
![]() (1)
(1)
за обмежень
![]()
![]()
![]() ,
,
де
![]()
кількість продукції, що перевозиться
від і-го постачальника до j-го споживача,
кількість продукції, що перевозиться
від і-го постачальника до j-го споживача,
![]()
вартість перевезення одиниці продукції
від і-го постачальника до j-го споживача;
вартість перевезення одиниці продукції
від і-го постачальника до j-го споживача;
![]()
запаси продукції і-го постачальника;
запаси продукції і-го постачальника;
![]()
попит на продукцію j-го споживача.
попит на продукцію j-го споживача.
Якщо в
транспортній задачі загальна кількість
продукції постачальників дорівнює
загальному попиту всіх споживачів тобто
![]() ,
то таку транспортну задачу називається
збалансованою або закритою. Якщо ж така
умова не виконується, то транспортну
задачу називається незбалансованою,
або відкритою.
,
то таку транспортну задачу називається
збалансованою або закритою. Якщо ж така
умова не виконується, то транспортну
задачу називається незбалансованою,
або відкритою.
Оптимальним
планом транспортної задачі
називають матрицю
![]() ,
яка задовольняє умови задачі і для якої
цільова функція (1) набуває найменшого
значення.
,
яка задовольняє умови задачі і для якої
цільова функція (1) набуває найменшого
значення.
Алгоритм методу потенціалів складається з таких етапів.
Визначення типу транспортної задачі (відкрита чи закрита).
Побудова першого опорного плану транспортної задачі.
Перевірка плану транспортної задачі на оптимальність.
Якщо умова оптимальності виконується, то маємо оптимальний розв’язок транспортної задачі. Якщо ж умова оптимальності не виконується, необхідно перейти до наступного опорного плану.
Новий план знову перевіряють на оптимальність, тобто повторюють дії п. 3) і т.д.
Означення, область визначення, область значень, способи задання функції. Властивості функції: парність і непарність, періодичність, зростання і спадання.
Означення.
Якщо кожному елементу x із множини Х
поставити у відповідність єдиний елемент
у із множини У, то кажуть, що на множині
Х задана функція, що символічно записують
![]() .
.
Змінну х при цьому називають незалежною змінною або аргументом, а змінну у залежною змінною або функцією.
Множина
всіх допустимих значень незалежної
змінної утворює область
визначення функції
,
яку позначають
![]() або
або
![]() .
.
Множина
відповідних значень залежної змінної
у, яких вона набуває при всіх значеннях
з області визначення функції називається
областю
значень,
яку позначають
![]() або
або
![]() .
.
Способи задання функцій:
графічний (множиною точок координатної площини);
табличний (функція задається таблицею);
аналітичний (задається формулою);
область визначення.
Властивості функцій, визначених на симетричному відносно початку числової осі проміжку. Парні і непарні функції.
Нехай функція визначена на симетричній відносно точки О числової осі множині. Тоді:
функція називається парною, якщо
 ;
;функція називається непарною, якщо
 .
.
Графік парної функції симетричний відносно осі Оу, а графік непарної функції симетричний відносно початку координат.
Існують
функції, що не належать ні
до парних, ні до непарних,
але будь-яку функцію
![]() можна представити у вигляді суми парної
і непарної функцій, тобто
можна представити у вигляді суми парної
і непарної функцій, тобто
![]() ,
де
,
де
![]()
парна функція,
парна функція,
![]()
непарна функція.
непарна функція.
Властивості парних і непарних функцій:
сума, різниця, добуток і частка двох парних функцій є парна функція;
сума, різниця непарних функцій є непарна функція, а добуток і частка – парна функція;
добуток і частка двох функцій різної парності є функція непарна.
Функція
,
яка визначена на симетричній нескінченній
множині називається періодичною,
якщо існує таке число
![]() ,
що при всіх значеннях х з області
визначення число
,
що при всіх значеннях х з області
визначення число
![]() також належить області визначення і
виконується рівність:
також належить області визначення і
виконується рівність:
![]() .
.
Число
Т називається періодом
функції
,
а найменше додатне число
![]() ,
якщо має цю властивість, називається
оновленим періодом функції
.
Якщо Т – період функції
,
то
,
якщо має цю властивість, називається
оновленим періодом функції
.
Якщо Т – період функції
,
то
![]()
![]() також є періодом функції:
також є періодом функції:
![]() .
.
Функцію
називають зростаючою
(спадною)
в інтервалі (a;b), якщо для будь-яких
значень
і
з цього інтервалу з нерівності
![]() випливає нерівність
випливає нерівність
![]() (відповідно
(відповідно
![]() ).
Якщо ж для таких
і
з нерівності випливає нерівність
(відповідно
).
Якщо ж для таких
і
з нерівності випливає нерівність
(відповідно
![]() ),
то функцію
називають неспадною
(незростаючою)
в інтервалі (a;b).
),
то функцію
називають неспадною
(незростаючою)
в інтервалі (a;b).
Функції всіх цих типів називаються монотонними.
Елементарні функції та їх властивості.
Лінійною
називається функція виду![]() ,
де
,
де
![]() .
.
Властивості:
Область визначення – R, тобто
 .
.Область значень – R.
Парність: якщо

функція ні парною, ні непарною (загального
вигляду); якщо
функція ні парною, ні непарною (загального
вигляду); якщо

функція парна; якщо
функція парна; якщо

функція непарна; якщо
функція непарна; якщо

функція і парна, і непарна.
функція і парна, і непарна.Монотонність:

зростаюча;
зростаюча;

спадна;
спадна;

стала.
стала.Періодичність: неперіодична при
 ,
періодична з будь-яким періодом.
,
періодична з будь-яким періодом.Графік: пряма лінія
![]()
Степеневою
називається
функція
![]() ,
де а
– будь-яка дійсна стала.
,
де а
– будь-яка дійсна стала.
Властивості:
![]() ,
де
,
де
![]()
Область визначення – R.
Область значень – R, якщо n непарне;
 ,
якщо n
парне.
,
якщо n
парне.Парність: непарна, якщо n непарне число; парна, якщо n парне число.
Монотонність: якщо n парне число, то функція спадає на проміжку
 і зростає на проміжку
і зростає на проміжку ;
якщо n
непарне число, то функція зростає на
множині R.
;
якщо n
непарне число, то функція зростає на
множині R.Періодичність: неперіодична.
Графік: парабола
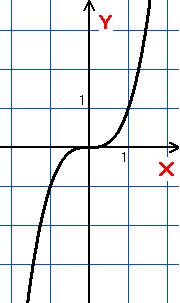
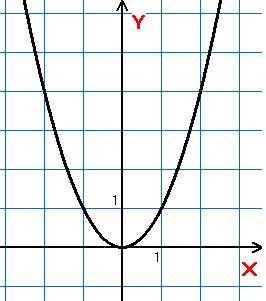
n непарне n парне
![]() ,
де
,
де
Область визначення –
 .
.Область значень –
 ,
якщо n
непарне число;
,
якщо n
непарне число;
 n
парне число.
n
парне число.Парність: непарна, якщо n непарне число; парна, якщо n парне число.
Монотонність: якщо n парне число, то функція зростає на проміжку
 і спадає на проміжку
і спадає на проміжку ;
якщо n
непарне число, то функція спадає на
проміжку
;
якщо n
непарне число, то функція спадає на
проміжку
 .
.Періодичність: неперіодична при , періодична з будь-яким періодом.
Графік:
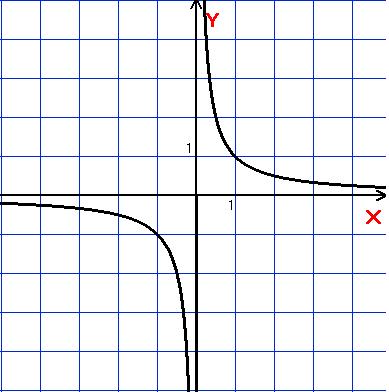
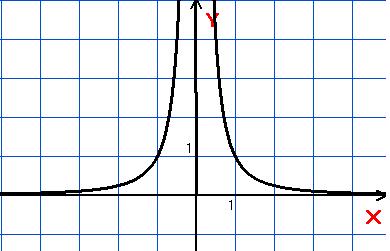
n непарне n парне
![]() ,
де
,
де
Область визначення –
 ,
якщо n
парне число;
,
якщо n
парне число;
 ,
якщо n
непарне число.
,
якщо n
непарне число.Область значень –
 ,
якщо n
парне число;
,
якщо n
парне число;
 ,
якщо n
непарне число.
,
якщо n
непарне число.Парність: непарна, якщо n непарне число; загального вигляду (ні парна, ні непарна), якщо n парне число.
Монотонність: якщо n парне число, то функція зростає на проміжку ;якщо n непарне число, то функція зростає на проміжку
 .
.Періодичність: неперіодична.
Графік:
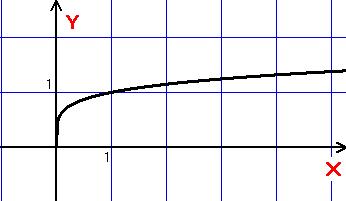
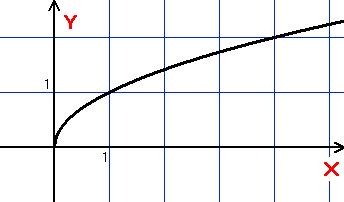
n непарне n парне
Показниковою
називається функція
![]() ,
якщо
,
якщо
![]() .
.
Властивості:
Область визначення – R.
Область значень – .
Парність: функція не є ні парною, ні непарною (загального вигляду).
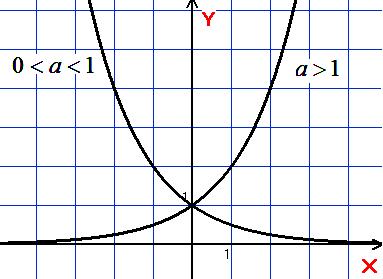
Монотонність: якщо

зростаюча на множині R;
якщо
зростаюча на множині R;
якщо
спадна на множині
R.
спадна на множині
R.Періодичність: неперіодична.
Графік:
Логарифмічною
називається
функція
![]() ,
якщо
.
,
якщо
.
Властивості:
Область визначення – .
Область значень – R.
Парність: функція не є ні парною, ні непарною (загального вигляду).
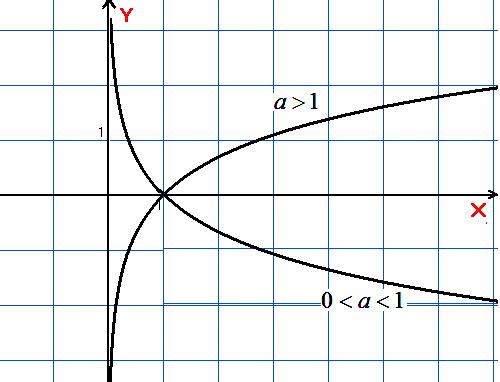
Монотонність: якщо зростаюча на всій області визначення
 ;
якщо
;
якщо
спадна на всій області визначення
.
спадна на всій області визначення
.Періодичність: неперіодична.
Графік:
Тригонометричними
називаються функції
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Властивості:
Область визначення – R;
 .
.Область значень –
 .
.Парність: непарна.
Монотонність: зростаюча на проміжку
 ;
спадна на проміжках
;
спадна на проміжках
 .
.Періодичність: періодична;
 ;
;
 .
.Графік:
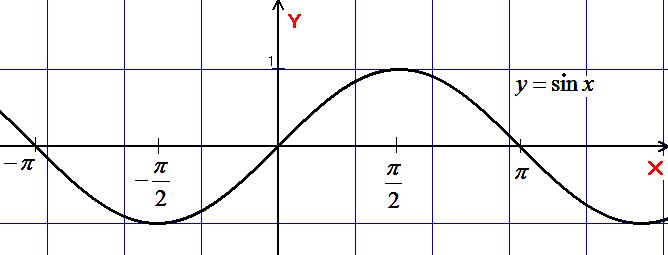
Область визначення – R.
Область значень – .
Парність: парна.
Монотонність: зростаюча на проміжках
 ;
спадна на проміжках
;
спадна на проміжках
 .
.Періодичність: періодична; ; .
Графік:
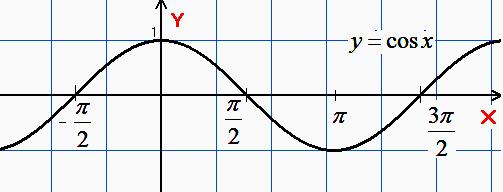
Область визначення –
 .
.Область значень – R.
Парність: непарна.
Монотонність: зростаюча.
Періодичність: періодична; ; .
Графік:
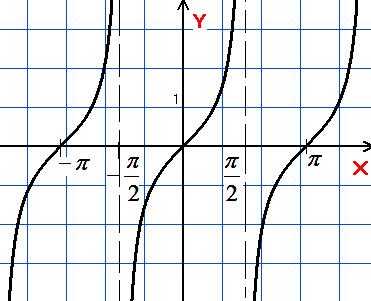
Область визначення –
 .
.Область значень – R.
Парність: непарна.
Монотонність: спадна.
Періодичність: періодична; ; .
Графік:
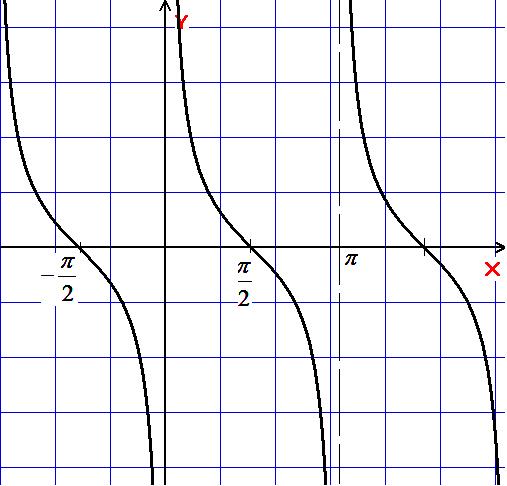
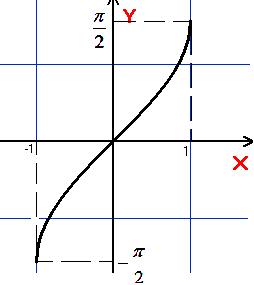
Оберненими
тригонометричними
називаються функції![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Вони є оберненими до функцій
,
,
,
.
Вони є оберненими до функцій
,
,
,
Властивості:
Область визначення –
 .
.Область значень –
 .
.Парність: непарна.
Монотонність: зростаюча.
Періодичність: неперіодична
Графік:
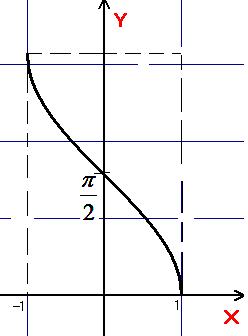
Область визначення – .
Область значень –
 .
.Парність: непарна.
Монотонність: спадна.
Періодичність: неперіодична
Графік:
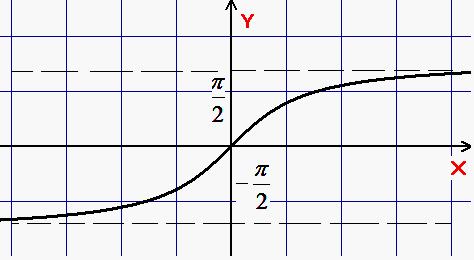
Область визначення –
 .
.Область значень – .
Парність: непарна.
Монотонність: зростаюча.
Періодичність: неперіодична
Графік:
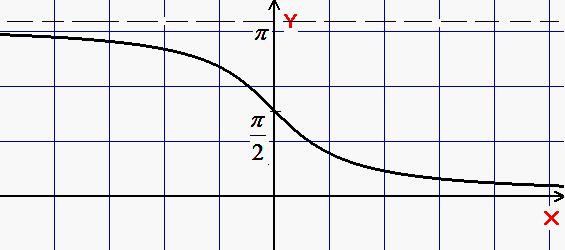
Область визначення – .
Область значень – .
Парність: функція не є ні парною, ні непарна.
Монотонність: спадна.
Періодичність:
Графік:
Неперервність функції. Розрив функції. Перша і друга чудові границі.
Функція
називається неперервною
в точці
,
якщо вона визначена в точці
![]() і її околі, і існує границя функції
для
і її околі, і існує границя функції
для
![]() ,
яка дорівнює значенню функції в точці
:
,
яка дорівнює значенню функції в точці
:
![]() .
.
Функція
називається неперервною
на відрізку
![]() ,
якщо вона неперервна в кожній точці
інтервалу
,
якщо вона неперервна в кожній точці
інтервалу
![]() ,
а в точках
,
а в точках
![]()
неперервна відповідно справа і зліва:
неперервна відповідно справа і зліва:
![]()
![]()
Розриви функції.
Функція має розрив в точці , якщо вона не є неперервною в цій точці. Розрізняють два головних види розривів – розрив першого й другого родів.
Розрив
першого роду.
Кажуть, що в точці
![]() функція
має розрив першого роду, якщо однобічні
границі існують і задовольняють одній
з двох умов:
функція
має розрив першого роду, якщо однобічні
границі існують і задовольняють одній
з двох умов:
однобічні границі співпадають між собою, але не співпадають із значенням функції в точці , тобто
![]()
однобічні границі не співпадають, тобто
![]()
Умова (1) визначає розрив, що називається усувним розривом.
Умова
(2) визначає розрив, що називається
стрибком,
причому число![]() називається величиною стрибка.
називається величиною стрибка.
Розрив другого роду. Функція в точці має розрив другого роду, якщо принаймні одна з однобічні границь дорівнює нескінченності або не існує.
Наприклад,
функція
![]() має в точці
розрив другого роду. Всі дробові функції,
знаменник яких при
дорівнює 0, а чисельник не дорівнює 0,
мають для
розрив другого роду.
має в точці
розрив другого роду. Всі дробові функції,
знаменник яких при
дорівнює 0, а чисельник не дорівнює 0,
мають для
розрив другого роду.
Перша
чудова границя
![]()
Друга
чудова границя
![]()
Перетворення графіків функцій.
Задано функція
1)
![]()
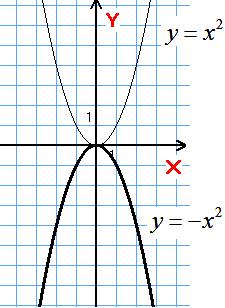
Симетрія відносно осі
2)
![]()
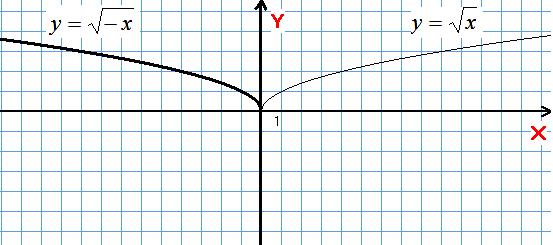
Симетрія відносно осі
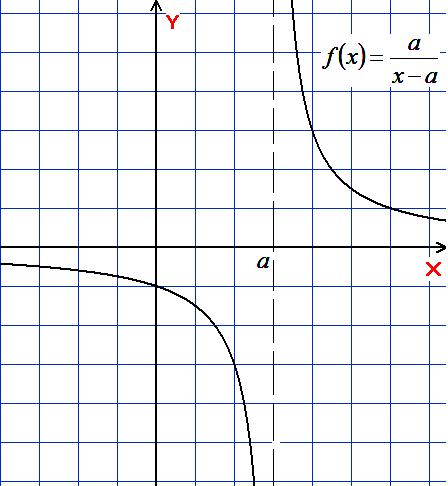
3)
![]()
Вище від осі ( і на самій осі) – без змін, нижче від осі симетрія відносно осі .
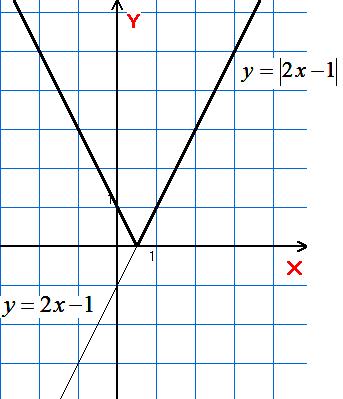
4)
![]()
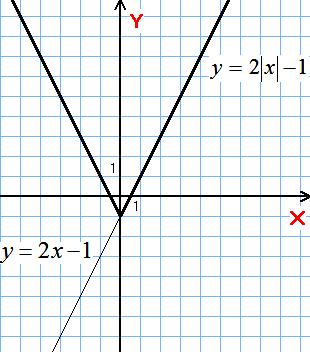
Праворуч від осі ( і на самій осі) – без зміни і ця ж сама частина симетрія відносно осі .
5)
![]()
![]()
6)
![]()
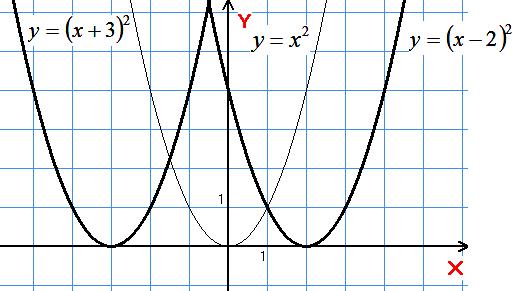
Паралельне перенесення вздовж осі на а одиниць.
7)
![]()
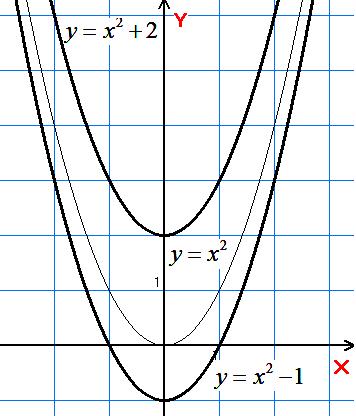
Паралельне перенесення вздовж осі на а одиниць.
8)
![]() ,
,
![]()
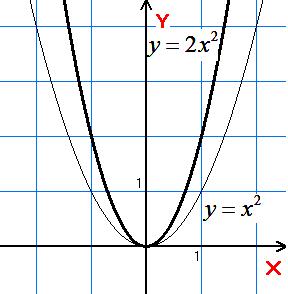
Той
самий вигляд, що й у графіку
,
тільки розгорнуто, або стиснуто вздовж
осі
(при
![]() розгорнуто, при
стиснуто).
розгорнуто, при
стиснуто).
9)
![]() ,
,
![]()
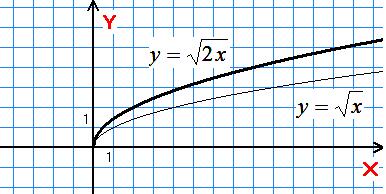
Той
самий вигляд, що й у графіка
,
тільки розгорнуто, або стиснуто вздовж
осі
(при
![]() стиснуто, при
розгорнуто).
стиснуто, при
розгорнуто).
Означення похідної. Таблиця похідних. Правила диференціювання. Похідна складеної функції.
Похідною
функції y=f(x)
в
точці х
називається границя відношення приросту
функції
![]() в точці х до приросту аргументу
в точці х до приросту аргументу
![]() ,
коли приріст аргументу прямує до нуля,
якщо ця границя існує.
,
коли приріст аргументу прямує до нуля,
якщо ця границя існує.
![]()
