9. Векторний і мішаний добуток векторів.

Векторним добутком вектора на вектор називається вектор , довжина якого чисельно дорівнює площі паралелограма, побудованого на векторах і , перпендикулярний до площини цих векторів і напрямлений так що вектори , , утворюють праву трійку. Способи позначення векторного добутку:

Довжина вектора, який є векторним добутком векторів і

Обчислення векторного добутку

Векторний добуток векторів і , заданих координатами

Векторний добуток векторів і , записаний за допомогою визначників другого порядку

Векторний добуток векторів і , записаний за допомогою визначників третього порядку

Мішаним добутком трьох векторів , і називається число, яке дорівнює векторному добутку , помноженому скалярно на вектор .

або

Способи позначення мішаного добутку:

Обчислення мішаного добутку

Мішаний добуток трьох векторів дорівнює визначнику, складеному з координат цих векторів: , ,

10. Поділ відрізка у даному відношенні. Відстань між двома точками. Полярна система координат.

Відстань між двома точками А(x₁, y₁) і B (x₂, y₂) на площині Оxy

Точка М (х; у) лежить на відрізку М₁М₂ і поділяє його у відношені , ,

Визначення координат точки М через координати точок М₁(x₁, y₁) і М₂ (x₂, y₂)

,

Координати середини відрізка (при )

;

Полярна система координат – задається полюсом і полярною віссю

М (; )

Кут має знак «+», якщо проти годинникової стрілки, « - »  за годинниковою стрілкою

Зв’язок між полярними і прямокутними координатами.

Формули переходу від полярних до прямокутних координат

Формули переходу від прямокутних до полярних координат

11. Різні види рівнянь прямої на площині: канонічне, параметричне, з кутовим коефіцієнтом, загальне, через дві точки , у відрізках на осях. Взаємне розміщення прямих на площині. Відстань від точки до прямої.

Види рівнянь прямої на площині.

Канонічне рівняння прямої; х, у – координати довільної точки прямої; х₀, у₀ – координати даної точки, через яку проходить ця пряма; m, n – координати напрямленого вектора прямої:

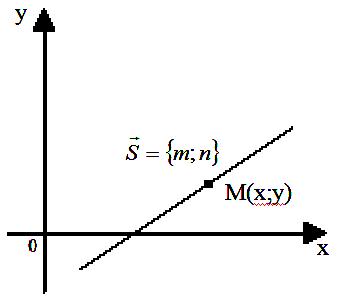
Параметричне рівняння прямої; t – параметр.

Рівняння прямої з кутовим коефіцієнтом k; ,  кут, який утворює пряма з додатнім напрямком осі ; b – відрізок, що відтинається прямою на осі .

Рівняння прямої, яка проходить через дану точку (рівняння пучка прямих); k – кутовий коефіцієнт прямої.

Рівняння прямої, що проходить через дві дані точки та

Загальне рівняння прямої на площині ху: А, В – координати вектора, нормального до даної прямої .

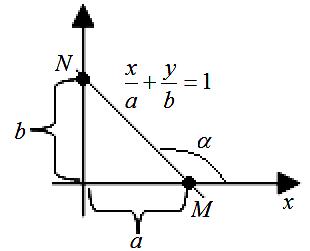
Рівняння прямої у відрізках на осях координат; точки  відповідно точки перетину прямої з осями координат.

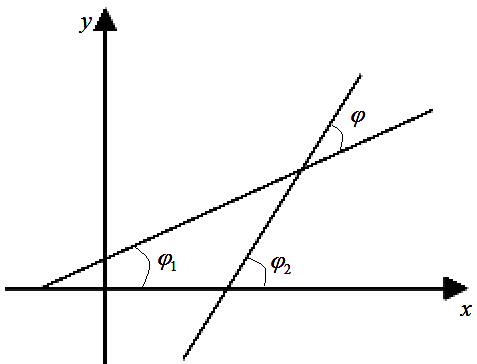
Формула для обчислення кута між не перпендикулярними прямими заданими рівнянням , , ,

Умова паралельності прямих і , заданих рівнянням з кутовим коефіцієнтом: , ; :

Умова перпендикулярності прямих і , заданих рівнянням з кутовим коефіцієнтом: , ; :

Відстань d від точки до прямої, якщо пряма задана загальним рівнянням :