1. Поняття множини. Дії з множинами. Числові множини.

Множина  це сукупність елементів, що мають певну властивість. Позначають великими латинськими літерами (A, B, C, X, Y, …), а елементи малими латинськими літерами (a, a₁ …). Елементи множини  об’єкти, з яких складаєть множина.

Той факт, що об’єкт а є елементом множини М записується так: .Знак називається знаком належності( -неналежить).

Задання множин:

1сп.: у фігурних дужках { 2, 3, 7}

2сп.: предикатний спосіб { x| x- непарні, ціні числа}

Числові множини:

N  натуральні числа (це числа, якими користуються при лічбі предметів)

Z  цілі числа (це натуральні числа та їм протилежні числа, і нуль)

Q  раціональні числа (це числа, які можна подати у вигляді дробу )

I  ірраціональні числа (це нескінченні, неперіодичні числа : )

R  дійсні числа (раціональні та ірраціональні числа)

C  комплексні числа

Потужність кількість елементів, позначається |A|.

Порожня множина – це множина, яка не містить жодного елемента, позначається .

Універсум (U, E)  множина допустимих об’єктів.

Дії над множинами:

Об’єднанням множини А і В називається множина тих елементів, які належать хоча б одній із цих множин.

Перетином множини А і В називається множина , що складається з елементів, які належать множинам А і В одночасно. .

Доповненням множини А (яка є підмножиною універсальної множини Е) – називається множина всіх елементів універсальної множини, які не належать множині А. , .

Доповненням множини А до множини В називається така множина всі елементи якої належать В, неналежать множині А. , .

Різницею множин А і В називається множина тих елементів, які належать множині А і неналежать множині В.

Симетричною різницею множин А і В називається множина, яка складається з усіх елементів множини А, які не містяться в множині В, а також усіх елементів множини В, які не містяться в множині А.

2. Алгебраїчна форма комплексного числа. Дії над комплексними числами заданими в алгебраїчній формі.

Комплексним числом називається число вигляду , в якому , а і- символ, що задовольняє умова . Символ «і» називається уявною одиницею, число х називається дійсною частиною комплексного числа z, а число у – уявною частиною комплексного числа. Для цих чисел прийняті позначення : ;

Поняття «менше» і «більше» для комплексних чисел не визначено. Запис означає, що число не дорівнює числу .

Комплексне число називають спряженим до комплексного числа . Взагалі, два комплексних числа, які відрізняються тільки знаком при уявній частині, називаються комплексно-спряженими.

Два комплексні числа і вважаються рівними між собою, якщо відповідно рівні їхні дійсні і уявні частини, тобто .

Комплексне число називається нулем і позначається 0.

Дії над комплексними числами заданими в алгебраїчній формі:

Сумою двох комплексних чисел заданих в алгебраїчній формі називається комплексне число дійсна частина, якого дорівнює сумі дійсних частин даних чисел, а уявна – сумі уявних.

Аналогічно віднімаються.

Добуток виконується як двочлен на двочлен враховуючи, що .

Щоб поділити комплексні числа в алгебраїчній формі чисельник і знаменник домножають на число спряжене до знаменника.

3. Геометричні задання комплексних чисел. Модуль і аргумент. Тригонометрична і показникові форми комплексного числа.

Геометричне зображення комплексного числа.

Комплексне число визначається парою дійсних чисел і може бути зображене геометрично на площині точкою або її радіусом-вектором , проекції якого на осі і дорівнюють і . При цьому координатна площина називається комплексною площиною, вісь абсцис – уявною віссю, вісь ординат – уявною віссю комплексної площини.

Відстань від точки до центра координат називається модулем комплексного числа:

Аргументом комплексного числа називається кут , який утворює радіус-вектор точки з додатнім напрямом осі .

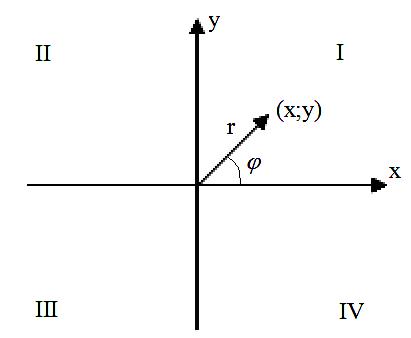
Алгоритм знаходження аргументу:

1) Знаходимо початковий кут : ;

2) За знаком х та у визначаємо чверть, в якому лежить комплексне число:

І: II: III: IV:

- тригонометрична форма комплексного числа.

Множення, ділення і піднесення до степеня комплексних чисел значно спрощується, якщо подати їх у тригонометричній формі.

При множенні комплексних чисел у тригонометричній формі їхні модулі перемножаються, а аргументи додаються.

При діленні комплексних чисел у тригонометричній формі їхні модулі діляться, а аргументи віднімаються.

Піднесення до степеня: ;

Формула Муавра:

Корінь степеня і з комплексного числа визначається як комплексне число z, n-ий степінь якого дорівнює даному числу , тобто .

Формула Ейлера:

- показникові форма комплексного числа

Аналогічно до тригонометричної форми виконуються дії множення, ділення, піднесення до степеня.

4. Поняття відсотка, три типи задач на відсотки. Формули простого і складного відсотків.

Відсотком від числа А називається одна сота частина цього числа:

Для того щоб знайти відсотковий вираз заданого числа (цілого чи десяткового дробу), достатньо помножити це число на 100.

Для того щоб знайти число за його відсотковим виразом, достатньо поділити вираз на 100.

Три основні задачі на відсотки.

Задача 1. Знайти певний відсоток заданого числа. Задане число ділиться на 100 і множиться на відповідне число відсотків.

Задача 2. Знайти число за відомим значенням певного його відсотка. Задане значення відсотка (відому частину числа) шуканого числа ділимо на число, що виражає цей відсоток, а результат множимо на цей відсоток.

Задача 3. Знайти вираз одного числа у відсотках іншого (так зване відсоткове відношення двох чисел). Ділимо одне число на інше (знаходимо їх відношення) і результат множимо на 100.

Формула простого відсотка.

Відношення даного відсотка певного числа (скажімо, грошової суми) до самого цього числа називається відсотковою ставкою і позначається р. питомою відсотковою ставкою (нормою відсотка) називається відношення .

Якщо певний відсоток деякої грошової суми додається до цієї суми, то говорять про накопичення грошей. Якщо відсоток не нараховується на перший відсоток, що досягає до початкового числа, говорять про простий відсоток.

Формула приросту простого відсотка.

Сума, яку буде накопичувано з урахуванням простих відсотків за n років: , де К – початкове число; і – питома відсоткова ставка (норма відсотка); К_ni – прості відсотки за n років.

Якщо відсоток початкового числа додається до цього числа, а далі відсоток нараховується на утворену суму, тобто на більше число, то говорять про складні відсотки.

Формула складного відсотка.

Нехай на початкове число К нараховується складний відсоток за певною нормою протягом n років. Тоді дістанемо таку послідовність сум:

після 1-го року: ;

після 2-го року: ;

після n-го року:

Основна формула складного відсотка.

Якщо складний відсоток нараховується протягом n років, виконується така залежність:

Вираз називається коефіцієнтом складного відсотка.

Обчислення початкової суми за відомим її кінцевим значенням називається дисконуванням. Різниця D між кінцевою сумою та сумою К, що дисконується, називається дисконтом: .

Якщо грошові кошти вкладати під прості відсотки на n років за питомої відсоткової ставки і, то остаточна сума буде така: . Отже, дисконтовані грошові кошти становитимуть: . У разі складних відсотків маємо: , а дисконтоване значення грошової суми: . Коефіцієнт називається коефіцієнтом дисконту.