6.Avl ағашта сол жақ және оң жақ бұрылыс операциялары.

Aлдымен бұрын тұрғызылған AVL ағашына жаңа төбелі қабырғаны жалғау ағаштың баланссыздығына әкеліп соғатынын ескерейік ж/е керісінше қабырғамен сәйкес төбемен бастапқы ағаштың қосу нүктесі болатын боялмаған төбе/ді жалғауда балансыздану болмайды.

1-сурет

Төбе қасындағы цифра осы төбенің балансы мәні.

AVL ағашқа жаңа төбе қосу кезінде бинарлы ағашты тұрғызудың қарапайым алгоритмі қолданылады. Осылайша, бар болған AVL ағашқа қайта қосылған төбе, оны N арқылы белгілейік, ағаш түбірі мен жаңа төбені қосатын ерекшеленген деп аталатын жол үшін ақырғы төбе болып табылады.

AVL ағашқа жаңа төбелер қосу есебі шешімін корректі түрде жүргізетін жалпы талаптарға тоқталып кетейік:

1. Осы түрлендіру нәтижесінде алынған бинарлы ағаш іздеудің бинарлы ағашы болу керек;

2. Нәтижелік ағаш AVL ағашы болуы керек;

3. Түрлендіру жеткілікті түрде тиімді болуы керек.

Осыған байланысты, жаңа төбе қосқанға дейін AVL ағашы болған, бірақ балансы жаңа төбе қосу нәтижесінде бұзылған ағаштың ішкі ағаштарымен орындалатын екі операцияны қарастырайық. Қажет болған жағдайда бұл операциялар кез-келген бинарлы іздеу ағашымен жүргізіле алады.

Алғашқы операция сол жақ бұрылыс, мағынасын келесі сурет ұғындырады.

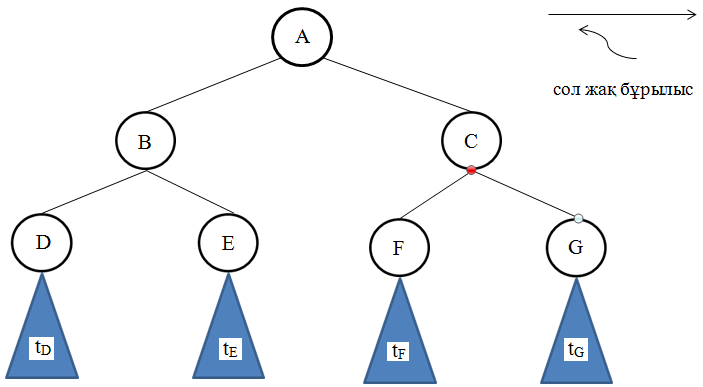
2-сурет

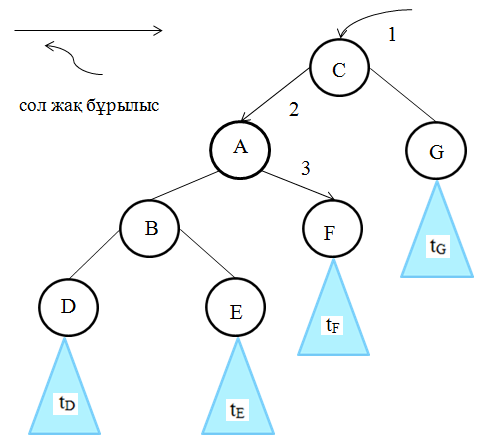
3-сурет

3 суретіндегі ағашты айналуда түйіндердің тізбегі симметриялы түрде сол қалыпында бастапқы ағаш 3 суреттегідей болады.

Сонда t_D={D}; t_E={E}; t_F={F}; t_G={G} шарты ушін бұл тізім D,B,E,A,F,C,G болады.

Осыған ұқсас ағашты оң жақ бұрылыс кезінде төмендегі суреттегідей орындалады.

4-сурет

Сонымен бинарлы іздеу ағашымен сол жақ немесе оң жақ бұрылыс операциясын орындау нәтижесінде алынған ағаш бинарлы іздеу ағашы болып қалады. Ескерте кетсек, сол жақ немесе оң жақ бұрылыс операциясын орындау онша қиын шаруа емес, себебі олардың әрбірін орындағанда тек үш сілтемені ғана қайта баптау керек және ең маңыздысы бұл t_D, t_E, t_F,t_G ішкі ағаштарынан тәуелсіз жүргізіледі. Егер жоғарыда келтірілген бұрылыстар схемасы түсініксіз болса, онда осыны қарапайым схемалар үшін қайталауға болады, мысалы, үш төбе мен 4-ші ішкі ағаш 5 сурет және 6 сурет.

Формальды түрде басқа жолдардың төбелерінің балансы да өзгеруі мүмкін, тек бұл жолдардың ішіндегі төбелер бір уақытта ерекшеленген жол төбелері болғанда ғана болады.

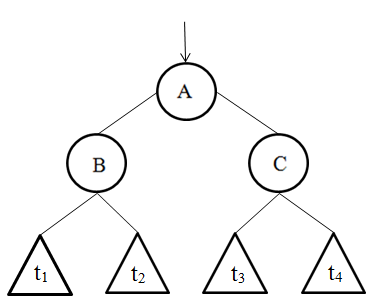
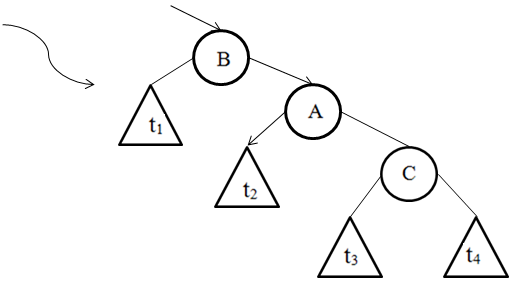
5-сурет

А төбесіндегі түбірлі ішкі ағаштың оң жақ бұрылысы

А төбесіндегі түбірлі ішкі ағаштың сол жақ бұрылысы

6-сурет

Әрине екі төбесі мен үш ішкі ағашы бар ағаштар үшін қарапайым бұрылыстар жасауға болады.

7-сурет

7. Ықтималды іздеу ағашы.

Массив элементтері үлестірілген ықтималдыққа сәйкес кездейсоқ тізбектеп қарастырылсын. Бұл жағдайда бинарлы іздеу ағашын құру стратегиясының басты идеясы мынада: массив элементінің қарастырылу ықтималдығы ең үлкен болғаны, ағаштың жоғарғы ярустарында түбірге жақын орналасады. Ықтималдығы кіші болған элементтер ағаш түбірінен алыстап, төменгі ярустарда бекітіледі. Осы стратегияға сүйеніп, құрылған ағаш бойында массив элементін іздеу кезінде, іздеу уақыты үнемделеді. Ағашты құру процесінде ішкі ағаштарды сол жақ және оң жақ бұруды қолданады. Мұндай ағаштарды әдетте ықтималды бинарлы іздеу ағашы деп атау орынды. Берілген мәнді төбенің қарастырылу ықтималдығы туралы ақпаратқа осы төбе ерекшеленген жолдың соңында өзінің алдын ала орнын алғаннан кейін ғана қол жеткізуге болады деп есептейміз. Егер төбенің қарастырылу ықтималдығы осы төбенің таңдама пайда болу мезетінде, яғни мәнімен бір уақытта, қол жетімді болса, онда ықтималдық ағашын тұрғызу себебі қарапайым шешімге ие болады.

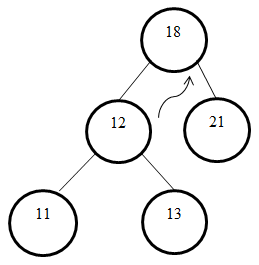
Мысал ретінде массив бөлігі негізінде құрылған ағашты қарастырайық. Бұл ағашта кезекті қадамда пайда болу ықтималдығы 0,085 және мәні 12 тең жаңа төбе қосылған болсын.

7.1-сурет

Жаңа төбені қосу алгоритмі негізінде ықтималдығы 0,085, ал мәні 12 тең элементтің өз деңгейі мен өз орнында емес, басқа яруста орналасатыны айқын. Оны өз орнына орнату үшін түбірі 11-ге тең ішкі ағашты сол жақ бұруды орындау қажет. Бұдан түбір 13 болатын жаңа ішкі ағаш аламыз.

7.2-сурет

Келесі қадамда осы ағашқа оң жақ бұруды, түбірі 18 тең ішкі ағашқа да оң жақ бұруды орындау қажет. Содан кейін түбірі мәні 10 тең түйіндегі ішкі ағашқа сол жақ бұруды, соңғының алдындағы және соңғы қадамды орындау қажет.

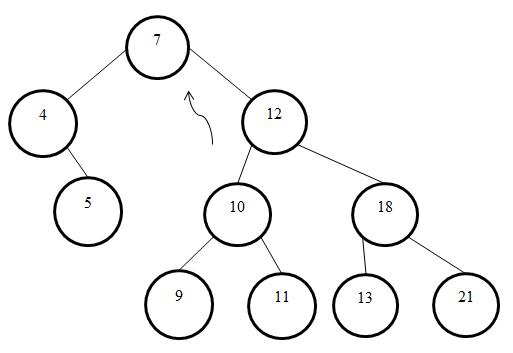
7.3-сурет

7.4-сурет

Құру алгоритмі күрделі емес. Әр қадамда қарастырылған төбенің ағаш бойында орналасуына байланысты оң жақ немесе сол жақ бұруды орындау қажет.