- •1. Ақпараттық іздеудің қарапайым есебі
- •3.Бинарлы ағашты симметриялы ретпен айналу.
- •4.Бинарлы ағашты тура ретпен айналу.
- •5.Бинарлы ағашты кері ретпен айналу.
- •6.Avl ағашта сол жақ және оң жақ бұрылыс операциялары.
- •7. Ықтималды іздеу ағашы.
- •8.Бинарлы іздеу ағашының элементтерін жою.
- •9.Қызыл-қара ағаш және оның ерекшеліктері.
- •Қызыл-қара ағаштың биіктігі
- •Операциялар.
- •Қызыл-қара ағаштың артықшылығы..
- •10.Бинарлы ағаш тұрғызу алгоритмі және олардың арнайы ерекшеліктері.
- •11.Толықтау бинарлы ағаш.
- •12.Бинарлы ағаштың көрсетілуі.
- •13.Іздеу бинарлы ағашынан элементті жою
- •14.O(n log2n) күрделілігімен сұрыптау.
- •15.O(n2) күрделілігімен сұрыптау.
- •16.Бинарлы ағаштармен жасалатын стандарты операциялар.
- •17.Бинарлы ағаштар және оның қолдануы.
- •18.Бинарлы ағашта кесте құру және оның ерекшеліктері.
- •20.Шелл сұрыптауы (Shell_sort) және оның ерекшеліктері.
- •21.Quick_sort сұрыптауы оның ерекшеліктері.
- •22.Пирамидалы сұрыптау алгоритмі (Heap_sort) ж/е оның ерекшелік/і.
- •23.Newman_sort және оның ерекшеліктері.
- •24.Экстремальды қасиет/і бар бинарлы ағаштың арнайы ішкі класс/ы.
- •25.Бинарлы ағаштар қолданыстары және жалпылаулары.
- •26.Квадраттық xештеу.
- •27.Avl ағаштары.
- •28.Стек
- •29.Сызықты хештеу.
- •30.Қос хештеу.
30.Қос хештеу.
Қос хештеу тәсілінде дәстүрлі екі хеш-функция қолданылады: оның біріншісі хеш-кестесінің жолының нөмірін алғашқы әрекетте анықтауда қолданылатын h(p) хеш-функциясы; екіншісі h0(p) хеш-функциясы коллизия жағдайында сынақтарды реттеуде қолданылады, сондықтан:
{ xmodm |x=(h(p) + i*h0(p)), i=0,1,2,…,m-1}, (**)
Әр түрлі і үшін жасалған есептеулерден мына сынақтар тізбегін аламыз:
h(p), (h(p) + h0(p)) modm, (h(p) + 2 h0(p)) modm, ..., (h(p) + (m-1) h0(p)) modm, …
Бұдан жаңа хеш-функция жазбасындағы екінші қосылғыштың тек қана сынақ нөміріне ғана емес сонымен қатар, оның кілтіне де тәуелді екенін көруге болады. Және де бұл жағдай әр түрлі екі кілттер үшін сынақтар тізбегі ерекшеленетінінне негіз болады деуге болады. h0 функциясының қолайлы таңдалынуы оның сапасын қаматамасыз етеді, және мұндағы m жай сан болуы тиіс. Қос хештеудің хеш-функциясын анықтауына сүйеніп, егер кейбір p2 кілт үшін кез-келген h(p)+і* h0(p) кездейсоқ бірінші есептелген мән болса, онда келесісі h(p) + (і+1)* h0(p) болмай, h(p)+і* h0(p)+ h0(p2) болады.
Қос хештеу есептеудің күрделенуіне әкеледі, екінші жағынан колизияларды шешуде қолайлы тәсіл береді. Осыдан h0(p) функциясы күрделі есептелуі тиіс емес.
Жаттығу: (**) формуласы бойынша қос хештеуде h0 және m өзара жай сан болса, р кілті үшін (**) формуласымен анықталатын сынақтардың тізбегі хеш-кестесінің жолдарының {0,1,2,…,m-1} жиынын толық жабатынын дәлелдеу қажет.
h0(p) функциясы үшін [25] көрсетілгендей h0(p,і)=i*h(p)+1 деп алуға болады және де, егер h(p)=k деп белгілесек, онда ол келесі сынақтар тізбегін береді:
k, 2k+1, 5k+2, 10k+3, …, k+i*(i*k+1), …
Егер қандай да бір р кілті үшін алғашқы мәні р кілтінің бір сынақ мәнімен кездейсоқ бірдей болғаны анықталса, мысалы 2k+1, онда р кілтінің сынақтар тізбегі р кілтіне қарағанда өзгеше болады, дәлдеп айтсақ 2k+1, 4k+3, 10k+7, …, мұндағы соңғы есептеудің мәні келесі алғашқы формула негізінде алынған:
((h(p)+2h0(p))modm=(h(p)+2h0(p,2))modm=(10k+7)modm
Ендігі кезекте хеш-функциясын таңдауымыз қақтығысқа әкелмейді деп үміттеніміз. Алайда 2h0(p,і)=i*h(p)+1 түрінде таңдалған хеш-функциялы (**) хештеу схемасын қолдану мәндерінің жан-жақтылығына қарамастан біршама шектелген.
Жаттығу: р үшін сынақтың бірінші есептелген мәні 4k+3-ке тең болған жағдайда сынақ тізбегінің алғашқы 4 мәнін есептеу к/к.
Тапсырма: h0(p,і)=i*h(p)+1, і=1,2,…,m-1 қосалқы хеш-функциясы бар қос хештеу схемасындағы хеш-кестесіне элементті енгізу мүмкіндігін зерттеу керек.
Алайда h0(p) функциясын таңдаудың оданда қызықты нұсқалары бар, мысалы:
h0(p)=q-(pmodq)
мұндағы q-m-нен кем жай сан, яғни q<m. Мысалы m=10, q=7 жағдайын қарастырайық, және мұндағы массив 119, 78, 49, 59, 11, 31, 29, 103, 39:
-
0
1000
1000
1
11
11
11
11
11
2
39
3
59
59
59
59
59
59
4
5
|
31
31
31
31
6
49
49
49
49
49
49
49
7
29
29
29
8
78
78
78
78
78
78
78
78
9
119
119
119
119
119
119
119
119
119
көріп тұрғанымыздай 9-шы қадамнан кейін бір ғана бос тор көз қалды, белгінің 28-ге тең мәні үшін элементті бұл бос ұяшыққа қоя аламыз ба, соны көрейік. Бұл жағдайға дейін процесс барысында пайда болған барлық коллизияларды сәтті шештік. Сөйтіп, h(28,0)=8, мәні 78 болатын колллизияны береді, ары қарай
h(28,1)=5,
h(28,2)=2,
h(28,3)=9,
h(28,4)=6,
h(28,5)=3,
h(28,6)=0,
h(28,7)=7,
h(28,8)=4,
Бұл жағдайда да кірістірумен іздеу қосымша 8 сынақ орындағанымызға қарамастан сәтті өтті деуге болады.
Қос хештеуді қорыта келе, бұл тәсілде хештеу функциясын күрделендіру арқылы екінші кластерлердің проблемаларын болдырмауға әкелетінін көруге болады. Қос хештеу процедурасының қолайлылығы бағалаулармен де нақтыланады.
1/а * ln(1/(1-a)) бағасы хеш-кестеде бар элементтерді іздеу сынақтарының ортаңғы санын береді.
1/(1-а) бағасы хеш-кестесіне жаңа элементті қойғандағы сынақтардың ортаңғы санын береді. Бұл баға хеш-кестеде элемент жоқ жағдайда да іздеуде сақталынып қалады. Бұл бағаларды сызықтық хештеу мен төртбұрыштық хештеу бағаларымен салыстыру да қызығушылық туғызады.
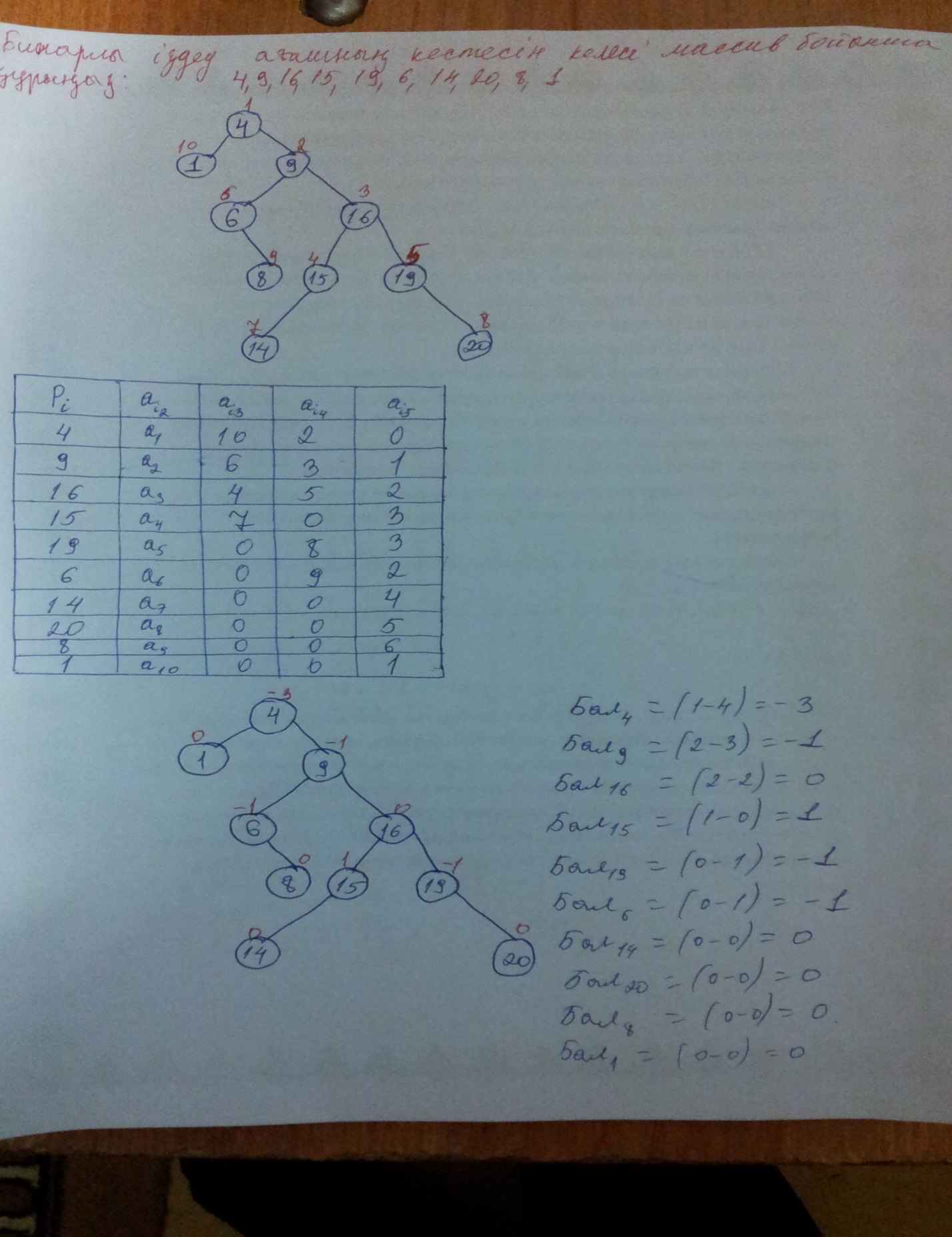
Бинарлы іздеу ағашның кестесін келесі массив бойынша құрыңыз: 4,9,16,15,19,6,14,20,8,1
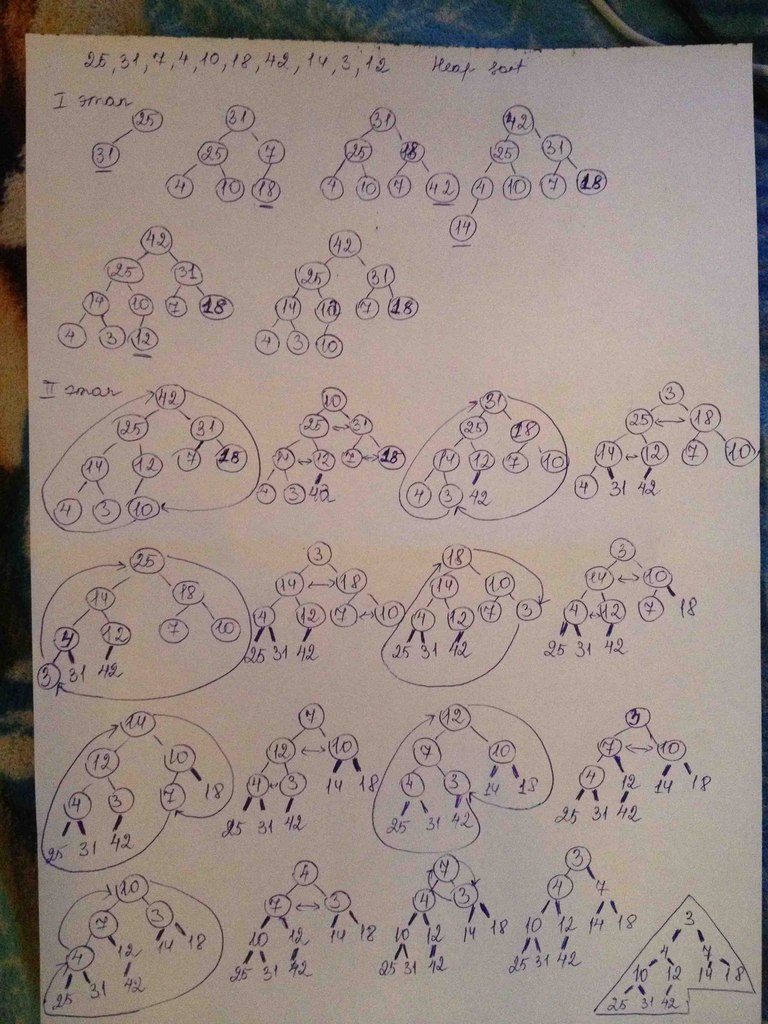
Бинарлы іздеу ағашның кестесін келесі массив бойынша құрыңыз: 25,31,7,4,10,18,42,14,3,12
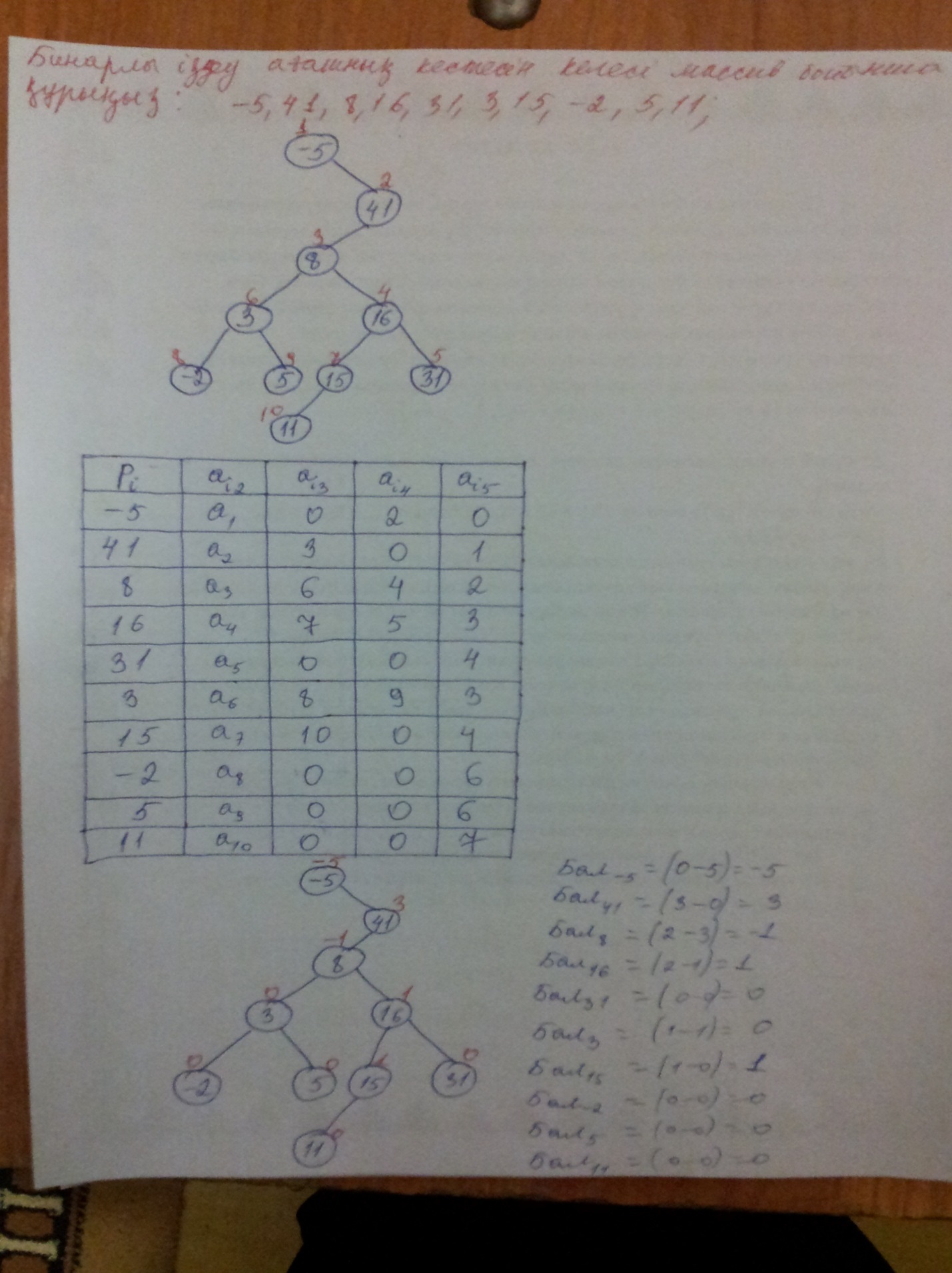
Бинарлы іздеу ағашның кестесін келесі массив бойынша құрыңыз: -5,41,8,16,31,3,15,-2,5,11
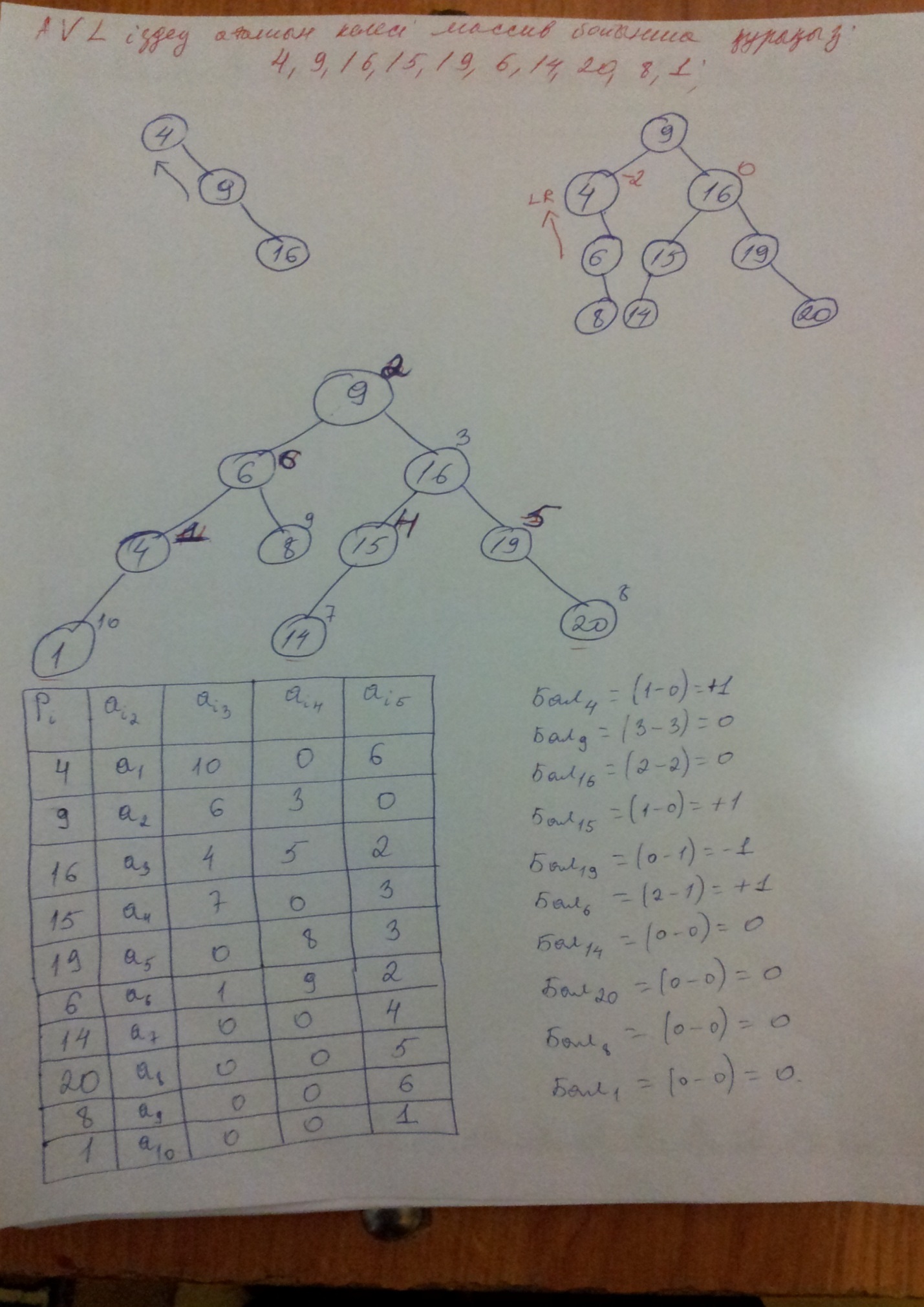
AVL іздеу ағашын келесі массив бойынша құрыңыз: 4,9,16,15,19,6,14,20,8,1
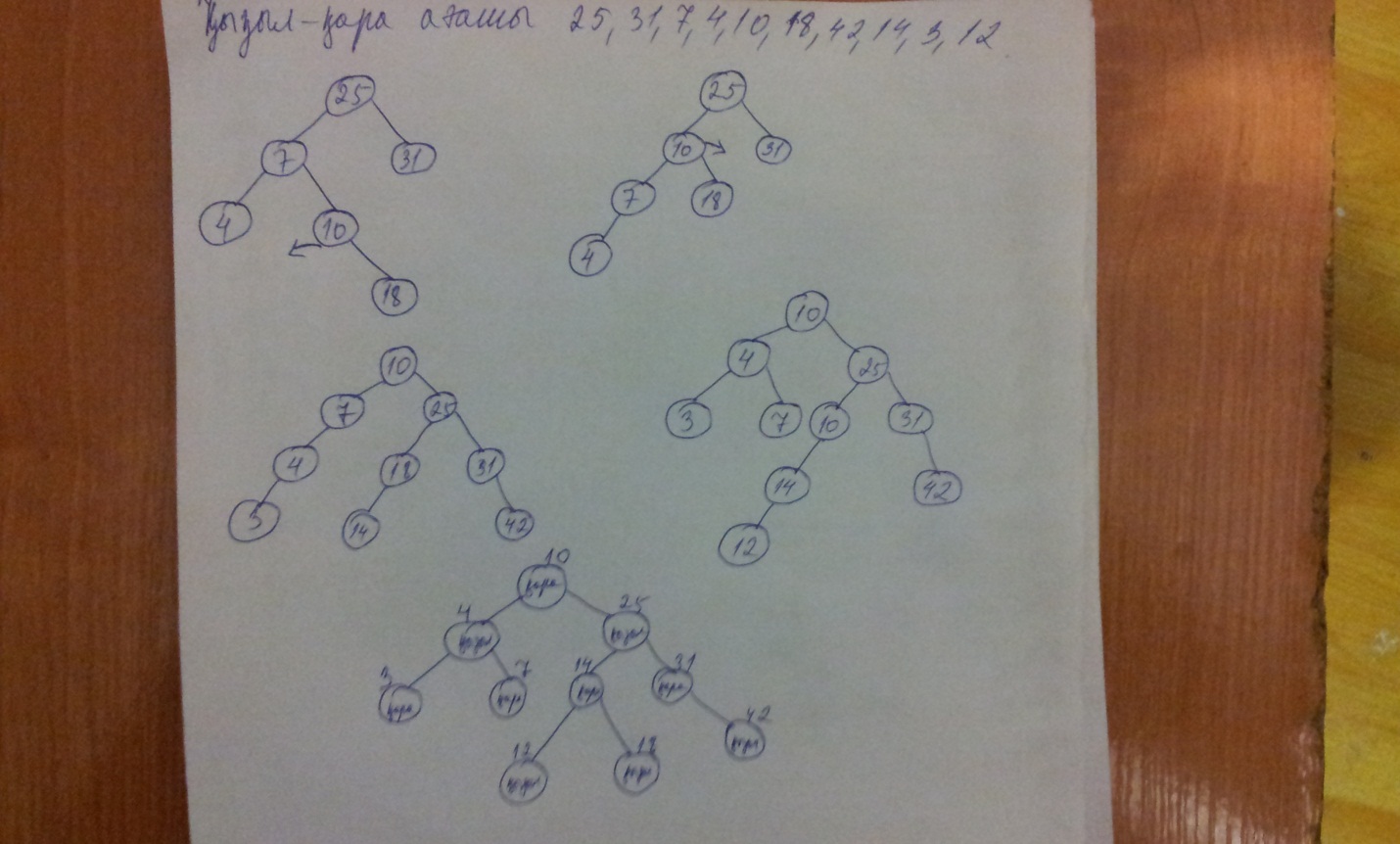
AVL іздеу ағашын келесі массив бойынша құрыңыз: 25,31,7,4,10,18,42,14,3,12
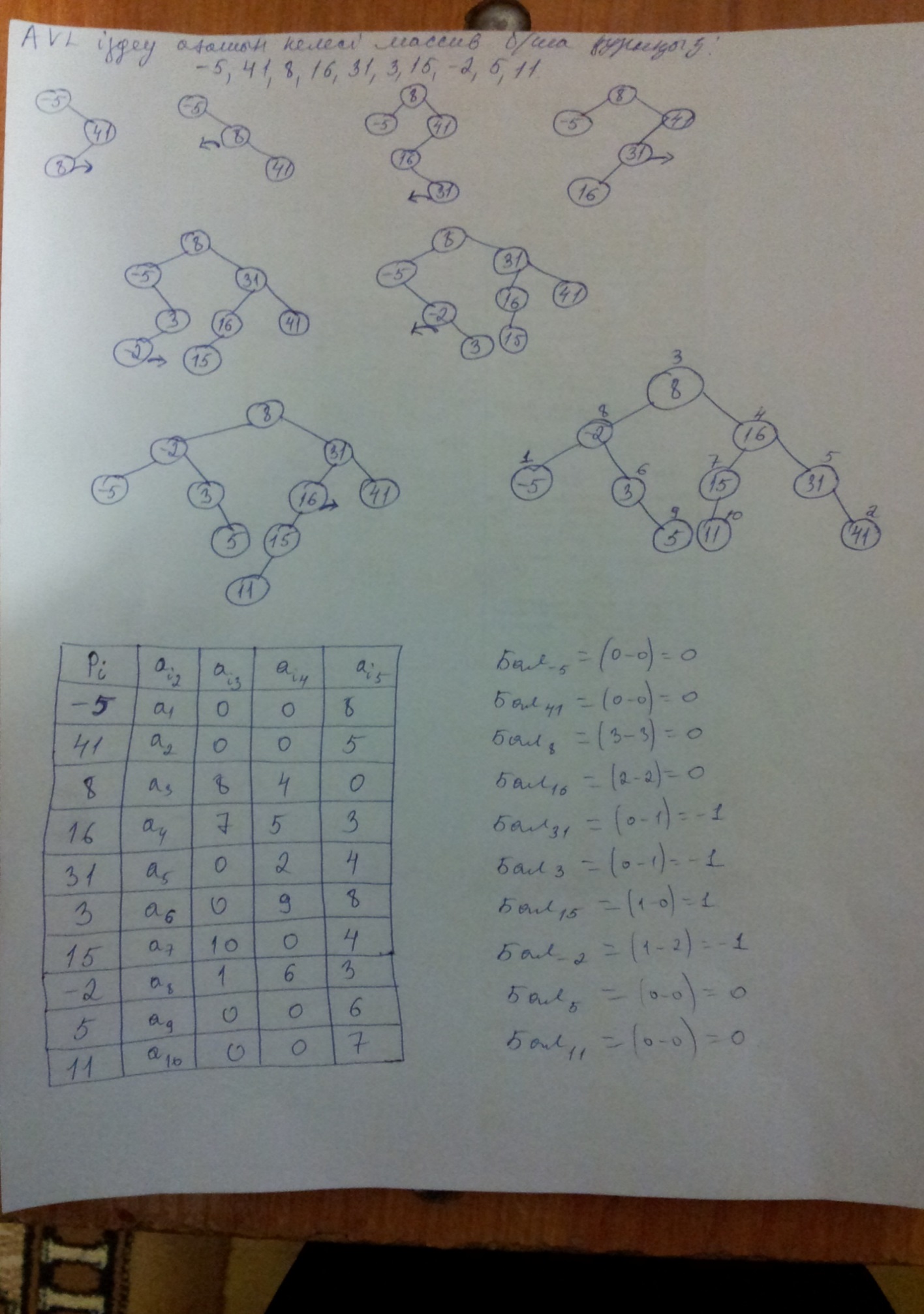
AVL іздеу ағашын келесі массив бойынша құрыңыз: -5,41,8,16,31,3,15,-2,5,11
Келесі массивке кызыл-қара ағаш құрыңыз: 4,9,16,15,19,6,14,20,8,1
Келесі массивке кызыл-қара ағаш құрыңыз: 25,31,7,4,10,18,42,14,3,12
Келесі массивке кызыл-қара ағаш құрыңыз: -5,41,8,16,31,3,15,-2,5,11
Келесі массивке Quick_sort сұрыптау әдісін қолданыңыз: 4,9,16,15,19,6,14,20,8,1
Келесі массивке Quick_sort сұрыптау әдісін қолданыңыз:25,31,7,4,10,18,42,14,3,12
Келесі массивке Quick_sort сұрыптау әдісін қолданыңыз: -5,41,8,16,31,3,15,-2,5,11
Келесі массивке Шелл сұрыптау (Shell_sort) әдісін қолданыңыз: 4,9,16,15,19,6,14,20,8,1
Келесі массивке Шелл сұрыптау (Shell_sort) әдісін қолданыңыз: 25,31,7,4,10,18,42,14,3,12
Келесі массивке Шелл сұрыптау (Shell_sort) әдісін қолданыңыз: -5,41,8,16,31,3,15,-2,5,11
Келесі массивке пирамидалы сұрыптау алгоритмін (Heap_sort) қолданыңыз: 4,9,16,15,19,6,14,20,8,1
Келесі массивке пирамидалы сұрыптау алгоритмін (Heap_sort) қолданыңыз: 25,31,7,4,10,18,42,14,3,12
Келесі массивке пирамидалы сұрыптау алгоритмін (Heap_sort) қолданыңыз: -5,41,8,16,31,3,15,-2,5,11
Келесі массивке көпіршікті сұрыптау (Bubble_sort) әдісін қолданыңыз: 4,9,16,15,19,6,14,20,8,1
Келесі массивке көпіршікті сұрыптау (Bubble_sort) әдісін қолданыңыз: 25,31,7,4,10,18,42,14,3,12
Келесі массивке көпіршікті сұрыптау (Bubble_sort) әдісін қолданыңыз: -5,41,8,16,31,3,15,-2,5,11
Келесі массивке Newman_sort сұрыптау әдісін қолданыңыз: 4,9,16,15,19,6,14,20,8,1
Келесі массивке Newman_sort сұрыптау әдісін қолданыңыз: 25,31,7,4,10,18,42,14,3,12
Келесі массивке Newman_sort сұрыптау әдісін қолданыңыз: -5,41,8,16,31,3,15,-2,5,11
AVL ағашта сол жақ және оң жақ бұрылыс операция/ы. 6
AVL ағаштары. 27
AVL-ағаштар және толыққа жуық бинарлы ағаштар. 2
Newman_sort және оның ерекшеліктері. 23
O(n log2n) күрделілігімен сұрыптау. 14
O(n2) күрделілігімен сұрыптау. 15
Quick_sort сұрыптауы оның ерекшеліктері. 21
Ақпараттық іздеудің қарапайым есебі 1
Бинарлы ағаш тұрғызу алгоритмі ж/е о/ң арнайы ерекш./і. 10
Бинарлы ағашта кесте құру және оның ерекшеліктері. 18
Бинарлы ағаштар және оның қолдануы. 17
Бинарлы ағаштар қолданыстары және жалпылаулары. 25
Бинарлы ағаштармен жасалатын стандарты операция/. 16
Бинарлы ағашты кері ретпен айналу. 5
Бинарлы ағашты симметриялы ретпен айналу. 3
Бинарлы ағашты тура ретпен айналу. 4
Бинарлы ағаштың көрсетілуі. 12
Бинарлы іздеу ағашының элементтерін жою. 8
Квадраттық xештеу. 26
Көпіршікті сұрыптауы (Bubble_sort) ж/е оның ерекшелік/і. 19
Қос хештеу. 30
Қызыл-қара ағаш және оның ерекшеліктері. 9
Пирамидалы сұрыптау алгоритмі ж/е оның ерекшелік/і. 22
Стек. 28
Сызықты хештеу. 29
Толықтау бинарлы ағаш. 11
Шелл сұрыптауы (Shell_sort) ж/е оның ерекшеліктері. 20
Ықтималды іздеу ағашы. 7
Іздеу бинарлы ағашынан элементті жою. 13
Экстремальды қасиеттері бар бинарлы ағаштың арнайы ішкі класы. 24
6.
5.

4.
11.

10.

12.
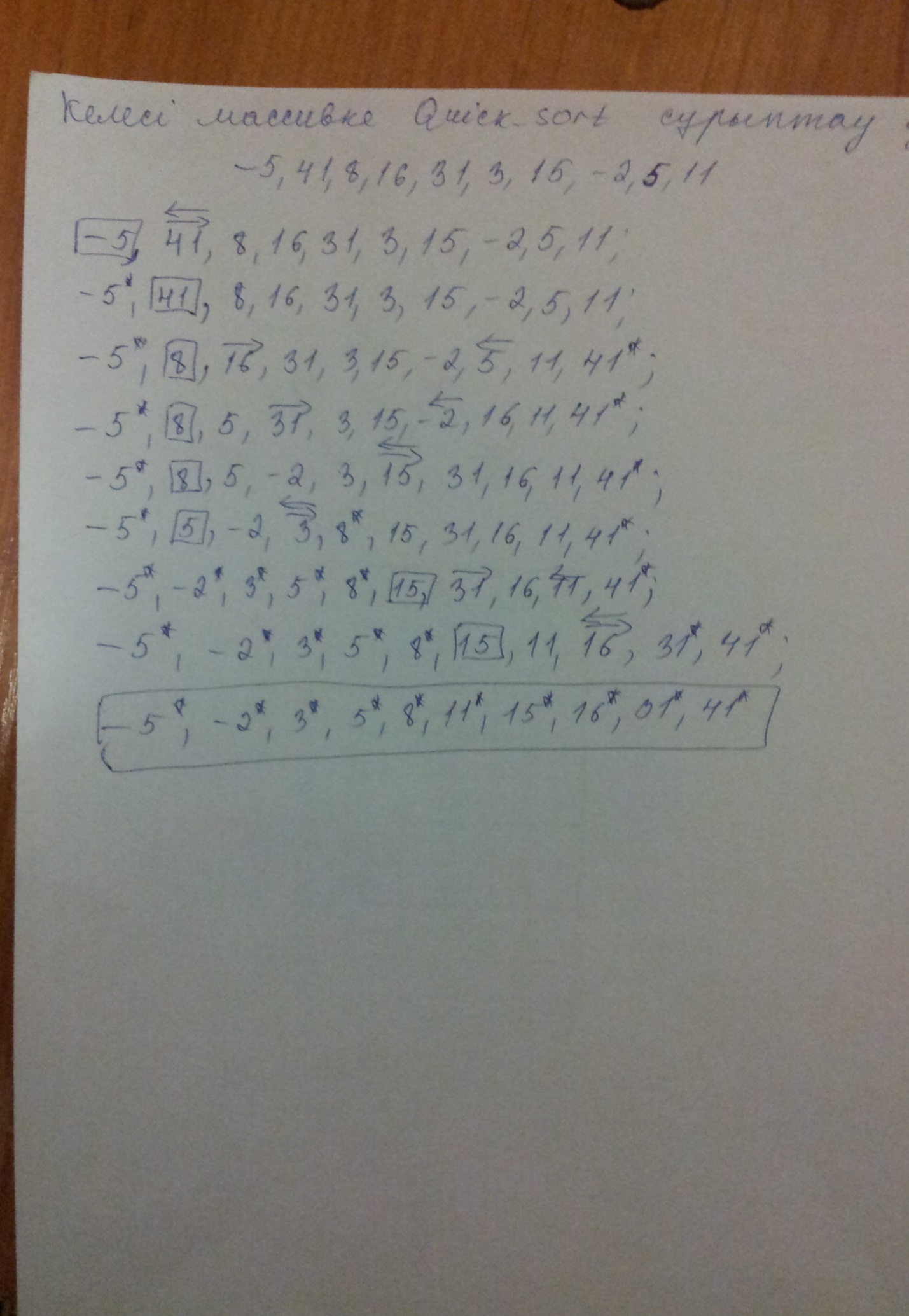
3.
2.

1.
14.

15.

13.

7.

8.
9.

24Newman-20Bubble sort.

22-23.

21-19.

18. -5,41,8,16,31,3,15,-2,5,11

16. 4,9,16,15,19,6,14,20,8,1
17.