22.Пирамидалы сұрыптау алгоритмі (Heap_sort) ж/е оның ерекшелік/і.

Қарастырылатын алгоритм таңдаумен (элементті) сұрыптау алгоритм/і классына жатады.Бірақ бұл алгоритмнің өзінің ерекше қасиет/і бар. Біріншіден, бастапқы массив бинарлы ағашпен беріледі. Бұл бинарлы ағаш құрылысы жағынан ерекшеленіп келеді, ондай ағаштарды толықтау ағаштар деп атайды.

3.1. а) сурет 3.1. б) сурет

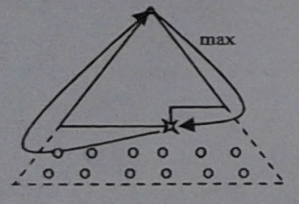
Реттеу процессі екі этаптан тұрады.Бірінші этапта пирпмида тәріздес ағаш түзіледі.Бұл этаптың кез-келген қадамында ағаш 3.1 а және 3.2 б сурет/інде көрсетілгендей. 1-этаптың нәтижесі келесі қасиет/ге ие пирамида болады: ағаш түбірінен қорытынды төбеге шығатын кез-келген жолында түйіндер кемімелі, дәлелдеп айтқанда өспелі емес ретпен орналасады; пирамида ағаштың жоғарыдан төменге, сол жақтан оңға қарай түзіледі. 2-этапта құрылған ағаш-пирамидасында түйінд/іне бекітілген

Массив элементтеріне түпкілікті реттеуге пайдаланылады. Бұл этапта пирамиданың элементтерін реттеу бағыты пирамиданың оң жағынан солға қарай, төменнен жоғарыға қарай қажет болған жағдайда алмастырылады. Екінші этап бірінші фазадан тұрады. Бірінші фазада массивтің реттелмеген бөлігіндегі ағымдық максималды элемент (бұл фазада оның пирамиданың төбесінде орналасқанын ұмытпау керек) пирамиданың төменгі оң бұрышында орналасқан элементпен алмастырылады. Сөйтіп ағымдық максималды элемент реттелген массивте өзінің орнын табады. Осыдан кейін бұл максималды элемент те, оның орны да реттеуге қарастырылмайды. 2-этаптың 1-фазасының нәтижесінде пирамиданың төбесінде, яғни ағаштың түбірінде, оның құрылысының бұзылуына кездесеміз. Сондықтан 2-фазада өзгенген пирамиданың құрылысы қайтадан құралады.

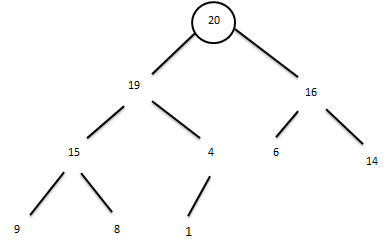
Пирамидалы сұрыптау алгоритмін мысалмен қарастырайық: 4,9,16,15,19,6,14,20,8,1 массиві берілсін.

Бірінші этапта алғашқы пирамиданы құрудан басталады. Мұнда 4,9,16 мәнді төбелерді тізбектеп енгіземіз.

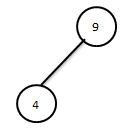
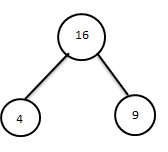
келесі 15,19

одан кейін 6,14

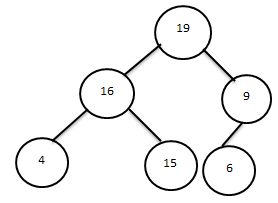
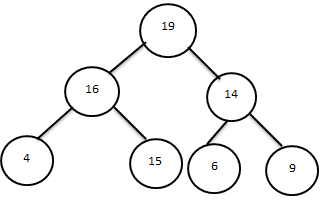
әрі қарай 20,8 элементтерді

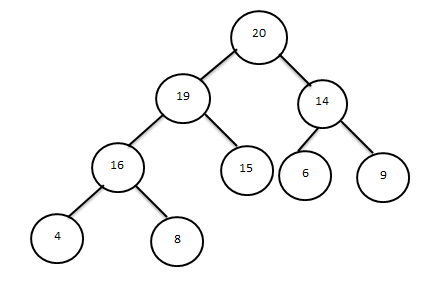
Соңында массивтің соңғы элементі пирамиданың түбірінде өзінің орнын табады

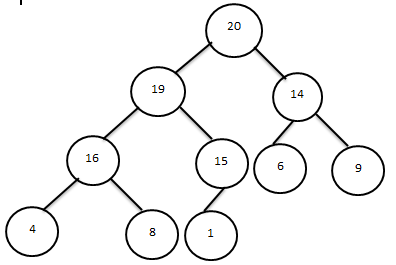
Екінші этапта пирамиданың төбесі мен бұрыштық түйін ауыстырылады.

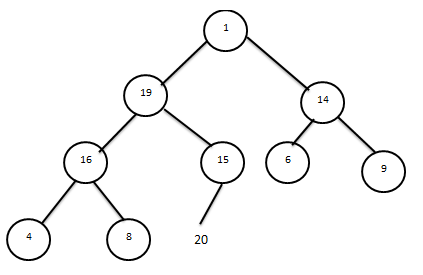
мәні 20 элемент өзінің болашақ сұрыпталған массивте соңғы орынын табады. Келесі қадамда алгоритм пирамиданың өзгертілген құрылысын қалпына келтіреді. Ол үшін мәні 1-ге тең массив элементін пирамида деңгейлері мен тармақтары арқылы жүргізіп орынын анықтау қажет. Бұл процесс пирамиданы қалпына келтіреді.

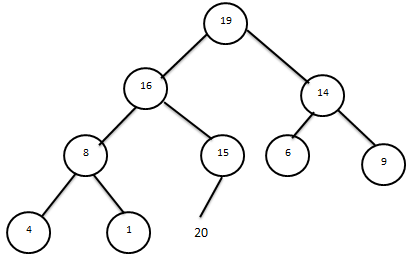
Тағыда алмастыру жүргіземіз

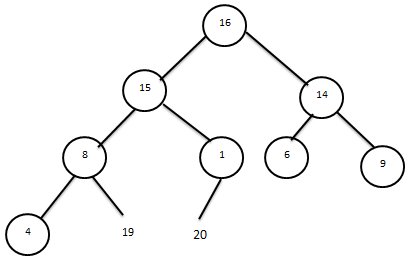
пирамида құрылысы өзгертеді.Келесі қадамда мәні 4-ке тең элементтің орнын тауып,пирамиданы қалпына келтіреміз.

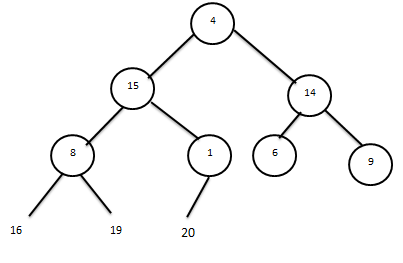
т.с.с

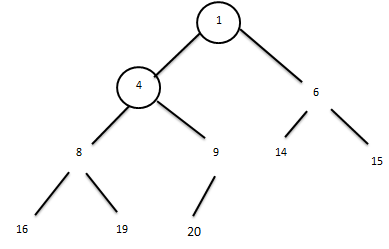
Соңғы қадамда қалыптасқан пирамиданы аламыз.

осы жерде жалпы айтқанда бірінші этап «алғашқы мссив төмендегідей құрылысты ағаш түрінде берілуі мүмкін» деген болжаумен бастауға болатынын байқауға болады:

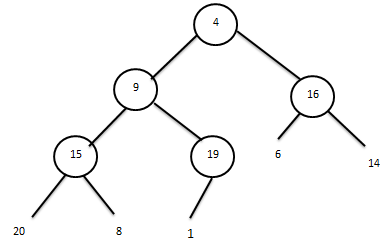
3.2.а сурет

Бұл мысалда алмастыруларды нөмері n/2 пирамида түйінен бастау қажет болады.Сурет 3.2.а түйін мәні 19-ға тең:

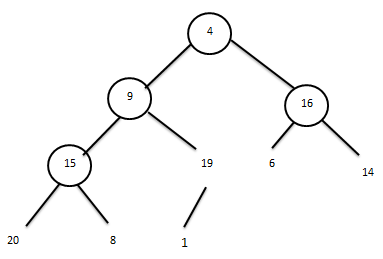
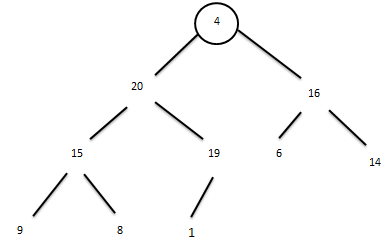
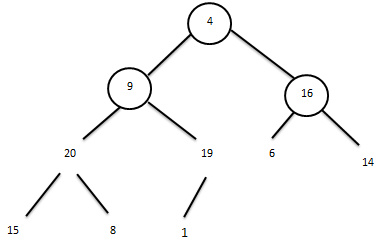
Алмастырулар бізді таныс пирамида типіне әкеледі: