Математическая модель случайной погрешности

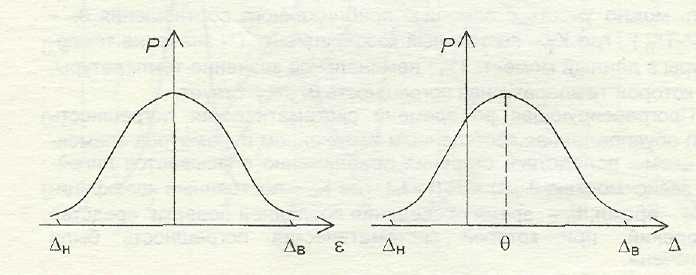
Быстрые флуктуации ε (t) определяют случайную погрешность, ко­торую приближенно описывают эргодическим случайным процессом с нулевым математическим ожиданием. При проведении измерений с многократными наблюдениями эта составляющая проявляется в виде случайной величины, принимающей значения εi= ε (t i), взятые в моменты t i (i = 1,2,...,п) проведения наблюдений. Наиболее полной характеристикой случайной погрешности являют­ся функции распределения. По известной дифференциальной функции распределения (плотности вероятности) ρ(ε) можно опре­делить вероятность пребывания случайной погрешности в заданных

границах от ∆_н до ∆_в:

Так как ε = х - X , где X - истинное, ах- измеренное значение изме­ряемой величины, то Р∆ = Р{х - ∆_вн < X < х + ∆_вн} (∆_вн — симметрич­ные границы интервала). Следовательно, вероятность Р∆ соответ­ствует вероятности пребывания истинного значения на интервале от х - ∆_вн до х + ∆_вн. Поскольку общая погрешность ∆ = Θ + ε, то ее плотность вероятности можно определить, сместив график ρ(ε) на Θ. В данном случае нижнюю ∆_н и верхнюю ∆_в границы интервала, в котором с вероятностью Р∆ лежит погрешность, выбирают симмет­рично относительно математического ожидания, поэтому I∆_НI≠ ∆_е

4.10.4. Примеры законов распределения погрешностей

Для анализа результата измерений необходимо знать законы рас­пределения отдельных составляющих погрешности, по которым можно определить закон распределения общей погрешности и ре­шить вопрос о вычислении границ погрешностей. В некоторых слу­чаях удается оценить законы распределения составляющих по­грешности до проведения опыта на основе анализа причин их воз­никновения.

Равномерный закон. Этому закону подчи­нены погрешности, возникающие при кван­товании и дискретизации сигнала. Напри­мер, при измерении постоянного напряже­ния U_x путем его сравнения с образцовым напряжением, изменяющимся по ступенча­тому закону с постоянным шагом Uст, ре­зультат измерений определяется числом n ступенек, зафиксированным с помощью электронного счетчика, и погрешностью квантования ∆U_кв: U_x = nUст - ∆U_KB. Поскольку значение измеряемого напряжения неизвестно и нельзя указать область его предпочтительных значений, погрешность кван­тования считают распределенной по равномерному закону от 0 до Uст. Систематическая погрешность

График плотности вероятности случайной погрешности ε = ∆U_кв – Θ получается смещением графика ρ(U_KB ) на Uct/2. Предельная по­грешность ∆п = Uct /2. СКО случайной погрешности

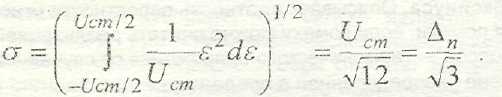
Для погрешностей, о которых ничего не известно, кроме их преде­лов, равномерный закон является удобной математической моде­лью, как дающий наибольшую погрешность измерений. Например, при анализе неисключенной систематической погрешности удается оценить лишь ее предельные значения ±Θ_н. Закон распределения неисключенной систематической погрешности моделируют равно­мерным законом с СКО σ = Θ/√12. Согласно ГОСТ 8.009—84 равно­мерно распределенной считают погрешность из-за вариации пока­заний в пределах +Н/2 с СКО σ =H√ 12 , где Н =IС_б —С_мI.

Например, при измерении временного интервала цифровым мето­дом, если начало измеряемого интервала не синхронизировано с последовательностью счетных импульсов, результат измерений T_x=nT₀-∆t_H+∆t_k =nT₀-∆t_д, где ∆t_н и ∆t_K погрешности дискретизации в начале и конце интервала Т_х, ∆t_д общая погрешность дискретиза­ции. Погрешности ∆t_н и ∆t_K подчинены равномерному закону с пре­дельными значениями 0 и Т₀. Если интервал Т_х не измерен, то случайные погрешности независимы, а закон распределения общей погрешности дискретизации ∆t_д треугольный с предельными значе­ниями ±Т₀ .

Характеристики окружающей среды, в которой проводятся измере­ния, называют условиями измерений. Это климатические условия (температура, относительная влажность воздуха, атмосферное давление), электрические и магнитные поля, механические и аку­стические факторы (вибрации, ударные нагрузки, сотрясения), ио­низирующие излучения, газовый состав атмосферы и т.п. Так как они оказывают влияние на результат измерений, то для средств измерения в нормативно-технической документации всегда указы­ваются условия, в которых нормированы их метрологические ха­рактеристики.

Метрологические характеристики средств измерений нормируют раздельно для нормальных и рабочих условий применения.

4.12. Организация измерительного эксперимента

Измерение выполняется оптимально, если результат и желаемая точность достигнуты самыми простыми средствами и в соответст­вии с простейшей стратегией.

Этап 1

Подготовка включает уточнение задачи измерений, планирование измерительного эксперимента, выбор требуемых методов и техни­ческих средств, в том числе и вспомогательное оборудование (ис­точники питания, соединение с измеряемой средой, средства со­пряжения, средства подвода охладителя, если требуется и т.д.); калибровку механических и юстировку оптических приборов, гра­дуировку электронных средств.

Планирование измерительного эксперимента

Эксперимент - это метод познания, при помощи которого в кон­тролируемых и (или) управляемых условиях исследуются явления действительности. Целью эксперимента может быть установление наличия/отсутствия предполагаемого теорией явления (качествен­ный эксперимент); проверка гипотез и предсказаний теории (ре­шающий эксперимент); проверка конкретных теоретических моде­лей путем мысленных процедур над идеальными объектами (мыс­ленный эксперимент); исследование материальных моделей (мо­дельный эксперимент) и др.

Измерительный эксперимент позволяет выявить количественную определенность какого-либо свойства объекта. При этом объект представляют в виде «черного ящика», т. е. системы, структура ко­торой скрыта от наблюдателя, а суждение о ее функционировании создается только на основании анализа внешних воздействий (управляющих и возмущающих) и соответствующих им реакций сис­темы (параметров состояния).

Управляющие (входные) параметры Xi (i=1, 2, ..., к) представ­ляют собой независимые переменные, которые можно изменять с целью управления выходными параметрами объекта. Они могут быть измерены и называются также факторами. Каждый фактор имеет область определения, которая должна быть установлена до проведения эксперимента.

Возмущающие воздействия Vn (n=1,2, .... р) в общем случае не поддаются контролю и проявляют себя как случайные величины или функции времени. Наличие возмущающих воздействий приводит к тому, что зависимость выходных параметров объекта от входных становится неоднозначной.

К параметрам состояния (выходные параметры) Yj (j=1, 2,..., r) относится совокупность контролируемых или вычисляемых пара­метров, характеризующих состояние объекта. В простейшей ситуа­ции экспериментатора интересует поведение одного выходного па­раметра, характеризующего объект. Чаще всего это критерий опти­мальности (целевая функция), зависящий от входных параметров.

Планирование позволяет повысить эффективность эксперимен­тальных исследований. Цель его - выбрать из множества воз­можных планов проведения эксперимента одного в некотором смысле наилучшего, согласно критерию сравнения или целевой функции. Критерием может быть точность, продолжительность, стоимость эксперимента и т.п.

При пассивном эксперименте (наблюдении) информацию полу­чают в условиях нормального функционирования объекта исследо­вания. Т.к. исследователь не имеет возможности воздействовать на изучаемый объект, то задача планирования эксперимента сводится к оптимальной организации пассивного сбора информации и вклю­чает в себя такие вопросы, как выбор интервалов времени между моментами измерения, задание числа выполняемых измерений, выбор метода обработки экспериментальных данных и т. п.

При активном эксперименте осуществляется искусственное воз­действие на объект по заранее спланированной программе. Он по­зволяет быстро вскрывать закономерности, находить оптимальные режимы функционирования объекта, но его труднее осуществить: вмешательство в технологический процесс может привести к сни­жению производительности, выпуску бракованной продукции. В не­которых случаях (например, при астрономическом наблюдении) ак­тивный эксперимент невозможен.

Пример выбора способа решения поставленной задачи

Задача. Определить с помощью некоторого массоизмерительного устройства массу трех объектов (А, В и С).

Решение. Обозначим: у_i- результат взвешивания; гп_к - масса ука-занного объекта; σ_j² - дисперсия указанного результата; 2σ² [у] -дисперсия результата каждого единичного измерения.

Вывод: Так как в обоих случаях проведено одинаковое количество опытов, а второй способ исключает влияние смещения нуля массо-измерительной системы и дает в два раза меньшую дисперсию ре­зультатов измерения, то можно утверждать, что второй план экспе­римента лучше первого.

Этап 2

На втором этапе осуществляется передача измеряемой величины к средству измерения, управление средством измерения и контроль его функций, отслеживание параметров внешних влияющих вели­чин (температуры, влажности и др.) и поддержка их постоянства; восприятие измеренных значений.

При этом решаются следующие вопросы. Задан ли путь решения или требуется его выбор? Запрашивается только определенное средство измерения или требуется его выбор? Имеется ли выбран­ное средство измерения в наличии или нужно его приобрести? Под­готовлено ли оно к работе? Достаточно ли одного измерения или его надо повторить?

Этап 3

Оценивание результата измерений: все виды вычислений, в том числе внесение корректив в измеренные значения, определение результата косвенных измерений, определение среднего значения, определение погрешности измерений.

При этом выясняется, достаточно ли полученной информации или требуются дополнительные исследования?

4.12.2. Стратегии измерений

Каждая измерительная процедура нуждается в разработке соответ­ствующей стратегии. Такой организационный подход создает благо­приятные предпосылки для решения измерительных задач, в том числе с точки зрения удовлетворения технических и экономических условий.

Вспомогательным средством планирования (поиска оптимального решения) являются блок-схемы (диаграммы) планирования.

Не всегда возможно измерить желаемую физическую величину не­посредственно, например, в том случае, когда интересующая нас величина флуктуирует быстрее, нежели может отслеживать измери­тельная система (частотный спектр измеряемого сигнала в этом случае шире полосы пропускания измерительной системы). А если полоса пропускания измерительной системы значительно превосхо­дит ширину спектра сигнала, то измерительная система использует­ся не оптимально.

4.13. Процесс измерения

4.13.1. Однократное измерение

Подавляющее большинство измерений являются однократными. В обычных условиях их точность вполне приемлема, а простота, вы­сокая производительность (количество измерений в единицу вре­мени) и низкая стоимость (по оценке трудозатрат) ставят их вне конкуренции. В результате из множества возможных значений от­счета получается и используется только одно, а представление о законе распределения вероятности отсчета и его среднеквадратическом отклонении формируется исключительно на основе априор­ной информации.

4.13.2. Многократное измерение

Многократное измерение одной и той же величины постоянного размера производится при повышенных требованиях к точности из­мерений. Это сложные, трудоемкие и дорогостоящие измерения, целесообразность которых должна быть всегда обоснована. Они характерны для профессиональной метрологической деятельности и выполняются в основном сотрудниками государственных и ведом­ственных метрологических служб, а также при тонких научных экс­периментах.

Обработка результатов нескольких серий измерений

Иногда многократное измерение одной и той же величины постоянного размера производится в несколько этапов, разными людьми, в различ­ных условиях, в разных местах и в разное время. Результат такого из­мерения определяется несколькими сериями полученных значений, которые в силу различных обстоятельств могут отличаться по своим статическим характеристикам. Серии называются однородными, если состоят из значений, подчиняющихся одному и тому же закону распре­деления вероятности и неоднородными в противном случае. Проверка однородности является обязательной при выборе способа совместной обработки результатов нескольких серий измерений и строится на сравнении эмпирически полученных значений средних арифметических результатов измерений и их дисперсий в каждой серии.

Исключение ошибок

Надежность эргономической системы, в которую входит человек, окру­жающая среда, объект измерений и средства измерений, не безгранич­на. В ней могут происходить сбои: отказы аппаратуры, скачки напряже­ния в сети питания, сейсмические сотрясения, отвлечение внимания оператора, описки в записях и многое другое, не имеющее отношения к измерениям. Вероятность появления ошибки в такой системе, исходя из теории больших систем, не так уж и мала.

При однократном измерении ошибка может быть обнаружена толь­ко путем логического анализа или сопоставления результата с ап­риорным представлением о нем.

При многократном измерении одной и той же величины посто­янного размера ошибки проявляются в том, что результаты отдель­ных измерений заметно отличаются от остальных. Если это отличие настолько велико, что ошибка очевидна (грубые промахи), то выяс­няют и устраняют причину ее появления или отбрасывают этот ре­зультат, как заведомо неверный. Незначительное отличие может быть следствием, как ошибки, так и рассеяния результата. К этому случаю применимо правило:

σ определяет границы некоторого интервала, называемого доверительным, в пределах которого располагается измеряемое значение.

4.14. Результат измерений

Результат измерения по шкале порядка представляет собой ре­шение опытным путем неравенства Qi>, = или <Qj с указанием его вероятности.

Результат измерения по градуированным шкалам - числовое зна­чение с внесенной в него поправкой и в определенных единицах измерения с указанием его вероятности.

Формы выдачи и представления результата измерений

Аналитическая. При отображении единственного результата кор­ректной является запись в форме уравнения, в котором слева за­писана измеряемая величина (в виде символьного обозначения ли­бо математического выражения), а справа - ее числовое значение с единицей измерения. Например: t=1O°C.

При табличной записи множества результатов единицу измерения записывают один раз, рядом с наименованием измеряемой величи­ны.

Для функций вида y=f(x) - графически в виде непрерывных и то­чечных кривых (диаграмм). Обеспечивает большую наглядность.

Математические действия над результатами измерений

При математических действиях над результатами измерений нуж­но учитывать, что они (результаты измерения) являются случайны­ми значениями измеренных величин.

Допустим, что при проведении n измерений, результат Q был по­лучен с вероятностью Р (График 1);

Тогда при умножении его на постоянное число и при возведении в квадрат (действия с одним результатом измерения) получим кривые распределения его вероятности 2 и 3 соответственно.

При сложении одинаковых результатов и их перемножении (дейст­вия с двумя результатами измерения) результат получится несколь­ко иным (кривые 4 и 5):

Таким образом, простейшие математические действия над резуль­татами измерения приводят к трансформации его закона распреде­ления.

Факторы, влияющие на результат измерений.

Многообразие факторов, влияющих на результат измерения, можно поделить на внешние и внутренние, случайные и неслучайные и т.д. Их действие проявляется в рассеянии результата измерения (при повторении измерительной процедуры или одновременном выпол­нении ее несколькими средствами измерений и (или) разными ме­тодами) и смещении центра рассеяния относительно значения из­меряемого размера.

Исключение, компенсация и учет влияющих факторов осущест­вляются на этапах подготовки и выполнения измерений, обработки экспериментальных данных и представления результатов измере­ний.