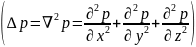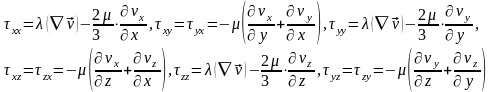- •1.Снарядтың ұшу траекториясын бірінші ретті дифференциалдық теңдеулер жүйесімен берілген Коши есебімен модельдеу.
- •2.Гармониялық тербелістің фазалық жазықтағы сипаттамасын математикалық модельдеу.
- •3.Математикалық маятниктің тербелісін модельдеу.
- •4.Ферхюльстің математикалық моделі.
- •5.“Жыртқыш-Жемтік” математикалық моделі.
- •6.Вольтерр-Лотка теңдеуінің фазалық жазықтықтағы сипаттамасы.
- •7.“Жыртқыш-Жемтік” математикалық моделінің кинематикалық сипаттамасы.
- •8.Көптүйіліскен аймақ үшін сығылмайтын сұйықтың фильтірлену есебінің математикалық моделі.
- •9.Мятиев -Гиринский математикалық моделін қорыту және механикалық мағанасы.
- •10.Хантуш математикалық моделін қорыту және механикалық мағанасы.
- •9) Ракетаның ұшу траекториясын бірінші ретті дифференциалдық теңдеулер жүйесімен берілген Коши есебімен модельдеу.
- •11.Толық электрлік тізбектің математикалық моделі
- •13)Тұтқырлық үйкеліс күштің әсеріне байланысты тербелісті модельдеу.
- •§2. Қозғалыс теңдеуін Ньютонның тұтқырлық заңын ескеріп жазу.
- •14)Тербелісті сипаттайтын модельдің Эйлер сандық шешімі.
- •20)Келтірілген пластық қысымға түсінік.
- •24. Сығылмайтын сұйықтың фильтірлену математикалық моделінің Пуассон теңдеуі және дельта функцияның сипаттамасы.
- •26. Мятиев-Гиринский математикалық модельнің сандық шешімінің интегралдық баланыс теңдеуін қорыту және механикалық мағанасы.
- •Дарси заңы:
- •Флюид күйін сипаттайтын теңдеу:
- •Кеуек орта:
- •27.Тұтқырлы пластикалық сұйықтың фильтірлену жылдамдығының математикалық моделі.
- •28.Тұтқырлы пластикалық сұйықтың фильтірлену пьезоөткізгіштік математикалық моделі.
- •31.Ньютондық емес сұйықтың фильтірлену жылдамдығының математикалық моделін қорыту.
- •31.Ньютондық емес сұйықтың фильтірлену жылдамдығының математикалық моделін қорыту.
- •32. Ньютондық емес сұйықтың фильтірлену пьезоөткізгіштік математикалық моделі
- •33. Ньютондық емес сұйықтың тұтқырлықтары әртүрлі қозғалыстағы ағынға байланысты жылжымалы шекарасын модельдеу.
- •34. Ньютондық емес сұйықтың фильтірлену жылдамдығының сызбасы және механикалық мағанасы.
- •35. Сұйықтың негізгі модельдері.
- •36.Уақыт бойынша туындыларды айыру және механикалық мағанасы.
- •37.Скалярлық және векторлық шамалардың субстанциалық туындылары.
- •38.Үзіліссіздік теңдеудің механикалық мағанасы және моделін қорыту.
- •40.Қозғалыс мөлшерін математикалық модельдеу және механикалық мағанасы.
- •41.Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпатын модельдеу
- •41.Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпатын модельдеу.
- •42. Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпаты және механикалық мағанасы.
- •43.Ньютондық тұтқырлық заңының декарт координат жүйесіндегі формулалары.
13)Тұтқырлық үйкеліс күштің әсеріне байланысты тербелісті модельдеу.
Субстанциялық туындысы бойынша берілген қозғалыс теңдеуі.
Қозғалыс теңдеуінің векторлық жазбасы.
(2 (3) (4) (5)

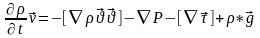 (1)
(1)
 =0
(2)
=0
(2)
1 – Бірлік көлемдегі қозғалыс мөлшерініңайналу жылдамдығы.
2 – Бірлік көлемдегі конвенциялық тасымалдану әсерінен қозғалыс мөлшерінің жиналу жылдамдығы.
3 – Бірлік көлемге шағылған қысым күші.
4 - Бірлік көлемдегі тұтқырлық күштің (яғни жылдамдықтар градиенті) тасымалдану әсеріне байланысты қозғалыс мөлшерінің тасымалдану жылдамдығы.
- ші теңдеудегі (2) және (4), яғни [
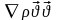 ]
және [
]
және [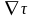 ]
тензорлық табиғатына байланысты
дивергенциялық
амалдарды қарастыруға болмайды.
]
тензорлық табиғатына байланысты
дивергенциялық
амалдарды қарастыруға болмайды.
Қозғалыс мөлшерінің х компоненттеріне тәуелді қосындысына келесі амалды қолданайық.
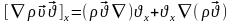
Бірлік
көлемдегі массаның сақталу балансы: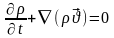 (3)
(3)
– ші теңдеуді қозғалыс мөлшерінің х компоненті бойынша алайық.
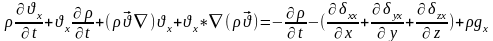 ,
,
(2)-ші теңдікті ескеріп:
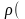
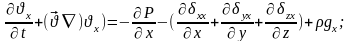
Немесе
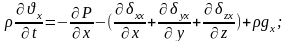

х - құраушысы бойынша субстанциялық туынды.
Субстанциялық туындысы қалған у және z - құраушылары бойынша:
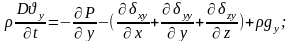
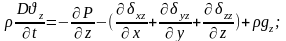
Жалпы векторлық жазбасы:
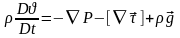 (4)
(4)
(2) (3) (4)
1 – Бірлік көлемнің массасына көбейтілген үдеу.
2 – Бірлік көлемге шағылған қысым күші.
3 – Бірлік көлемге шағылған тұтқырлық үйкеліс күш.
4 – Бірлік көлемге шағылған ауырлық күш.
–ші теңдеуді Ньютонның 2-ші заңын ескеріп тұжырымдасақ сұйықпен бірге қозғалған бірлік көлемдік элементке әсер еткен күштердің нәтижесінде алған үдеумен
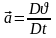 қозғалысы масса*үдеу=күштер қысымы.
қозғалысы масса*үдеу=күштер қысымы.
§2. Қозғалыс теңдеуін Ньютонның тұтқырлық заңын ескеріп жазу.
Қозғалыс теңдеуін жылдамдықтардың осьтердегі компонентерін ескеріп жазу үшін Ньютондық сұйықтық кернеулермен нормаль және тангенциалды жылдамдық градиенті араларындағы байланысты жазайық. Нормальдің бойымен бағытталан кернеулер:
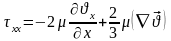 ,
,
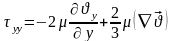 ,
,
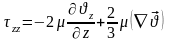 .
.
Тангенциалдық кернеулер:
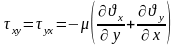 ,
,
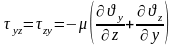 ,
,
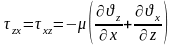 .
.
Сұйық
х осі бойынша қозғалса, онда
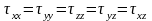 ,
осыдан
,
осыдан
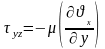 .
.
Бірлік өлшемдегі берілген Ньютонның тұтқырлық заңы шығады.
– ші теңдіктерді ескеріп, тұтқырлығы және тығыздығы айнымалы болғандағы Ньютонның сұйықтық қозғалыс теңдеуін аламыз:
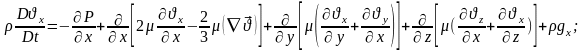
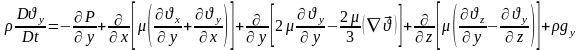
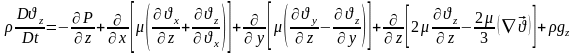
14)Тербелісті сипаттайтын модельдің Эйлер сандық шешімі.
Эйлердің қозғалыс теңдеуі (1775ж)(Идеал сұйық)
Идеалдық
сұйық үшін элементтік көлемге әсер
ететін кернеу векторы τ элемент бетіне
түсірілген
 нормалдың бойымен әсер етеді, яғни
тангенциалдық кернеу векторы нольге
тең. Сөйтіп тұтқырлық күшке байланысты
нормалдың бойымен әсер етеді, яғни
тангенциалдық кернеу векторы нольге
тең. Сөйтіп тұтқырлық күшке байланысты
(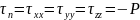 )
тасымалдау болмайды.
)
тасымалдау болмайды.
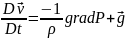
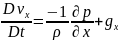
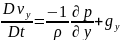


15)Кеуек ортаның күйін сипаттайтын теңдеу.Кеуектілік. Сұйықтар мен газдардың кеуек ортадан фильтрленуі өзара қосылған қуыс жолдармен жүреді. Сондықтан кеуек ортаның барлық сипаттамасы осы кеуекті (өзара байланысқан қуыс) кеңістікпен беріледі.
Тау
жынысына байланысты пласт-қабаттан
ойша көлем алайық. Мұндағы өзара байланысқан
кеуек ортаның көлемі
көлем алайық. Мұндағы өзара байланысқан
кеуек ортаның көлемі
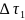 болсын, онда кеуек ортаның сипаттамасы
ретінде орташа кеуектілік
болсын, онда кеуек ортаның сипаттамасы
ретінде орташа кеуектілік
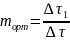 немесе толық орташа кеуектілік алынады.
немесе толық орташа кеуектілік алынады.
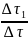

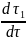
1- сурет. Кеуектіліктің өзгерісінің қисығы.
Осыдан тұтас ортаға көшу үшін көлемді осы элемент ішіндегі бір нүктеге дейін қысамыз. Кеуектіліктің орташа мәні басында бірқалыпты баяу өзгерсе (себебі қуыс ортадан барынша көп), артынан көлемді қысқан сайын қатынастың өзгерісі секірмелі болады (сур. 1). Орташа кеуектілікпен көлем арасындағы бірқалыпты байланысты бөлігін нөлге дейін экстрополяциаласақ тұтас емес ортадан тұтас ортаға, немесе аз шамалардың қатынасынан туындыға көшеміз
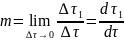 .
.
Жерасты гидродинамикасында кеуектілік коэффициент ұғымы ретінде өзара қосылған микрожарықшақтарды және кеуек орталардағы сұйықтардың қозғалысы жүретін активті қуыс кеңістік қарасытырылады.
Саңылау
коэффициенті n
деп кеуек ортаның қимасы бойынша алынған
саңлаулар ауданының
 осы қиманың барлық ауданына
осы қиманың барлық ауданына
 қатынасын айтады
қатынасын айтады
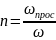 .
.
Пласт-қабаттың орташа ұзындығы бойынша алынған саңлаулар шамасы кеуектілікті береді
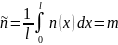 ,
,
сондықтан
саңлаулар ауданының орташа мәні
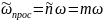 .
.
Кеуек
ортаның
қарапайым моделі ретінде жалған жердің
моделі алынады. Жалған жер диаметрі
бірдей шариктерден құрастырылып, нақтылы
түрде жинастырылады. Жалған жердің
сегіз өзара түйіліскен бөлшектерінің
центрі бұрыштардың шыңы болса негізгі
элементі (негізігі ұяшық) ромбоэдр
болады. Ромбоэдрдің бүйір қырының сүйір
бұрышына байланысты жинастырылған
шарлардың тығыздығы өзгереді. Мысалы
бұрыш
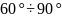 өзгерсе, онда
өзгерсе, онда
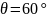 шарлардың тығыз орналасуына сәйкес, ал
шарлардың тығыз орналасуына сәйкес, ал
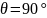 шарлар кең орналасып, тығыздығы аз
болады.
шарлар кең орналасып, тығыздығы аз
болады.
16)Әлсіз
сығылатын сұйықтың күйін сипаттайтын
теңдеу.Cығылмайтын сұйық үшін Ньютонның
жалпыланған тұтқырлық заңыI.Ньютонынң
тұтқырлық заңы: сұйықтардың ағысын
сипаттауға байланысты.Сұйықтар:ньютондық
және ньютондық емес болып бөлінеді.Бір
пластинаны қарастырайық, ішінде ньютондық
сұйық үшін ағыс болсын.Сонда
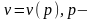 кез
келген нүктеде, болса ағыс ламинар, ал
егер
кез
келген нүктеде, болса ағыс ламинар, ал
егер
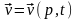 болса
стационар ағыс болады.
болса
стационар ағыс болады.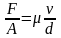 қатынасы орындалады, мұндағы
қатынасы орындалады, мұндағы
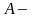 аудан,
аудан,
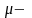 сұйықтың
тұтқырлық коэффициенті. Бұдан ламинар
сұйықтарға арналған Ньютонның тұтқырлық
заңын аламыз:
сұйықтың
тұтқырлық коэффициенті. Бұдан ламинар
сұйықтарға арналған Ньютонның тұтқырлық
заңын аламыз: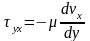 ,
мұнда азаюы бағытына қарай алғынымыздан
минус таңбасын қойдық.
,
мұнда азаюы бағытына қарай алғынымыздан
минус таңбасын қойдық.
II.
Ньютонның жалпыланған тұтқырлық заңы.
Мұнда сұйық ішінен кез келген векторлық
ағынды аламыз:
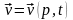 .
Енді ойша куб көлем аламыз:
.
Енді ойша куб көлем аламыз:
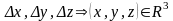 .
Кейін нормаль аламыз, сонда оның кернеуі:
.
Кейін нормаль аламыз, сонда оның кернеуі:
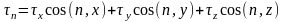 .Енді
осыны тензор түрінде жазсақ:
.Енді
осыны тензор түрінде жазсақ:
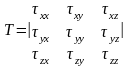 (1)-кернеу
тензоры.
(1)-кернеу
тензоры.
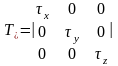 (2)- кернеу тензорын нормаль бойымен
бағытталған өзара перпендикуляр кернеу
күштерге жіктеуге болады.
(2)- кернеу тензорын нормаль бойымен
бағытталған өзара перпендикуляр кернеу
күштерге жіктеуге болады.
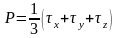 (3)-
теріс таңбамен,нормаль бойымен алынған
кернеу күштерінің арифм.қосындысы
кернеу күшін береді.
(3)-
теріс таңбамен,нормаль бойымен алынған
кернеу күштерінің арифм.қосындысы
кернеу күшін береді.
Мұндағы:
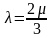 ,
егер
,
егер
 сығылатын
сұйық болса,
сығылатын
сұйық болса,
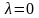 ,
егер
,
егер
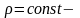 сығылмайтын сұйық болса.
сығылмайтын сұйық болса.
17)Кеуек
орта үшін фильтірлену Дарси заңы.Бірінші
рет кеуек ортаға байланысты сұйықтың
фильтрлену заңдылығын француз инженері
Анри Флибер Гаспар Дарси (фр.Henry Philibert
Gaspard Dapcy 1803-1858, Париж) зерттеді. Дижон
қаласын сумен қамтамасыз ету үшін
тәжрибе жасады (2 сурет). Вертикаль труба
бойынша торға құм толтырып су жібереді.
Трубаға орналастырылған крандар арқылы
судың мөлшерін байқап манометрмен
қысымның
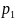 және
және
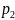 шамаларын біліп отырады.
шамаларын біліп отырады.
Дарси бұл тәжрибенің нәтижесін келесі теңдеумен береді
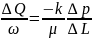 ,
(1)
,
(1)
мұнда,
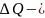 шығын
шығын
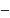 бірлік уақытта
қима арқылы ағатын сұйық көлемі;
бірлік уақытта
қима арқылы ағатын сұйық көлемі;
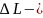 ұзындық;
ұзындық;
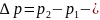 сұйық шығатын және енетін жерге байланысты
қысым айрымы.
сұйық шығатын және енетін жерге байланысты
қысым айрымы.

2 сурет. Дарсидың приборы.
(1)-ші теңдеудің сол жағы сұйықтың фильтрлену жылдамдығы
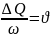
Флюид
(сұйық не газ) қозғалысының орташа
жылдамдығы
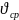 көлемдік шығынның саңлаулар ауданына
көлемдік шығынның саңлаулар ауданына
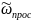 қатынасы
қатынасы
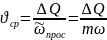 .
.
Сөйтіп
фильтрлік жылдамдықтан кеуек ортадағы
флюидтің қозғалысының орташа жылдамдығына
кеуектілік коэффициенті арқылы көшеді
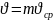 .
.
Үшөлшемді изотроптық пласт-қабаттың, яғни барлық бағыттағы қасиеттері бірдей болса, фильтрлену жылдамдығы келесі формулалармен табылады
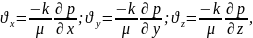 (2)
(2)
Үш
проекциясы бойынша берілген шама, үш
өзара перпендикуляр бағыттағы жылдамдықтың
өзгерісін анықтайды. Бірлік
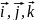 векторлардың көмегімен жылдамдықты
векторлық теңдеумен берейік
векторлардың көмегімен жылдамдықты
векторлық теңдеумен берейік
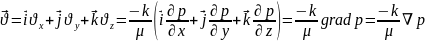 .
(3)
.
(3)
Сөйтіп Дарси заңы фильтрлік жылдамдықтың (2) және (3) қысым градиентіне сызықты байланысты болатынын көрсетті. Мұнай өндіру механикасында негізінен Дарси заңы кеңінен қолданылады. Жоғарғы жылдамдықтарда Дарси заңы орындалмайды (ұңғыма маңайындағы зона).
Өтімділіктің өлшем бірлігін (2) формуладан шығарайық
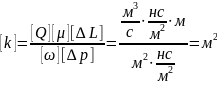 .
Сұйықтың фильтрлік қозғалысы үшін
инерттік күш ескерілмесе Дарси
заңы
(3) бойынша параметрлердің ішінде тығыздық
шамасының әсері болмайды, себебі
сұйықтың қозғалысы баяу болады.
.
Сұйықтың фильтрлік қозғалысы үшін
инерттік күш ескерілмесе Дарси
заңы
(3) бойынша параметрлердің ішінде тығыздық
шамасының әсері болмайды, себебі
сұйықтың қозғалысы баяу болады.
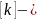 өлшемі аудан өлшембірілгімен бірдей
немесе Халықаралық жүйе
өлшемі аудан өлшембірілгімен бірдей
немесе Халықаралық жүйе
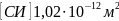 бірлік бойынша бір Дарси (Д) деп аталады,
сөйтіп кеуек ортаның геометриялық
сипаттамасы болып, сұйықтың қасиетін
бермейді. Өтімділіктің өлшембірлігі 1
Д –деп, егер ауданы
бірлік бойынша бір Дарси (Д) деп аталады,
сөйтіп кеуек ортаның геометриялық
сипаттамасы болып, сұйықтың қасиетін
бермейді. Өтімділіктің өлшембірлігі 1
Д –деп, егер ауданы
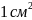 ұзындығы
ұзындығы
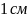 үлгіге түскен қысым шамасы
үлгіге түскен қысым шамасы
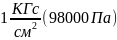 болғанда, сұйықтың тұтқырлығы
болғанда, сұйықтың тұтқырлығы
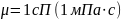 үшін сұйық шығынның шамасы
үшін сұйық шығынның шамасы
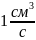 болса.
болса.
Дарси заңы орындалмаған жағдайда кеуек ортадағы сұйық қозғалысының жылдамдығы мен қысым градиентінің арасындағы байланысты екі мүшеден тұратын формуламен береді [1]
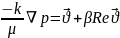 .
(4)
.
(4)
Мұнда
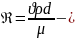 Рейнольдс саны
Рейнольдс саны
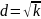 ;
;
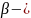 кейбір
кеуек орта үшін тұрақты шама. Екі мүшелік
фильтрлік заңын бірінші рет ұсынған
Форхгеймер және бұл формула Рейнольдс
санының үлкен мәндерінде де сұйықтың
кеуек ортадағы қозғалысын бере алады.
кейбір
кеуек орта үшін тұрақты шама. Екі мүшелік
фильтрлік заңын бірінші рет ұсынған
Форхгеймер және бұл формула Рейнольдс
санының үлкен мәндерінде де сұйықтың
кеуек ортадағы қозғалысын бере алады.
18)Флюид
массасының үзілісіздік заңын қорыту.Флюид
массасына көшейік. Параллелепипедтегі
кеуек қуыс көлем шамасы
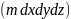 ,
ал масса шамасы
,
ал масса шамасы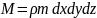 , m-элементар
, m-элементар
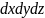 көлемнің куектілігі.
көлемнің куектілігі.
Осыдан параллелепипедтің кеуек көлемінде жиналған масса шамасы
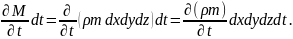 (2)
(2)
Флюид
массасының сақталу баланысы бойынша
(1) және (2) өзара теңестіріп және
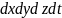 қысқартып үзіліссіздік
теңдеуін
аламыз
қысқартып үзіліссіздік
теңдеуін
аламыз
 (3)
(3)
Теңдеудің
сол жағы массалық
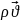 жылдамдықтың дивергенциясы болғандықтан
(3)
келесі түрде
жазылады
жылдамдықтың дивергенциясы болғандықтан
(3)
келесі түрде
жазылады
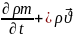 =0.
=0.
2. Үзіліссіздік теңдеуін Остраградский-Гаусс формуласын қолданып жалпы әдіспен қортуға болады. Ойша алынған көлем ішіндегі кеуек-қуыстағы флюид массасының өзгерісі бірлік уақыттағы флюид тығыздығының өзгерісін тудырады, яғни
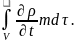
Массаның
сақталу заңы бойынша бірлік уақытта
кеуек-қуыстағы флюид массасының жиналуы
осы көлем шектелген
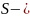 беттен өтетін массалық жылдамдықтың
ағынына тура байланысты
беттен өтетін массалық жылдамдықтың
ағынына тура байланысты
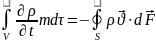 .
.
мұнда
бетке түсірілген бірлік вектор массалық
жылдамдықтың азаю жағына бағытталған,
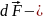 элементар
ауданша вектормен
элементар
ауданша вектормен
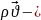 массалық жылдамдықтың скалярлық
көбейтіндісі.
массалық жылдамдықтың скалярлық
көбейтіндісі.
19)Пьезоөткеізгіштік теңдеуінің моделін қорыту.Пьезоөткізгіштік теңдеуді қорытудың жалпы әдісін Остраградский-Гаусс формуласын қолданып қортайық. Кеуек ортада алынған элементар көлемдегі флюид массасының бірлік уақыттағы азаю шамасы
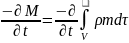 ,
(10)
,
(10)
екінші жағынан бұл азаюы көлем шектелген беттен аққан флюид масса жылдамдығының ағынымен анықталады
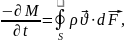
мұндағы
жылдамдық вектор
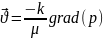 .
.
Флюид
мұнай болғанда күйін сипаттайтын теңдеу
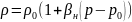
үшін
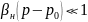 ,
яғни
,
яғни
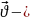 өзгерісі
барынша үлкен жылдамдықта жүреді, себебі
мұнай әлсіз сығылатын сұйық, ендеше
өзгерісі
барынша үлкен жылдамдықта жүреді, себебі
мұнай әлсіз сығылатын сұйық, ендеше
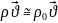 .
.
Осы көлем шектелген беттен өтетін толық масса ағыны тең
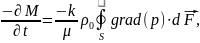 (11)
(11)
Флюид массасының баланысы орындалады, егер (10) және (11) теңестірсек.
Остраградский-Гаусстың теоремасы бойынша
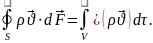
Осыдан
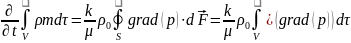
Серпімді кеуек ортаның флюидтің тығыздығына көбейтіндісі (5) теңдеудің негізінде
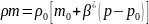 ,
,
мұнда
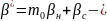 мұнай пласт-қабаттың серпімдік
сыйымдылығын сипаттайтын коэффициенті.
Біртекті сызықты пласт-қабаттағы
серпімді режимді сипаттайтын
соңғы
интегралды, тұрақты параметрлері үшін
мұнай пласт-қабаттың серпімдік
сыйымдылығын сипаттайтын коэффициенті.
Біртекті сызықты пласт-қабаттағы
серпімді режимді сипаттайтын
соңғы
интегралды, тұрақты параметрлері үшін
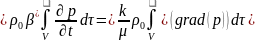 .
.
Интеграл астындағы өрнек екінші ретті параболалық теңдеуге жататын пьезоөткізгіштік теңдеуін береді. Лапластың операторын қолданып келесі түрде жазайық
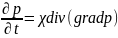 ,
(12)
,
(12)
мұнда
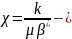 мұнай
пласт-қабаттың пьезоөткізгіштік
коэффициенті, ал
мұнай
пласт-қабаттың пьезоөткізгіштік
коэффициенті, ал
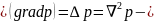 Лаплас
операторы
Лаплас
операторы