4.Ферхюльстің математикалық моделі.

Ферхюльст математикалық моделінде түсетін азықтың мөлшерін және биологиялық тіршіліктің азықты қолдану мүмкіндігін ескереміз.

1. Объекттің математикалық сипаттамасы

K=aN – b;

a – меншікті өсім

b – меншікті өлім

N=D-qx

q – тіршіліктің азықты қолдану мүмкіндігі

D – бар азық мөлшері

K=a(D – qx) – b =aD-b-aqx

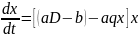(1)

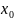x(0)= (2)

C=aD – b , егер a>b, онда C – эффектілік өсім.

2. Математикалық модельді зерттеу

эффектілік өсім бойынша 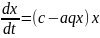теңдеуі сызықты емес, осы теңдеуді сызықтандыру жасаймыз.

;

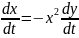(3)

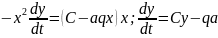
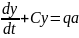(4)

(4) – сызықтандырылған Ферхюльст теңдеуі.

Екі жағдай қарастырайық: C=0 және C≠0.

1. C=0 (aD=b).

( 4) теңдеуінің шешімі y(t)= aqt + B; y(0)=B; B= ;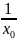

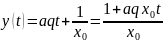(5)

(5) – сызықты түрдегі (4) теңдеудің шешімі.

2. C≠0.

(4) теңдеуді көбейтеміз 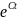-ға

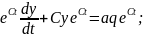бұдан

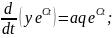
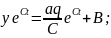
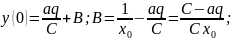осыны жалпы шешімге қоямыз:

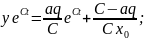
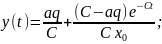
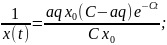
Ферхюльст теңдеуінің шешімі

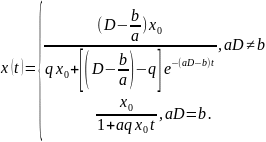(6)

C=0 (aD=b) – тепе теңдік жағдай.

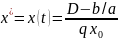; (7)

(7) – теңдік биологиялық өмір сүру тепетеңдігі.

1. ,(aD>b) біртіндеп өзінің тепетеңдік жағдайына келеді

2. 

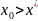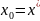
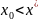3. ,(aD>b) біртіндеп өзінің тепетеңдік жағдайына келеді

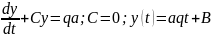
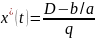
t-ға байл.өзгермейді

3. Мат. модельді интерпретациялау

5.“Жыртқыш-Жемтік” математикалық моделі.

Екі түрдің теңдеулері: x₁=x₁(t)-жемтік; x₂=x₂(t)-жыртқыш

1. Егер жемтіктің азығы шектелмеген және жыртқыш жоқ болса жемтік өседі:

x₁(t)=kx₁(t); x₁(0)=x₁₀

x₁(t)=x₁₀exp(xt); k₁=ε_1, мұндағы k₁ -табиғи өсім

2. Егер жемтік жоқ болса

ẋ₂(t)= -ε₂x₂(t); x₂(0)=x₂₀

x₂(t)=x₂₀exp(-ε₂t)

Екібиологиялықтіршілікшектелгенаймақтаөмірсүргендебір-бірінеәсеріайтарлықтайболады. Әринежемтіктіңөсімсаны, жыртқыштыңжалпысаныөскенсайын, азаябереді. Екіншіжағынанжемтіктіңсаныазайғансайын, жыртқыштыңөсімікөбейеді, себебіжыртқыштыңқорегіөседі. Нәтижесінмынадайдифференциалдықтендеуменбереміз

I k₁=ε₁-γ₁x₂(t) ẋ₁(t)=[ε₁-γ₁x₂(t)]

II k₂= -ε₂+γ₂x₁(t) ẋ₂(t)= -[ε₂- γ₂x₁(t)] ·x₂(t)

x₁(0)=x_10; x₂(0)=x₂₀

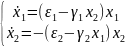(1)

Мұндағы коэффициенттер γ₁ және γ₂ жемтіктің және жыртқыштың өзара табиғи күресіне байланысты өсімінің өзгерісін сипаттайды. Сөйтіп (1) теңдеу жүйесі өзіне сөйкес бастапқы шарттарымен "жыртқыш жемтік" деп аталатын белгілі математикалық модель болады.

Алынған модельге сапалық зерттеу жүргізу үшін айнымалыларды алмастырайық. Қарастырылатын шамаларды мынадай түрде анықтайық

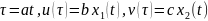,τ₁

ал a, b және с мәндері зерттелінетін тендеу қарапайым болатындай алынады. Жаңа айнымалылар негізінде, нәтижесін мынадай түрде жазайық

.

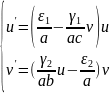
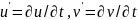Келесі параметрлерді анықтап

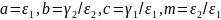, жүйені мынадай түрге келтіріп

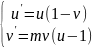(2),

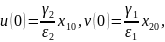
Вольтерра - Лотки теңдеуін аламыз. Жүйе (2) және (1) беретін мағынасы біреу. Анығында күй функдиялары u, v және тәуелсіз айнымалы t уақыт, сәйкес ескі шамалардан x₁, х₂ және t айырмашылығы тұрақты көбейткіштерімен анықталады.

Сапалық анализ жасаймыз. Динамикалық жүйенің тепе-теңдік жағдайы.

I. u=0, v=0 – тривиалды жағдай. Биологиялық тіршілік жоқ.

II. Тривиалды емес жағдай u=1, v=1 динамикалық жүйе өмір сүреді осы тепе-теңдік жүйенің маңайында өтеді.