
- •1.Снарядтың ұшу траекториясын бірінші ретті дифференциалдық теңдеулер жүйесімен берілген Коши есебімен модельдеу.
- •2.Гармониялық тербелістің фазалық жазықтағы сипаттамасын математикалық модельдеу.
- •3.Математикалық маятниктің тербелісін модельдеу.
- •4.Ферхюльстің математикалық моделі.
- •5.“Жыртқыш-Жемтік” математикалық моделі.
- •6.Вольтерр-Лотка теңдеуінің фазалық жазықтықтағы сипаттамасы.
- •7.“Жыртқыш-Жемтік” математикалық моделінің кинематикалық сипаттамасы.
- •8.Көптүйіліскен аймақ үшін сығылмайтын сұйықтың фильтірлену есебінің математикалық моделі.
- •9.Мятиев -Гиринский математикалық моделін қорыту және механикалық мағанасы.
- •10.Хантуш математикалық моделін қорыту және механикалық мағанасы.
- •9) Ракетаның ұшу траекториясын бірінші ретті дифференциалдық теңдеулер жүйесімен берілген Коши есебімен модельдеу.
- •11.Толық электрлік тізбектің математикалық моделі
- •13)Тұтқырлық үйкеліс күштің әсеріне байланысты тербелісті модельдеу.
- •§2. Қозғалыс теңдеуін Ньютонның тұтқырлық заңын ескеріп жазу.
- •14)Тербелісті сипаттайтын модельдің Эйлер сандық шешімі.
- •20)Келтірілген пластық қысымға түсінік.
- •24. Сығылмайтын сұйықтың фильтірлену математикалық моделінің Пуассон теңдеуі және дельта функцияның сипаттамасы.
- •26. Мятиев-Гиринский математикалық модельнің сандық шешімінің интегралдық баланыс теңдеуін қорыту және механикалық мағанасы.
- •Дарси заңы:
- •Флюид күйін сипаттайтын теңдеу:
- •Кеуек орта:
- •27.Тұтқырлы пластикалық сұйықтың фильтірлену жылдамдығының математикалық моделі.
- •28.Тұтқырлы пластикалық сұйықтың фильтірлену пьезоөткізгіштік математикалық моделі.
- •31.Ньютондық емес сұйықтың фильтірлену жылдамдығының математикалық моделін қорыту.
- •31.Ньютондық емес сұйықтың фильтірлену жылдамдығының математикалық моделін қорыту.
- •32. Ньютондық емес сұйықтың фильтірлену пьезоөткізгіштік математикалық моделі
- •33. Ньютондық емес сұйықтың тұтқырлықтары әртүрлі қозғалыстағы ағынға байланысты жылжымалы шекарасын модельдеу.
- •34. Ньютондық емес сұйықтың фильтірлену жылдамдығының сызбасы және механикалық мағанасы.
- •35. Сұйықтың негізгі модельдері.
- •36.Уақыт бойынша туындыларды айыру және механикалық мағанасы.
- •37.Скалярлық және векторлық шамалардың субстанциалық туындылары.
- •38.Үзіліссіздік теңдеудің механикалық мағанасы және моделін қорыту.
- •40.Қозғалыс мөлшерін математикалық модельдеу және механикалық мағанасы.
- •41.Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпатын модельдеу
- •41.Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпатын модельдеу.
- •42. Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпаты және механикалық мағанасы.
- •43.Ньютондық тұтқырлық заңының декарт координат жүйесіндегі формулалары.
41.Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпатын модельдеу.
Тұтас механикалық орта векторлық өрістен тұрсын.Ойша қабырғалары dxdydz болатын элементар көлем аламыз.

Қозғалыс
теңдеуінің балансы элементар көлемдегі
қозғалыс мөлшерінің жиналу жылдамдығы
былай анықталады.Эл.көлемдегі қ.м-ң
жиналу жылдамдығы => Эл.көлемдегі енген
қ.м-ң өзгеру жылдамдығы + Эл.көлемдегі
шыққан қ.м-ң өзгеру жылдамдығы +Эл.көлемдегі
әсер ететін күштер жиыны.Қозғалыс
мөлшері 2 типке бөлінеді:1.Конвективтік
сипаттамасы;2.Молекулалық сипаттамасы.
Әсер ететін күштер жиыны қысымдық ж/е
ауырлық болып бөлінеді.OX :
dxdydz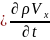 =(1)+(2)+(3)+(4)
=(1)+(2)+(3)+(4)
(1)Конвективті:
dydz(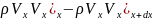 )+dxdz(
)+dxdz(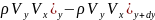 )+dxdy(
)+dxdy(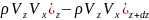 )
)
(2)Молекуляр:
dydz( )+dxdz(
)+dxdz(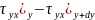 )+
dxdy(
)+
dxdy( )
)
(3)Қысымдық
күші: dydz(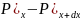 )+dxdz(
)+dxdz(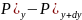 )+
dxdy(
)+
dxdy(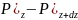 )
)
(4)Ауырлық
күші:
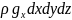
Тік
бұрышты координаталар жүйесінде.dxdydz=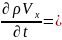 dydz(
)+dxdz(
)+
dxdy(
)+
dydz(
)+dxdz(
)+
dxdy(
)+
dydz(
)+dxdz(
)+
dxdy(
)+
dydz(
)+dxdz(
)+
dxdy(
)+
dydz(
)+dxdz(
)+
dxdy(
)+
dydz(
)+dxdz(
)+
dxdy(
)+
OX:
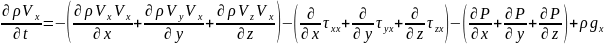
OY:
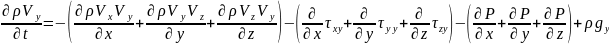
OZ:
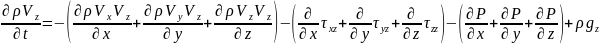
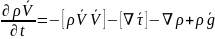
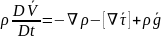
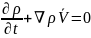 – Сұйық
ортаның массалық сақталу заңы.OX
бойынша тензорды набла операторын
пайдаланып жазамыз
– Сұйық
ортаның массалық сақталу заңы.OX
бойынша тензорды набла операторын
пайдаланып жазамыз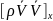 =(
=(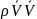 )
)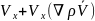
42. Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпаты және механикалық мағанасы.
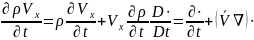
-субстанциалдық туынды бойынша
X
oсі бойынша:
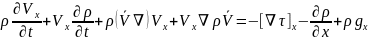
Y
осі бойынша: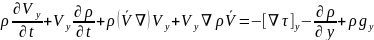
Z
осі бойынша: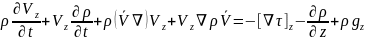
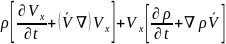 =
=
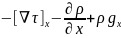
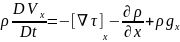
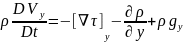
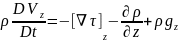
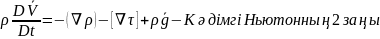 m
m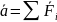 .
Механикалық мағынасы: қозғалыс теңдеуі
тензорлық жазбасы бекітілген координаталар
жүйесі үшін орындалады, субстанциалдық
жазбасы бекітілген координата жүйесі
н/е тұтас механикалық координата
жүйесімен бірге қозғалады.
=
.
Механикалық мағынасы: қозғалыс теңдеуі
тензорлық жазбасы бекітілген координаталар
жүйесі үшін орындалады, субстанциалдық
жазбасы бекітілген координата жүйесі
н/е тұтас механикалық координата
жүйесімен бірге қозғалады.
=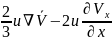
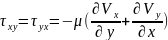
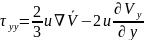
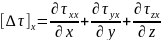
43.Ньютондық тұтқырлық заңының декарт координат жүйесіндегі формулалары.
Cығылмайтын сұйық үшін Ньютонның жалпыланған тұтқырлық заңы
I.Ньютонынң тұтқырлық заңы: сұйықтардың ағысын сипаттауға байланысты.Сұйықтар:ньютондық және ньютондық емес болып бөлінеді.
Бір пластинаны қарастырайық, ішінде ньютондық сұйық үшін ағыс болсын.Сонда кез келген нүктеде, болса ағыс ламинар, ал егер болса стационар ағыс болады. қатынасы орындалады, мұндағы аудан, сұйықтың тұтқырлық коэффициенті. Бұдан ламинар сұйықтарға арналған Ньютонның тұтқырлық заңын аламыз: , мұнда азаюы бағытына қарай алғынымыздан минус таңбасын қойдық.
II. Ньютонның жалпыланған тұтқырлық заңы. Мұнда сұйық ішінен кез келген векторлық ағынды аламыз: . Енді ойша куб көлем аламыз: . Кейін нормаль аламыз, сонда оның кернеуі:
.Енді осыны тензор түрінде жазсақ:
(1)-кернеу тензоры. (2)- кернеу тензорын нормаль бойымен бағытталған өзара перпендикуляр кернеу күштерге жіктеуге болады.
(3)- теріс таңбамен,нормаль бойымен алынған кернеу күштерінің арифм.қосындысы кернеу күшін береді.
Мұндағы: , егер сығылатын сұйық болса,
, егер сығылмайтын сұйық болса.
Сығылатын сұйық үшін жалпыланған Ньютонның тұтқырлық заңы
Н ьютонның тұтқырлық заңы: ағысын сипаттауға қолданылады
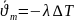
ср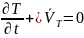
с
р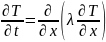
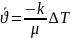
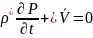
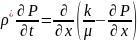
С
ұйық
үшін екі пластина алынды. 2 пластина
арасында Ньютондық сұйық берілсін. 1ші
пластина
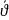 жылдамдықпен қозғалады.(2ge
bolip alindar grafikti)
жылдамдықпен қозғалады.(2ge
bolip alindar grafikti)
y
 y
y 
d
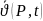
0 x сұйық су
1 пластина ламинарлы, стационарлы
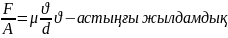
Ньютонның
тұтқырлық заңы
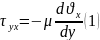
Ньютонның жалпыланған тұтқырлық заңы
P
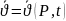 ойша куб көлем аламыз
ойша куб көлем аламыз
Декарт.коорд.
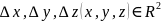
Кернеу
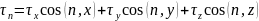
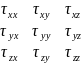 =T
(1) локалдық
кернеу күші
=T
(1) локалдық
кернеу күші
Кернеу тензорын нормаль бойымен бағытталған өзара 1 кернеу күштерге жетуге болады.
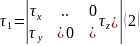
Куб
көлемге әсер етіп тұрған қысым күші :
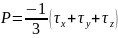 (3)
(3)
Теріс таңбамен алынған ,нормальдің бойымен алынған кернеу күштерінің қосындысының ортасы.
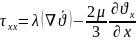 ;
;
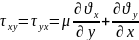
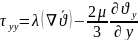 ;
;
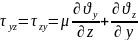
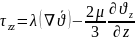 ;
;
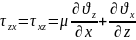
Жалпыланған
тұтқырлық заңы
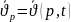 – сығылатын сұйық үшін
– сығылатын сұйық үшін
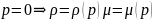
44.Сығылмайтын сұйықтың қозғалыс мөлшерінің Навье-Стокс математикалық моделі.\45-бирге\
45.Сығылмайтын сұйықтың қозғалыс мөлшерінің Навье-Стокс математикалық моделінің субстанциалық тұрпаты.\44-бирге\
Навье-Стокс теңдеуінің субстанциалдық түрінің векторлық жазбасы және механикалық мағынасы.
Гидродинамиканың толық теңдеуі тұтқырлықты сипаттайтын сұйық қабаттарының арасында пайда болатын үйкеліс күшін және бұған қосынша сыртқы күштердің әсерін, мысалы ауырлық күшін ескереді. Осылай алған қозғалыс теңдеуі кеңістік айнымалылары бойынша екінші ретті болады. Дебес жағдайда тұтқырлы сұйықтың қозғалысын зерттегенде сұйықтың тығыздығы тұрақты болады. Осыдан қозғалыс заңын және үзіліссіздік теңдеуін ескеріп Навье-Стокстың теңдеулер жүйесін жазайық.
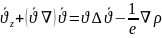
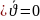
Субстанциалдық түрінің жазбасы
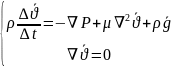 (1)
(1)
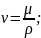
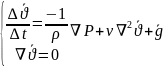 (2)
(2)
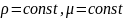
Ox бойынша:
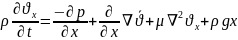
Oy
бойынша:
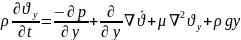
Oz
бойынша: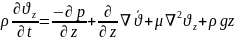
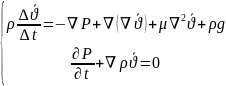 1822ж.
Навье-Стоксфрацузғалымы
тұтас механикалық орта үшін қозғалыс
теңдеуін сығылмайтын(ϸ=сonst,µ=const)келесі
түрде жазамыз.Тік бұрышты координата
жүйесінде ойша алынған элемент көлемінде
түсетін негізгі кернеу күштерді
нормальдың бойымен бағытталған деп
аламыз, ал қозғалыс теңдеуін тангенциалды
кернеу күштері бойынша жылдамдық
градиенттері арқылы өрнектеуді ұсынды
1822ж.
Навье-Стоксфрацузғалымы
тұтас механикалық орта үшін қозғалыс
теңдеуін сығылмайтын(ϸ=сonst,µ=const)келесі
түрде жазамыз.Тік бұрышты координата
жүйесінде ойша алынған элемент көлемінде
түсетін негізгі кернеу күштерді
нормальдың бойымен бағытталған деп
аламыз, ал қозғалыс теңдеуін тангенциалды
кернеу күштері бойынша жылдамдық
градиенттері арқылы өрнектеуді ұсынды
6)
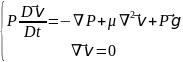
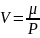 ;
-кинематикалық тұтқырлық коэфициенті
;
-кинематикалық тұтқырлық коэфициенті
7)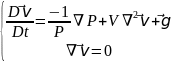
8)
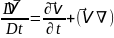 V⃗
субстанциалдық теңдеу
V⃗
субстанциалдық теңдеу
(6),(7) субстанциалдық теңдеулерді (8) бойынша ашып жазсақ онда Навье-Стокс теңдеуі бекітілген координатада орындалады.
Декарт коордита жүйесінде жазылуы:
Ox: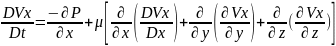 +:
𝒫𝚐x
+:
𝒫𝚐x
Oy:
𝒫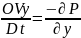 +
+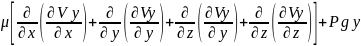
Oz:
𝒫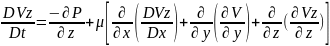 +
+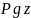
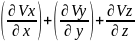 =0
=0
Механикалық мағынасы: Навье-Стокс теңдеулері сұйықты кез келген түрлері үшін орындалады, ал идеал сұйық үшінЭйлер қозғалыс теңдеуіне айналады.
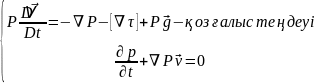
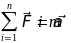
Ньютонның 2-ші заңынан алынады.
Енді кернеу тензорын ашайық:
𝒫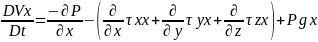
𝒫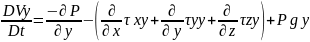
𝒫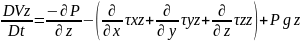
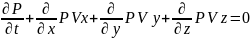 субстанциялдық
таңдеу
субстанциялдық
таңдеу
О𝑥 осі бойынша түрлендіру жасаймыз. Содан координаттар осьтері бойынша жазбасын аламыз:
Ox: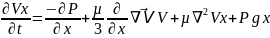
Oy:
𝒫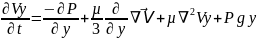
Oz:
𝒫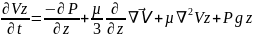
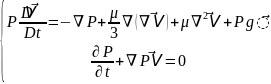 -Пуассон
қозғалыс теңдеуінің векторлы-тензорлық
жазбасы.
-Пуассон
қозғалыс теңдеуінің векторлы-тензорлық
жазбасы.
Механикалық мағынасы: Пуассон сығылатын сұйықтардың қозғалыс заңдылығын беретін теңдеу ,яғни Ньютондық сұйықтар, газдардың тұтас орта механикасының қозғалыс теңдеуін сипаттайды. Ньютондық емес үшін орындалмайды.
Навье-Стокс теңдеуінің субстанционалдық формасы ашылған векторлық жазбасы.
1822 ж Навье-Стокс (француз ғалымы). νСығылмайтын тұтас орта механикасы үшін =const, =const қозғалыс теңдеуін келесі түрде жазамызю Тікбұрышты координаттар жүйесінде ойша алынған элемент көлемге түсетін неізгі кернеу күштерді нормальдың бойымен бағытталған, ал қозғалыс теңдеуін тэнденианалдық кернеу күштері бойынша жылдамдық градиенті арқылы өрнектеуді ұсынды. Сығылмайтын сұйық үшін:
(1)
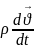 =
=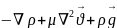
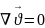
(1)-Навье-Стокс теңдеуі
 ;
;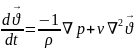 +
+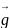 (2)
(2)
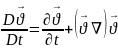 (3)
(3)
 еңдеулерді
субстанционалдық туынды (3)бойынша
ашып жазсақ, онда Навье-Стокс
теңдеуін бекітілген координаттар
жүйесінде аламыз.
еңдеулерді
субстанционалдық туынды (3)бойынша
ашып жазсақ, онда Навье-Стокс
теңдеуін бекітілген координаттар
жүйесінде аламыз.
46.Идеалдық сұйық үшін Эйлер математикалық моделі.\47-бирге\
47.Идеалдық сұйық үшін қозғалыс теңдеунің Эйлер математикалық моделінің субстанциалық жазбасы.\46-бирге\
Эйлер теңдеуінің векторлық жазбасы.
1755 ж Эйлер идеалды тұтас орта механикасы қозғалысы теңдеуін алды. Мұнда тенденционалдық кернеу күштері нормальдің бойымен әсер етеді де, нольге теңестіреді.
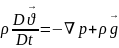 (1)
(1)
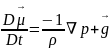
Эйлер теңдеуінің субстанционалдық формасы ашылған векторлық жазбасы.
1755 ж Эйлер идеалды тұтас орта механикасы қозғалысы теңдеуін алды. Мұнда тенденционалдық кернеу күштері нормальдің бойымен әсер етеді де, нольге теңестіреді.
(1)
Тік бұрышты координаттар жүйесінде субстанционалдық туынды бойынша:
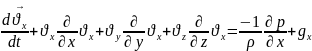
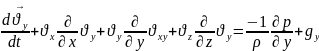
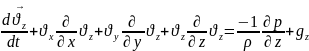
48.Тікбұрышты координаттар жүйесінде қозғалыс теңдеуін Х - кернеулер компоненттрі бойынша модельдеу.\49,50-бирге\
49.Тікбұрышты координаттар жүйесінде қозғалыс теңдеуін Y- кернеулер компоненттрі бойынша модельдеу.\48,50бирге\
50.Тікбұрышты координаттар жүйесінде қозғалыс теңдеуін Z- кернеулер компоненттрі бойынша модельдеу\48,49-бирге\
Қозғалыс теңдеуін қорыту
Тұтас механикалық орта векторлық өрістен тұрсын ойша қабырғалары dxdydz болатын элементар көлем аламыз.
 1-сурет
1-сурет
(1)сурет үшін қозғалыс теңдеуінің балансы элемен көлеміндегі қозғалыс мөлшерінің жиналу жылдамдығы қозғалыс мөлшері
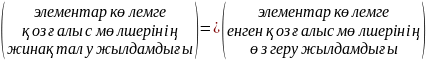 --
--
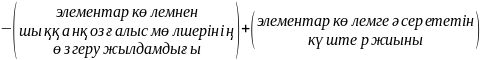
Қозғалыс мөлшері екі типке бөлінеді:
1.конвективтік сипаттамасы. (Көлемге байланысты)
2.мөлекулярлық сипаттамасы. (Жылдамдық градиенті тұтқырлық күш Ньютон)
Әсер ететін күштер жиыны қысымдық және ауырлық күштер болып бөлінеді.
Сурет ох осі бойынша dxdydz (1) –массалық жылдамдық
конитивтік
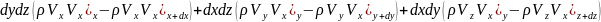
молекуляр:
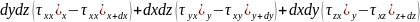
қысымдық:
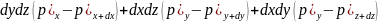
ауырлық күші:
тік бұрышты кооринаталар жүйесі Ох : dxdydz бөлеміз
dxdydz=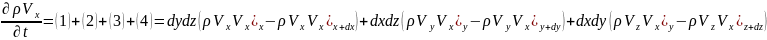 +
+
+
+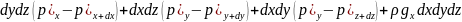 .
.
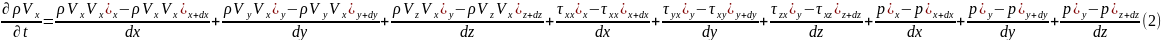
 (3)
(3)
Конвективтік сұйықтың көлемдік қозғалысы
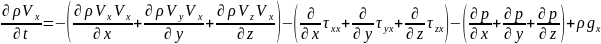
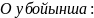
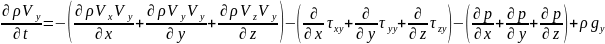
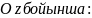
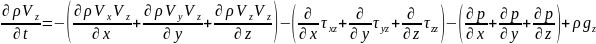 (4)
(4)
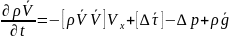 (5)
(5)
Ох бойытша тензор
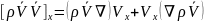 (6)
Сығылатын массалық сүйық ортаның сақталу
заңы
(6)
Сығылатын массалық сүйық ортаның сақталу
заңы
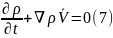
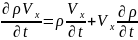 (8)
(8)
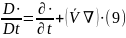 субстанциялдық
туытды бойынша
субстанциялдық
туытды бойынша
(6) Мен (8) ны топтастырып және (7) ы ескеріп
Х осі бойынша
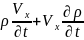 +
+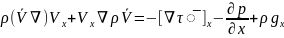
У осі бойынша
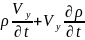 +
+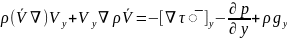
Zосі бойынша
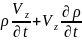 +
+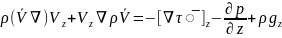
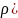 +
+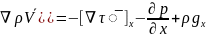 (10)
(10)
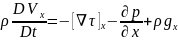
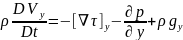
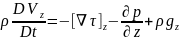 (11)
(11)
=> ρ
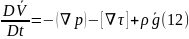 теңдеуі
Ньютонның екінші заңы боп табылады
теңдеуі
Ньютонның екінші заңы боп табылады
m (13).
Физикалық мағынасы
Жазбасы бекітілген координат жүйесі үшін орындалады. Ал қозғалыс теңдеуіның субстанциалдық жазбасы бекітілген координаталар жүйесі немесе тұтас механикалық орта координатасы жүйесімен бірге қозғалады.
